关于近代物理静电场学理论体系的思考
2018-04-14莫佳童
◎莫佳童
十九世纪,近代物理学即经典物理学在静电学研究方面取得了重要进展,一系列重要的相关研究和发现直接促进了电气化技术和工程上的新发展,致使第二次(电气化)工业革命的到来。时至今日,静电场学作为物理学研究的一个重要分支学科,在工程技术的发展及其国民经济领域发挥着重要的作用。本文通过对近代经典静电场学一系列理论的新思考,构建出关于静电场学的理论学术构架,这对于关于静电场学的学习、工程技术领域的应用以及物理学理论的进一步发展具有重要的价值意义。
一、静电场学及其研究对象
一般来讲,静电场学是研究相对静止电荷及其所形成电场的一门学科,是物理学的重要分支学科之一。它的研究对象主要是相对静止的点电荷周围的电场以及放入其中的物体。一般主流学术观点认为,静电场是电荷周围空间存在的一种特殊形态的物质,能够对置于其中的电荷等物体有力的作用,是与分子原子结构大不相同的一种客观存在的物质。
二、关于近代经典静电场学理论的构建
1.静电场力学模型的构建 研究静电场学一般先从电荷开始研究。电荷不是特定的物质,它是带电粒子的统称。大量实验发现,电荷间存在引力和斥力两种情况,十八世纪,科学家富兰克林针对这种情况首先提出电荷分为两种这一学说,后来库仑在富兰克林的基础上总结出电荷分为正负两种。再后来人们规定:丝绸摩擦的玻璃棒带正电,毛皮摩擦的橡胶棒带负电,即“同种电荷相互排斥,异种电荷相互吸引”。由此可见,力学和电学密不可分,所以在静电学方面的的研究自然的要从力学开始突破。十九世纪,科学家库仑借鉴了万有引力理论,通过扭秤实验测量和分析,初步判定这个力的大小与两电荷量的乘积成正比及它们之间的距离存在平方反比关系。式子1所示的就是库仑定律。这个理论目前被普遍接受,后来就是用库仑C作为电荷量的单位。
在牛顿力学思想影响下,力的存在不能脱离物体,那么电荷周围就必然存在一种特殊物质,由此我们认为电荷周围必定存在电场。电场十分抽象,为了方便研究,我们引入了电场强度这个物理量——E。从数学角度定义了式子2,这个公式适用于一切电场。如果把库仑定律公式带入,则得出式子3,此公式适用于真空中点电荷周围的电场,且为决定式。上述公式中电场强度是矢量——运算遵循平行四边形定则,电荷量数据不带入正负号。为了客观描述电场,我们引入“电场线”,电场线是一个假想的不闭合曲线,由正电荷指向负方向相反),科学家高斯在这方面做出了阐述,后人称之为高斯定理,如式子4。这样,我们就可以用力学观点描述电荷间、电场与电荷之间的受力问题。

2.静电场运动学模型的构建 电荷间存在力的作用,就必然可以致使运动。根据牛顿运动定律F=ma,则我们可以推导出静电场力的加速度a,如式5,继而产生各种直线和曲线运动情况。常见的运动有匀速直线运动、匀变速直线运动、类平抛运动、圆周运动以及复杂的曲线运动。力和运动永远密不可分,再复杂的曲线运动,合外力都由轨迹的凹侧指向外,对照合外力的大致方向与电场线方向可确定物体的电性,其它问题迎刃而解。这样可以应用运动学的理论观点分析电荷的运动问题。
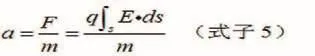
3.静电场功能理论构建 由于物体在电场中运动,那么库仑力就可以对它做功。功是能量转化的量度,这样从“能”的角度引入了“电势能”这个物理量。电势能是指电荷在电场中由于受电场作用而具有有位置决定的能量(引入)。与重力势能类似,如式子6所示,W=-Ep变化量,电势能大小的确定也需要规定一个零势能面,这个势能面所具有能量的标度称为电势,如式子7所示。电场线方向是电势降落最快的方向。电势是电场中物体具有的电势能与其所带电荷量的比(q在这个标量式中须代入正负号)。电荷运动过程中电势可能变化,这时就需要一个新物理量电势差U来化简复杂的运动过程。U=初电势-末电势,如式子8,与变化率不同。所以,W=-Ep变化量=Ep初-Ep末=q(初电势-末电势)=qU。科学家安培总结了静电场的功能关系,电荷在静电场运动轨迹为闭合曲线时,电场力做功为零,即后来我们所说的安培环路定理,如式子9,。此外,U还与场强有联系:在平行金属板间,存在匀强电场,E=U/d(d表示物体初末位置沿电场线方向的距离),可见,E在定义式中有N/C、V/m两套单位。因此在平行金属板间W=qEd。

4.静电场学理论体系总结 综上所述,从电荷的性质到电荷受力,从电荷运动再到功能关系,我们就利用力、运动、功能的观点构建出经典关于静电场学的理论体系。进一步讲,在研究静电场学时先引出电场这一物质,再研究其性质进而得出它能使在电场中的物体受力,进而将电学与力学联系起来,再从受力推出运动,然后从运动推出物体对应的功能关系,如图1所示。

三、静电场学的实际应用举例
物理学的理论是解决实际问题的。在静电场学中常见的应用也有很多,以下是静电学应用的几个例子。
1.等势体,它是处于静电平衡状态的导体,由于导体内部电场不为零,自由电子就会做定向移动,导体两面的正负电荷就会增加,导体内部电场就会削弱,直到导体内部各点合电场为零为止,于是,导体内的自由电子不再定向移动,然后达到静电平衡状态(引用)。
2.电容器,在两个距离很近的平行金属板中间加上一层绝缘物质——电介质(引用)。充电后电容器两板之间形成电势差。电容是表示电容器容纳电荷本领的物理量,定义式为C=Q/U=ΔQ/ΔU,单位为法拉F。理论分析表明,C=εS/4πkd(当两极板充满一种介质时),为电容的决定式。关于它的动态分析,规律如下:当电容器与电源相连时U不变,当电容器与电源断开Q不变(当U不变时定义式与决定式联立再将 E=U/d代入得E=4πkQ/εS)。
3.静电计。它的金属杆和金箔与导体形成等势体,金箔的张角由它上面的电荷量决定。但对于静电计来说,金属箔常接地。当金属杆和金箔带电后,由于静电感应使金属瓶的内表面带上与金属瓶左右内壁组成了两个特殊的电容器,处于并联关系。当静电计带电后,相当于电容器充电,静电计内会形成电场且为匀强电场。金箔的张角越大,电势差越大。
四、经典静电场学理论体系存在的缺陷
尽管经典的静电场学的一些列重要理论成果为我们勾勒相对完善的理论体系,在实际工业技术生产中有着重要的应用,但对于电荷的受力运动问题,电流的形成的解释的还是初步的。十九世纪末至二十世纪初,汤姆生发现了电子、伦琴发现了X射线、原子内部粒子受力问题、测不准原理以及超导等诸多问题和现象致使近代的经典静电场学无法给予合理必要的解释。随着当代实验技术的进步以及计算物理的发展,针对电荷受力与运动问题研究提出了新的学说理论,诸如光电量子理论、耗散结构理论、自组织理论、混沌学说及其各种非平衡态的研究与探索为我们揭开相关问题的真理提供了新的方法。尽管这些新兴学说还是初步的或是存在不足,但人类始终会不断的探索下去。
参考文献:
[1]物理学.上册[M]/东南大学等七所院校遍,马文蔚,周雨青改编-6版,高等教育出版社 -2014.7,ISBN 978-7-04-039922-6
[2]物理学原理在工程技术中的应用[M].马文蔚主编-2版,高等教育出版社 -2011.11,ISBN 7-04-009807-5;
[3]Edward M.Purcell,Electricity and Magnetism[M],Berkeley Physics Coures-Volumbe2,Copyright2011 by McGraw-hill Education,ISBN 978-0-07-004908-6
