基于热流固耦合工作面前方瓦斯渗流数值模拟*

张　波，谢雄刚，刘洋成

(1.贵州大学 矿业学院，贵州 贵阳 550025；2.喀斯特地区优势矿产资源高效利用国家地方联合工程实验室，贵州 贵阳 550025；3.贵州省非金属矿产资源综合利用重点实验室，贵州 贵阳 550025)

0　引言

我国煤层地质条件复杂多变，煤层瓦斯含量大，据统计，全国有60%以上的煤矿属于高瓦斯或煤与突出矿井[1]。随着煤层开采深度的增加，温度、地应力和瓦斯含量增大，工作面前方瓦斯涌出量较多，容易导致煤与瓦斯突出事故[2]。且我国煤矿低渗透气性煤层较多，钻孔抽采瓦斯可以降低瓦斯含量，但较低的渗透率导致瓦斯抽采效果不佳，增加了煤矿开采的难度。因此，研究低渗透气性煤层在温度和地应力条件下瓦斯渗流规律显得尤为重要。

在研究煤层中瓦斯的运移规律时，学者们分析了煤与瓦斯的作用机理，认为煤体有效应力改变、瓦斯压力变化和温度升降会造成煤体变形，导致煤层孔隙率和渗透率发生改变，分别提出了各种数学模型来适应不同的地质条件。尹光志等[3-5]通过引入瓦斯吸附膨胀应力，建立了能描述含瓦斯煤流固耦合作用下的骨架可变形性和气体可压缩性的流固耦合模型，得出钻孔抽采瓦斯的有效半径会随着时间推移逐渐变大，最后趋于一个定值；鲜学福，周军平等[6-9]基于热力学方程建立了含瓦斯煤由吸附瓦斯引起的煤岩膨胀应变的理论模型，得到了吸附瓦斯引起的吸附膨胀变形；许江，李波波等[10]对不同温度条件下，型煤在瓦斯压力升降过程中瓦斯渗流特性进行了研究，得出在升降压作用下，瓦斯渗透率的变化规律；陶云奇[11]在流固耦合研究的基础上，提出了温度、地应力和瓦斯压力共同作用下的热流固三场耦合，并建立了相对应的数学模型，指出在深部开采时，温度不可忽略；范超军，李胜等[12]分析了地下水对瓦斯渗透率的影响，提出了瓦斯和水的相对渗透率来表征瓦斯-水两相流渗透率相互作用关系，建立了深部煤层瓦斯-水两相热-流-固耦合模型。然而，以上研究忽略了受采动影响下工作面前方温度、瓦斯压力和地应力的相互作用。本文通过模拟热流固耦合作用下瓦斯渗流过程，建立了工作面前方瓦斯运移规律数学模型。

1　深部瓦斯渗流模型

1.1　瓦斯运移模型

煤层内的瓦斯存在吸附和游离两种状态，吸附瓦斯占比80%～90%左右[13]，工作面前方受采动影响，在卸压区形成较多新鲜裂隙，大量吸附瓦斯转化为游离状态；由于在卸压区和应力集中区存在较大瓦斯压力梯度，煤层内部瓦斯渗流到工作面，充满整个工作面前方，造成工作面瓦斯涌出量剧增，在应力集中区容易发生瓦斯突出事故，如图1所示。

图1　工作面前方瓦斯运移模型Fig.1　Methane transport model in front of working face

1.2　基本假设

依据瓦斯赋存条件，提出以下假设：①煤是一种孔隙-裂隙双重介质的弹性体；②煤体被单项瓦斯所饱和；③游离瓦斯的惯性力、瓦斯的体积力忽略不计；④饱和孔隙-裂隙介质的体积变形包括骨架变形和孔隙、裂隙变形[14];⑤瓦斯在煤层中的渗流规律符合达西定律；⑥煤体中吸附游离瓦斯分别服从修正Langmuir方程和真实气体状态方程[15]；⑦煤体变形是微量的，处于线弹性变形阶段，服从广义虎克定律；⑧应力应变符号与弹性力学相同，压应力为负，拉应力为正，位移沿坐标轴正方向为正，反方向为负。

1.3　瓦斯运移模型控制方程

1.3.1应力场方程

煤体应变由3部分组成，包括瓦斯吸附膨胀(解吸收缩)引起的煤基质变形[16]，地应力对煤体的压迫变形，温度变化导致的热膨胀变形。三者共同作用相互耦合引起煤体发生变形，具体作用效果如图2所示。

图2　煤体受力变形Fig.2　Coal body force deformation

从宏观上看，煤颗粒排列疏松，在一定外应力作用下，一方面使煤颗粒排列更加紧密，另一方面压缩煤颗粒改变颗粒体积形状，使颗粒体积变小，进而导致孔隙率和渗透率变小；微观形态上，煤基质体积改变是由地应力压缩导致的地应力应变，瓦斯吸附膨胀(解吸收缩)引起的吸附膨胀(解吸收缩)应变，温度改变造成的热膨胀应变[17]。结合弹性力学中平衡微分方程和广义虎克定律，可以推出煤体受力变形的应力应变本构方程。

瓦斯压力引起的吸附膨胀应变：

(1)

式中：KY为体积压缩系数，MPa-1；p为瓦斯压力，Pa；p0为初始状态下瓦斯压力，Pa；ρ为煤的视密度，t/m3；R为普适气体常数，取8.3143；T为绝对温度，K；Vm=22.4×10-3m3/mol，为气体摩尔体积；a，b为煤的吸附常数。

热膨胀引起的应变：

(2)

地应力引起的应变：

(3)

式中：G为拉梅系数；υ为煤的泊松比；α为煤有效体积变形。

含瓦斯煤的总应变为:

ε=εp+εT+εW

(4)

THM耦合本构方程：

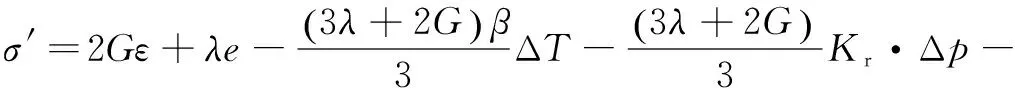
(5)

通过本构方程推出应力场方程的张量形式为：

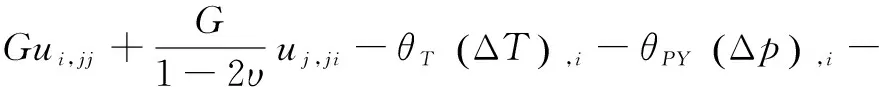
(6)

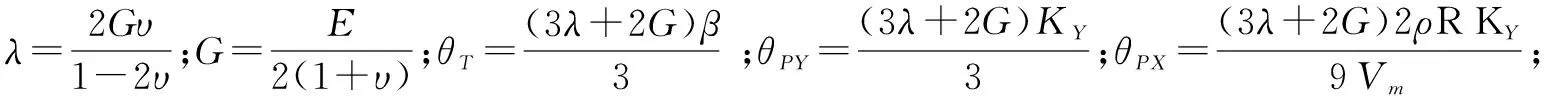
1.3.2渗流场方程

瓦斯在煤中的流动规律，在较大裂隙中符合菲克扩散定律，在小孔隙中遵循达西渗流定律，本文只研究煤层气在煤体中的渗流特性，因此，选用达西定律来计算渗透率，即：

(7)

(8)

(9)

式中：q为瓦斯渗流速度，m/s；▽p为瓦斯压力梯度，Pa/m;μ为气体运动粘度，Pa·s。

修正的langmuir方程和真实气体状态方程[18]为：

(10)

(11)

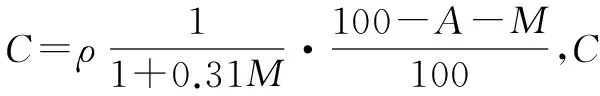
综合以上公式可以得出渗流场方程为：

(12)

式中：e为煤总体积形变；m为滑脱因子。

1.3.3温度场方程

在瓦斯流动过程中，煤层中瓦斯的吸附解吸和渗流都具有热效应，是一个非等温过程,含瓦斯煤在外力作用下发生的变形同样产生热效应[19]，因此渗流场、应力场和温度场存在着相互耦合作用。

温度场耦合方程为：

(13)

将方程(6)，(12)和(13)联立，即得到了深部煤层瓦斯渗流的THM模型，利用COMSOL Multiphysics的PDE方程模块、固体力学模块和热方程模块进行数值模拟。

2　工作面前方瓦斯渗流数值模拟

2.1　几何模型和边界条件

该模型选取贵州省盘州市松和煤矿15#煤层12150采煤工作面为工程实例，为了计算方便，沿回采面走向取单位厚度剖面作为计算的平面模型，模型长度和厚度分别为20 m和3 m。瓦斯渗流场边界条件：瓦斯在煤层中流动的初始瓦斯压力为p=1.27 MPa，工作面瓦斯压力为p0=0.1 MPa，煤层顶底板为岩层，瓦斯流量为0。应力场边界条件：在模型上下边界和左右边界位移为0，煤层受上覆岩层重力作用，上边界有均匀载荷，同时煤层自身重力作用一并考虑。温度场边界条件：煤层各边界设置温度为293 K，由于温度场的存在，煤层内部存在温度、瓦斯压力和地应力耦合作用，假设模型边界和外部不存在热量传递。计算过程中的基本参数如表1所示。

表1　数值模拟基本参数

2.2　工作面前方瓦斯压力变化规律

由于采动应力影响，工作面前方卸压区瓦斯裂隙较为发育，工作面煤壁瓦斯压力为0.1 MPa，与初始瓦斯压力1.27 MPa存在很大瓦斯压力梯度，应力的卸除，促进煤体内部瓦斯解吸释放，瓦斯从煤层内部运移到工作面，导致工作面瓦斯涌出量不断增加，煤层内部瓦斯压力逐渐降低。根据数值模拟得到不同时间点(5,10,15,20,25,30 h)的瓦斯压力分布特征(见图3～4)，工作面前方8 m内，从卸压区到应力集中区的过渡段，煤层瓦斯压力下降梯度较大，煤体解吸瓦斯沿裂隙快速释放，垂直应力的解除，释放很大能量，解释了该过渡段容易发生瓦斯突出的原因，也说明了应力集中区易发生煤与瓦斯突出。

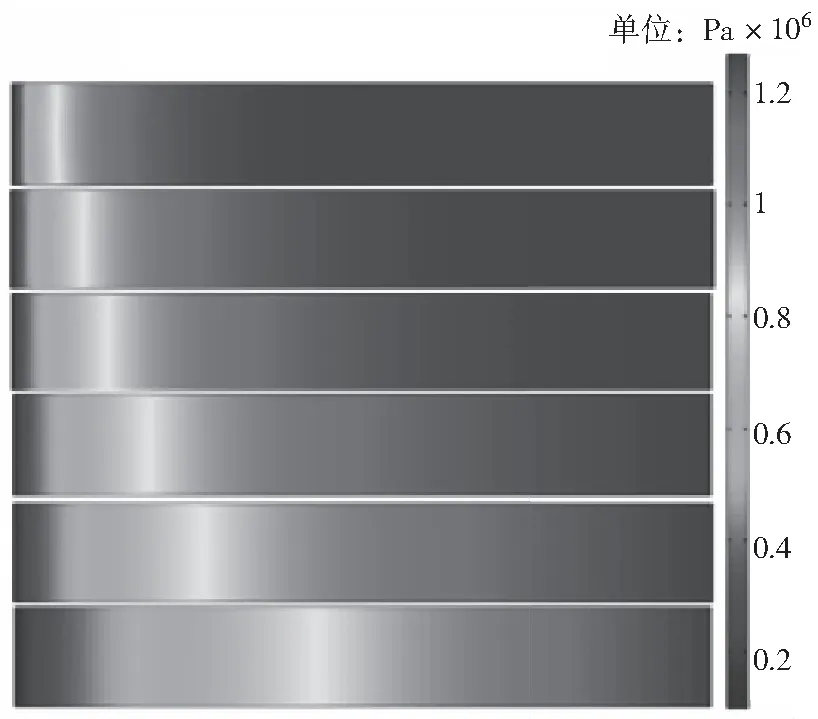
图3　各时间段瓦斯压力分布Fig.3　Distribution of gas pressure distribution in each time period

图4　工作面前方瓦斯压力变化Fig.4　Gas pressure changes in front of work surface

如图4可知，工作面前方20 m内，在0～10 m处瓦斯压力急剧升高，新鲜裂隙较多，瓦斯压力下降明显；从10～20 m 处瓦斯压力下降缓慢，位于应力集中区；20 m以后瓦斯压力为原始瓦斯压力。工作面前方5 m处，开采时间为5，10，15，20，25，30 h 的瓦斯压力分别为1.23，1.0，0.91，0.85，0.8，0.78 MPa。从应力集中区到卸压区，不同时间节点下瓦斯压力下降趋势随开采时间的增加，瓦斯压力梯度逐渐减小，吸附瓦斯含量降低，瓦斯总含量降低，瓦斯运移速率相对减慢；在工作面前方同一位置，瓦斯压力随着时间的增加逐渐降低，但降低速率减慢，最后，吸附瓦斯和游离瓦斯达到新的动态平衡，瓦斯压力趋于一个定值。图5为工作面前方1 m处不同时间节点的瓦斯压力分布，也符合以上分析规律。

图5　工作面前方1m处不同时间节点瓦斯压力分布Fig.5　Distribution of gas pressure at different time points at 1m ahead of working face

3　压力变化对渗透率的影响

孔隙率和渗透率由于有效压力、瓦斯压力和温度作用，从煤层内部到工作面，先降低后逐渐增大，最后趋于稳定。有效应力较高，压缩煤体，导致煤颗粒排列紧密，造成孔隙率相对较低，进而瓦斯渗透率较低，随着采煤活动的进行，内部裂隙逐渐增大孔隙率变大，瓦斯渗透率逐渐升高。

图6为渗透率随工作面长度变化规律。如图6所示，煤层深部未受采动影响的原始应力区，瓦斯渗透率为8×10-15m2，在应力集中区，瓦斯压力和有效应力较高，压缩煤体，导致煤颗粒排列紧密，渗流通道变窄，造成孔隙率相对较低，渗透率降低。在卸压区，煤体体积形变逐渐变大，产生了很多新裂隙，发生扩容，渗流通道贯通，导致渗透率急剧增加，因此在应力最大处形成了煤层渗透率最低点，并且随着时间的推移，渗透率最低点逐步远离工作面。工作面前方20 m处煤层渗透率趋于稳定为7.8×10-15m2，比初始渗透率偏低，这是由于深部煤层温度较高，使煤体颗粒变大，压缩孔隙和裂隙空间，导致煤层渗透率降低。

图6　渗透率随工作面长度变化规律Fig.6　Permeability with the change of working face length

4　温度变化对瓦斯渗流的影响

随着煤层深度加深，煤体温度有所上升，煤体温度升高时，一方面，瓦斯分子热运动加剧，吸附瓦斯获取一部分内能后，脱离煤基质表面成为游离瓦斯；另一方面，煤体受热后向内膨胀，使渗流通道变窄，减小渗流空间，导致渗透率减小。

图7为渗透率随温度变化规律。由图7可以看出随着温度从293～296 K变化中，渗透率从7.8×10-15降低到7.74×10-15，煤层渗透率逐渐减小，距离工作面越远处渗透率减小幅度越大。由此可知，在采煤工作面前方，煤层渗透率受温度影响，虽然温度升高后瓦斯热运动加剧，有促进瓦斯渗透率的趋势，但由于工作面前方外应力较大，煤体受热膨胀应力小于有效应力，导致煤体内膨胀，渗流空间减小，造成渗透率降低。综上可知，采煤工作面前方瓦斯渗透率受瓦斯压力梯度、煤层温度和有效应力相互影响，开采初期，瓦斯压力梯度较大，由于采动影响，产生大量裂隙和通道，瓦斯渗透率较大。随着开采进行，当温度升高时，煤体受热膨胀，但由于热膨胀应力小于有效应力，煤体内膨胀，渗流通道减小，渗透率降低。综合效果看，在同一位置，随着时间推移渗透率是逐渐减小的。

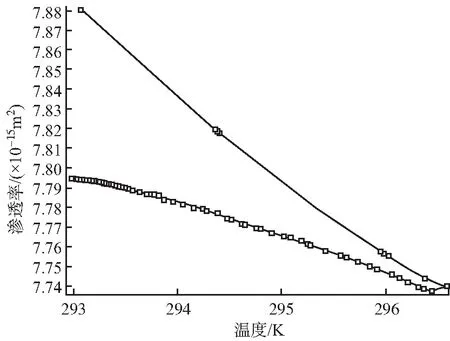
图7　渗透率随温度变化规律Fig.7　Permeability with temperature variation

5　结论

1)建立了工作面前方瓦斯渗流热流固耦合数学模型，通过数值模拟分析了煤层瓦斯压力和渗透率变化规律，给出了受工作面前方“三带”影响下，煤层瓦斯压力分布情况。从卸压区到应力集中区的过渡段，煤层瓦斯压力下降梯度较大，煤体解吸瓦斯沿裂隙快速释放，垂直应力的解除，释放很大能量，解释了该过渡段容易发生瓦斯突出的原因。

2)在采动影响下，在应力集中区，瓦斯压力和有效应力较高，压缩煤体，导致煤颗粒排列紧密，渗流通道变窄，造成孔隙率相对较低，渗透率降低。在卸压区，煤体体积形变逐渐变大，产生了很多新裂隙，发生扩容，渗流通道贯通，导致渗透率急剧增加，因此在应力最大处形成了煤层渗透率最低点为7.64×10-15m2。并且随着时间的推移，渗透率最低点逐步远离工作面。

3)在采煤工作面前方，虽然温度升高后瓦斯热运动加剧，有促进瓦斯渗透率的趋势，但由于工作面前方有效应力较大，煤体受热膨胀应力小于有效应力，导致煤体内膨胀，渗流空间减小，造成渗透率降低。

[1]张子敏.瓦斯地质学[M].徐州：中国矿业大学出版社，2009：2-3.

[2]陈亮.工作面前方煤体变形破坏和渗透率演化及其应用研究[D].北京：中国矿业大学，2016.

[3]尹光志，李铭辉，李生舟，等.基于含瓦斯煤岩固气耦合模型的钻孔抽采瓦斯三维数值模拟[J].煤炭学报，2013，38(4)：469-472.

YIN Guangzhi,LI Minghui,LI Shengzhou,et al.Three-dimensional numerical simulation of gas drainage by drilling based on gas-solid coupling model of coal and gas [J].Journal of China Coal Society,2013,38 (4):469-472.

[4]尹光志，李文璞，李铭辉，等.加卸载条件下原煤渗透率与有效应力的规律[J].煤炭学报，2014，39(8)：1497-1503.

YIN Guangzhi,LI Wenpu,LI Minghui,et al.Law of permeability and effective stress of raw coal under loading and unloading [J].Journal of China Coal Society,2014,39(8):1497-1503.

[5]尹光志，李文璞，李铭辉，等.不同加卸载条件下含瓦斯煤力学特性试验研究[J].岩石力学与工程学报，2013,32(5)：893-899.

YIN Guangzhi,LI Wenpu,LI Minghui,et al.Experimental study on mechanical properties of gas coal under different loading and unloading conditions [J].Chinese Journal of Rock Mechanics and Engineering,2013,32(5):893-899.

[6]周军平，鲜学福，李晓红，等.多孔介质中不混溶两相渗流的本构关系[J].四川大学学报(工程科学版)，2010，42(3)：107-111.

ZHOU Junping,XIAN Xuefu,LI Xiaohong,et al.Constitutive relationship of immiscible two-phase seepage in porous media [J].Journal of Sichuan University(Engineering Science Edition),2010,42 (3):107-111.

[7]董贺，王佰顺，李春亭.穿层预抽钻孔倾角与煤层气抽采效果关系的研究[J].中国安全生产科学技术，2015，11(2) :99-104.

DONG He,WANG Baishun,LI Chunting.Research on the relationship between pre-pumping borehole dip angle and coalbed methane drainage effect [J].Journal of Safety Science and Technology,2015,11(2):99-104.

[8]王臣，鲜学福，周军平，等.含不同气体煤岩全应力应变渗透特性试验研究[J].地下空间与工程学报，2013，9(3)：492-495.

WANG Chen,XIAN Xuefu,ZHOU Junping,et al.Experimental study of total stress and strain permeability of coal with different gas [J].Journal of Underground Space and Engineering,2013,9(3):492-495.

[9]周军平，鲜学福，姜永东，等.考虑基质收缩效应的煤层气应力场-渗流场耦合作用分析[J].岩土力学，2010，31(7)：2318-2322.

ZHOU Junping,XIAN Xuefu,JIANG Yongdong,et al.Coupling effect analysis of stress field-seepage field in coalbed methane considering matrix shrinkage effect [J].Rock and Soil Mechanics,2010,31(7):2318-2322.

[10]许江，张敏，李波波，等.不同温度条件下气体压力升降过程中瓦斯运移规律的试验研究[J].岩土力学，2016，37(6)：1580-1585.

XU Jiang,ZHANG Min,LI Bobo,et al.Experimental study on gas migration during gas pressure rise and fall under different temperature conditions [J].Rock and Soil Mechanics,2016,37 (6):1580-1585.

[11]陶云奇.含瓦斯煤THM耦合模型及煤与瓦斯突出模型研究[D].重庆：重庆大学，2009.

[12]范超军,李胜,罗明坤,等.基于流-固-热耦合的深部煤层气抽采数值模拟[J].煤炭学报,2016,41(12):3076-3085.

FAN Chaojun,LI Sheng,LUO Mingkun,et al.Deep CBM extraction numerical simulation based on hydraulic-mechanical-thermal coupledmodel[J].Journal of China Coal Society,2016,41(12) :3076-3085.

[13]肖伟晶，王晓军，李士超，等.渗透压力作用下岩石三轴压缩过程变形特性分析[J].中国安全生产科学技术，2017，13(12)：38-42.

XIAO Weijing,WANG Xiaojun,LI Shichao,et al.Analysis on deformation characteristics of rock in triaxial compression process with seepage pressure[J].Journal of Safety Science and Technology,2017,13(12):38-42.

[14]赵阳升.煤体-瓦斯耦合数学模型及数值解法[J].岩石力学与工程学报，1994，26(3)：229-239.

ZHAO Yangsheng.Coal-gas coupling mathematical model and numerical solution [J].Journal of Rock Mechanics and Engineering,1994,26 (3):229-239.

[15]李祥春，郭勇义，吴世跃.煤吸附膨胀变形与孔隙率、渗透率关系的分析[J].太原理工大学学报，2005，36(3)：264-266.

LI Xiangchun,GUO Yongyi,WU Shiyue.Analysis of the relationship between coal adsorption and expansion deformation,porosity and permeability [J].Journal of Taiyuan University of Technology,2005,36 (3):264-266.

[16]孙培德.SUN模型及其应用[M].北京：科学出版社，1995.

[17]马忠.基于热流固耦合的瓦斯抽采数值模拟研究[D].合肥：安徽理工大学，2014.

[18]题正义，潘进，田臣，等.7.0 m采高综采面回采巷道变形破坏规律研究[J].中国安全生产科学技术，2016，12(4)：57-61.

TI Zhengyi,PAN Jin,TIAN Chen,et al.Research on deformation and failure of mining gateway with height of 7 m in fully mechanized coal mining face [J].Journal of Safety Scienceand Technology,2016,12 (4):57-61.

[19]陈亮，吴兵，许小凯，等.泥、砂岩交互地层综放开采覆岩破坏高度的确定[J].采矿与安全工程学报，2017，4(3)：431-436.

CHEN Liang,WU Bing,XU Xiaokai,et al.Determine the failure height of overburden strata in fully mechanized caving mining with interaction between mud and sandstone [J].Mining and Safety Engineering Journal,2017,4(3):431-436.