气藏型储气库多周期注采储集层应力敏感效应
2021-11-03李继强赵冠群戚志林尹冰毅许寻方飞飞杨棽垚齐桂雪
李继强,赵冠群,戚志林,尹冰毅,许寻,方飞飞,杨棽垚,齐桂雪
(1.复杂油气田勘探开发重庆市重点实验室,重庆 401331;2.重庆科技学院石油与天然气工程学院,重庆 401331;3.中国石油化工股份有限公司中原油田分公司勘探开发研究院,河南濮阳 457000)
0 引言
建立储气库是解决天然气季节性消费不平衡,缓解供需矛盾的有效方法[1],气藏型储气库工作气量约占全球各类储气库总工作气量的 75%[2],是全球最主要的地下储气库类型。气井注采能力是储气库设计及评价的重要参数之一,胥洪成、谭羽非等研究了中国石油天然气集团有限公司多座在役储气库的运行动态,表明气井注采能力会影响储气库运行动态,制约储气库调峰能力[3-4]。此外,Zhou等多名学者研究了中国渤海等多个地区储气库地面设施参数配置,表明气井注采能力对储气库地面设施的运行参数、设备安全性和可靠性等均存在较大影响[5-7]。储气库高强度多周期注采导致储气库储集层岩石所受净应力发生周期性变化,储集层岩石物性在交变应力作用下受到严重损害,进而影响气井注采能力,制约储气库安全、长效运行[8]。因此,亟待厘清储气库储集层岩石渗透率应力敏感变化规律,明确储气库气井注采能力变化规律,为储气库储气层位优选、多周期运行动态准确预测提供技术支撑。
储集层岩石单周期应力敏感性研究较多,岩石覆压渗透率随净应力变化规律较明确[9-10],同时建立了储集层岩石覆压渗透率与净应力关系模型[11-12],并广泛应用于油气藏工程和数值模拟研究[13-14],但目前储集层岩石多周期应力敏感的相关研究相对较少。多位学者采用大港大张坨、中原文96等砂岩气藏型储气库岩样、人造砂岩岩样开展实验,认为在地下储气库多周期强注强采工作条件下,岩石渗透率不仅会随净应力上升而降低,还会随注采周期数增多而降低,且渗透率随注采周期数增多而降低的趋势随注采周期数增多而减缓[15-19]。目前,在覆压渗透率随净应力和注采周期的变化规律方面已经取得了初步成果,但仍存在两个问题亟待解决:①对导致岩石覆压渗透率随净应力和注采周期变化规律的内在机理尚未完全厘清;②目前已取得的成果认识均停留在定性阶段,尚未建立岩石覆压渗透率与岩石渗透率、净应力和净应力变化周期的关系模型,故在储气库气藏工程和数值模拟等研究中无法考虑储集层岩石多周期应力敏感问题。
本文选取中原油田文23储气库储集层标准岩样,开展不同物性岩样多周期注采条件下的渗透率应力敏感实验,测定不同净应力下岩样的覆压渗透率,分析岩样覆压渗透率随岩石净应力和注采周期的变化规律及内在机理,建立渗透率应力敏感指数与储集层岩石渗透率和储气库运行周期、初始覆压渗透率与岩石渗透率的关系模型,提出储气库多周期注采储集层覆压渗透率计算方法,研究多周期注采储集层应力敏感对储气库注采能力的影响程度。
1 多周期注采覆压渗透率变化规律
1.1 实验材料
根据文23储气库储集层岩石物性分布范围,筛选了 6块标准岩心作为实验岩样。岩心样品孔隙度10.24%~19.92%,渗透率(0.037 3~28.438 0)×10−3μm2(见表1),本文中渗透率指岩石绝对渗透率。实验用气为纯度99.99%的氮气。

表1 实验岩心基础数据表
1.2 实验设计
文 23储气库为气藏型储气库,上覆岩层压力为66.33 MPa,运行上限压力为38.62 MPa(与气藏原始地层压力一致),对应最小净应力为27.71 MPa,运行下限压力为19.06 MPa,对应最大净应力为47.27 MPa。根据储气库运行上限压力确定实验初始净应力为27.71 MPa,实验设计净应力测点间隔为2.5 MPa,实验最大净应力为47.27 MPa。实验温度为文23储气库地层温度120 ℃。
实验设计 7个净应力变化过程的覆压渗透率测试(见表2),采用定围压、变孔压的净应力变化方式,测定不同净应力下的覆压渗透率,实验装置如图 1所示。实验步骤为:①将岩样放入岩心夹持器中,设置围压66.33 MPa并保持恒定,注氮升压至38.62 MPa,按净应力测点间隔,从初始净应力开始,依次增大净应力至最大净应力,测定岩样的覆压渗透率;②按净应力测点间隔,从最大净应力开始,依次降低净应力至初始净应力,测定岩样的覆压渗透率;③更换岩样,重复步骤①—②至完成全部测试。
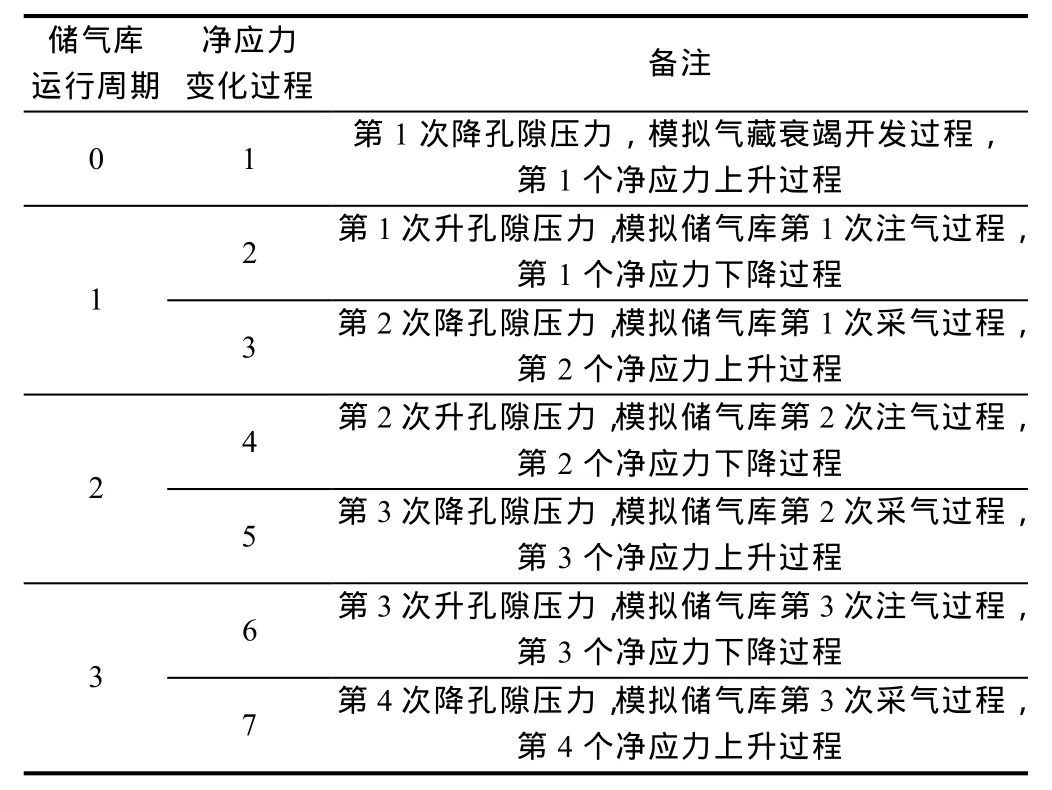
表2 储气库运行周期与净应力变化过程对照表

图1 多周期注采渗透率应力敏感实验装置图
1.3 结果分析
从覆压渗透率实验测试结果(见图2)来看,覆压渗透率随净应力的增大而降低。这主要是因为随着作用在岩样上的净应力的增大,岩样被压缩,岩样孔喉半径减小,故岩样覆压渗透率降低。由图2还可看出,各净应力变化过程中覆压渗透率与净应力关系曲线随净应力变化过程数的增多依次下移(覆压渗透率降低)。这是因为随着作用在岩样上的净应力的增大,岩样被压缩,岩样发生变形(弹性变形与塑性变形),覆压渗透率随净应力变化过程数的增多而降低,说明岩样在净应力上升被压缩时发生了一定的塑性变形。储集层岩石覆压渗透率随净应力上升而降低的现象即为岩石渗透率“应力敏感”,将储集层岩石覆压渗透率随净应力变化周期增多而降低的现象称为岩石渗透率“周期应力敏感”。

图2 不同净应力变化过程覆压渗透率与净应力关系曲线
目前,常用幂函数、指数函数、二项式或对数函数描述覆压渗透率与净应力的关系[20]。根据实验测试结果(见图2)分析,该区覆压渗透率与净应力呈较好的幂函数关系,可用幂函数描述单个净应力变化过程覆压渗透率与净应力的关系,即

将(1)式处理成无因次形式,则有

(2)式中,a为各净应力变化过程中无因次净应力(净应力与初始净应力的比值)等于 1时的无因次覆压渗透率,反映各净应力变化过程初始净应力下岩石覆压渗透率的保持率,第1个净应力变化过程初始净应力下的覆压渗透率(K)即为初始覆压渗透率(Ki),因而第1个净应力变化过程的a为1,1−a反映在净应力上升岩石被压缩时因塑性变形而闭合的那部分孔喉造成的岩石覆压渗透率降低的比率,通常称之为不可逆渗透率损失率;b反映了渗透率应力敏感性的强弱,b的数值越大,无因次覆压渗透率随无因次净应力上升而下降的速度越快,渗透率应力敏感性越强,反之则渗透率应力敏感性越弱。
根据实验测试结果,依据(2)式,对覆压渗透率和净应力进行无因次处理(见图 3),通过回归分析,确定每块岩样每个净应力变化过程的渗透率保持率和渗透率应力敏感指数(见表3)。

表3 渗透率保持率与渗透率应力敏感指数回归分析结果

图3 岩样3无因次覆压渗透率与无因次净应力关系曲线
图 4为不同岩样渗透率保持率与储气库运行周期关系曲线。可以看到,随着储气库运行周期数的增多,岩样因净应力上升被压缩发生塑性变形而闭合的喉道数量增多,相应地覆压渗透率下降幅度变大,渗透率保持率降低,渗透率保持率随储气库运行周期数增多而降低;随着储气库运行周期数的增多,岩样致密程度增加,岩样周期塑性形变量减小,闭合喉道数量减少,相应地岩样周期覆压渗透率下降幅度减小,渗透率保持率随储气库运行周期数增多而下降的速度减小。

图4 渗透率保持率与储气库运行周期关系曲线
由不同岩样渗透率应力敏感指数与净应力变化过程关系曲线(见图5)来看:①对于净应力上升过程,渗透率应力敏感指数随净应力变化过程数的增多而降低。因为过程数增多,岩样致密程度增大,岩样被压缩时能够闭合的喉道数量越来越少,故岩样渗透率降低幅度减小,渗透率应力敏感指数降低;②对于净应力下降过程,渗透率应力敏感指数随净应力变化过程数的增多基本不发生变化。因为净应力下降时,仅弹性变形可以恢复,各净应力上升过程的应力变化相同,故各净应力上升过程的弹性变形规律相同,净应力下降时弹性变形恢复规律也相同,因而渗透率应力敏感指数不随净应力变化过程数的增多而改变。

图5 渗透率应力敏感指数与净应力变化过程关系曲线
从图 5还可看出,随净应力变化过程数的增多,特定岩样净应力上升过程与净应力下降过程的渗透率应力敏感指数不断趋近。净应力上升过程中,随净应力上升,岩石发生弹性变形和塑性变形;净应力下降过程中,随净应力下降,仅弹性变形可以恢复。对于特定岩样,净应力上升时的弹性形变量和塑性形变量之和大于净应力下降时弹性形变量,则净应力上升过程的渗透率应力敏感指数大于净应力下降过程的渗透率应力敏感指数,当净应力上升时的塑性形变量随净应力变化过程数的增多而趋于 0时,净应力上升时岩样的形变量等于净应力下降时岩样的形变量,此时净应力上升过程的渗透率应力敏感指数等于净应力下降过程的渗透率应力敏感指数。
从储气库同一运行周期不同岩样不可逆渗透率损失率与渗透率关系曲线(见图6)来看,岩样渗透率越低,不可逆渗透率损失率越大,岩样周期应力敏感性越强。这主要是由于岩样渗透率越低,岩样净应力上升被压缩时因塑性变形而闭合的喉道数量越多所致。
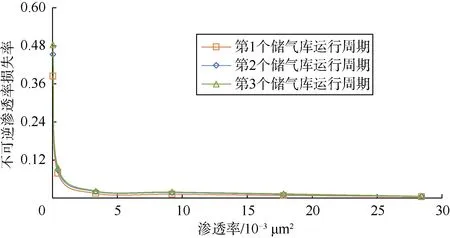
图6 不可逆渗透率损失率与渗透率关系曲线
由同一净应力变化过程不同岩样的渗透率应力敏感指数与渗透率关系曲线(见图7)可以看到,岩样渗透率越低,渗透率应力敏感指数越大,岩样应力敏感性越强。这主要是由于岩样渗透率越低,岩样孔喉半径越小,在净应力上升岩样被压缩时喉道闭合的数量越多,岩样渗透率降低幅度越大所致。

图7 渗透率应力敏感指数与渗透率关系曲线
2 多周期注采覆压渗透率计算方法
根据前述分析,可用(2)式描述岩样单个净应力变化过程覆压渗透率与净应力的关系,且(2)式中的渗透率保持率和渗透率应力敏感指数均与岩石渗透率和储气库运行周期相关。
2.1 计算渗透率应力敏感指数
对表 3中的渗透率应力敏感指数与岩样渗透率数据作图并进行回归分析(见图 8),发现同一净应力变化过程的渗透率应力敏感指数与岩样渗透率之间呈较好的幂函数关系(相关回归参数见表 4),可采用统一的函数关系表示如下:


图8 渗透率应力敏感指数与渗透率关系

表4 e和f回归分析结果统计表
对于净应力下降过程,由于特定岩样渗透率应力敏感指数随净应力变化过程数的增多基本不发生变化(见图9),因而 e和 f基本保持不变,与净应力变化过程的关系曲线基本为水平线。将各净应力下降过程的e和f进行平均处理,而后代入(3)式,可得该储气库净应力下降过程中的渗透率应力敏感指数计算模型为:

图9 e、f与净应力变化过程关系曲线

净应力上升过程中,随净应力变化过程数的增多,特定岩样渗透率应力敏感指数降低并趋近于净应力下降过程中的渗透率应力敏感指数,且岩样渗透率越低,这种降低并趋近的速度越快(见图8),故随净应力变化过程数的增多,净应力上升过程的e和f分别趋近于净应力下降过程的e和f(见图9)。
净应力上升过程与净应力下降过程的Δe和Δf与净应力变化过程数呈很好的幂函数关系,采用幂函数回归分析,可建立Δe和Δf与净应力上升过程关系模型(见图10)。净应力下降过程的e和f为定值,分别为0.063 83和0.344 7,则净应力上升过程中的e和f与储气库运行周期的关系模型为:
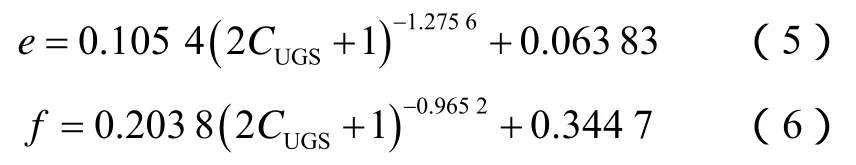
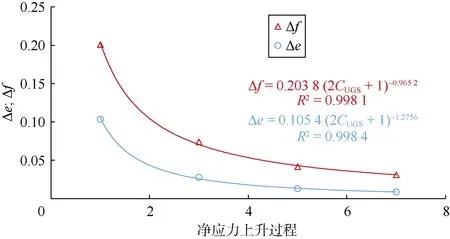
图10 Δe和Δf与净应力上升过程关系
将(5)式和(6)式代入(3)式,可得净应力上升过程渗透率应力敏感指数计算模型为:
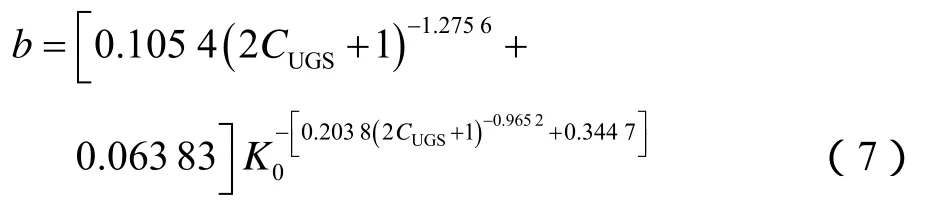
给定岩石渗透率,采用(4)式可计算净应力下降过程中的渗透率应力敏感指数,采用(7)式可计算任意储气库运行周期净应力上升过程的渗透率应力敏感指数。
2.2 计算渗透率保持率
不同净应力变化过程的无因次覆压渗透率与无因次净应力关系曲线是连续的,每一个净应力变化过程终点对应的无因次净应力和无因次覆压渗透率也即下一个净应力变化过程起点对应的无因次净应力和无因次覆压渗透率(见图3)。第1个净应力变化过程的渗透率保持率恒为1,根据无因次覆压渗透率与无因次净应力关系曲线的连续性,给定储集层岩石渗透率,综合(2)、(4)和(7)式可递推计算出任意净应力变化过程的渗透率保持率。
2.3 计算覆压渗透率
给定岩石渗透率和储气库运行周期,可计算确定渗透率应力敏感指数和渗透率保持率,而后采用(2)式可计算给定无因次净应力下的无因次覆压渗透率。实验室测得的岩心样品渗透率和测井解释得到的储集层渗透率通常都是岩石在较小的净应力下的渗透率。因此,在得到给定无因次净应力下的无因次覆压渗透率之后,要计算岩石的覆压渗透率,需要建立岩石初始覆压渗透率(第 1个净应力变化过程初始净应力下的覆压渗透率)与岩石渗透率(岩石在较小的净应力下的渗透率)之间的转换关系式。
根据6块岩心样品测试结果分析(见图11),该储气库初始覆压渗透率与渗透率之间呈如下关系:
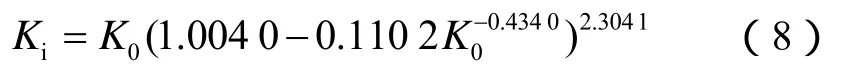
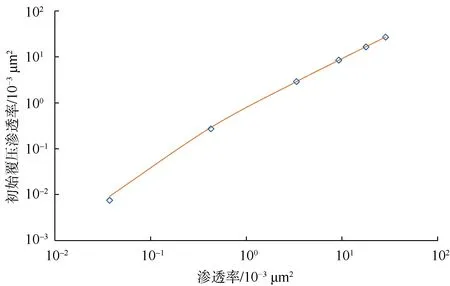
图11 初始覆压渗透率与渗透率关系
则覆压渗透率为
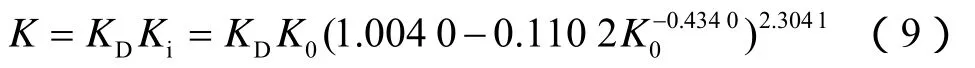
通过计算得到无因次覆压渗透率后,采用(9)式可计算覆压渗透率。给定储集层岩石渗透率,综合(2)、(4)、(7)和(9)式,采用前述方法可计算任意储气库运行周期、任意净应力下岩石覆压渗透率。
3 应力敏感对气井注采能力的影响
文 23 储气库储集层平均渗透率 1.00 1×10−3μm2,储集层平均厚度 69 m,平均井距 300 m,井筒半径0.078 55 m。根据储集层平均渗透率,采用本文提出的多周期注采覆压渗透率计算方法,可得到不同储气库运行周期、不同净应力下的覆压渗透率,进而采用气体平面径向拟稳定流动产量计算公式[21],得到气井的无阻流量:

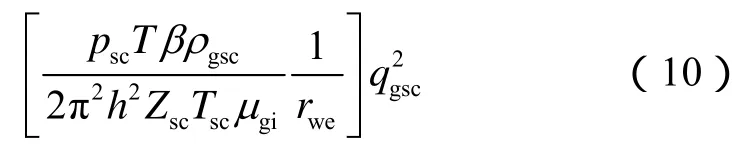
从覆压渗透率、气井无阻流量与储气库运行周期关系曲线(见图12、图13)来看,随储气库运行周期数的增多,覆压渗透率初期快速下降,后期缓慢下降;气井无阻流量(气井生产能力或注入能力)同样呈现出初期快速下降,后期缓慢下降的变化规律。
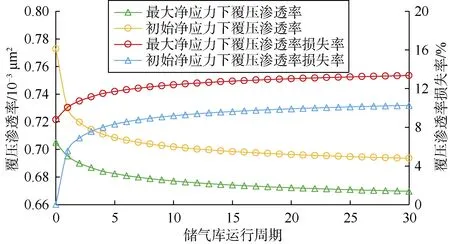
图12 覆压渗透率及损失率随储气库运行周期变化曲线

图13 气井无阻流量及损失率随储气库运行周期变化曲线
储集层初始覆压渗透率为 0.772 9×10−3μm2,第 30个储气库运行周期初始净应力下的覆压渗透率为0.693 5×10−3μm2,不可逆渗透率损失率为 10.27%。气井初始无阻流量为62.19×104m3/d,第30个储气库运行周期初始净应力下气井无阻流量为57.41×104m3/d,损失率为7.68%。
第30个储气库运行周期最大净应力下的覆压渗透率为 0.669 7×10−3μm2,相比初始覆压渗透率降低了0.103 2×10−3μm2,损失率为 13.35%。第 30 个储气库运行周期最大净应力下气井无阻流量为 55.94×104m3/d,比初始无阻流量下降了 6.25×104m3/d,损失率为10.05%。
气井生产、注入能力在前 5个储气库运行周期下降幅度最大,而后下降幅度减缓。气井在前 5个运行周期初始净应力、最大净应力下的无阻流量损失率分别为6.21%和8.78%,分别占30个运行周期气井无阻流量总损失的80.86%和87.36%。
4 应力敏感对储气库选层的指导作用
多周期注采覆压渗透率变化规律研究结果表明,岩石渗透率越低,其应力敏感性和周期应力敏感性越强(见图 6、图 7),气井注入能力和产出能力下降幅度越大,因而渗透率过低的储集层不宜作为储气库选层。
文 23储气库储集层渗透率在 0.01×10−3~100.00×10−3μm2,采用本文提出的多周期注采覆压渗透率计算方法,计算总渗透率损失率,结果表明储集层渗透率低于0.30×10−3μm2时,总渗透率损失率随渗透率降低而急剧增大,由此可确定文23储气库选层渗透率下限为0.30×10−3μm2。渗透率低于该下限值的储集层具有较强的周期应力敏感性和应力敏感性,不能满足储气库强注强采需求。
5 结论
岩石渗透率保持率随储气库运行周期数增多初期快速降低,后期缓慢降低;净应力上升过程中渗透率应力敏感指数随净应力变化过程数的增多而降低;净应力下降过程中渗透率应力敏感指数基本不随净应力变化过程数的变化而变化;随净应力变化过程数的增多,特定岩石净应力上升过程的渗透率应力敏感指数不断趋近于净应力下降过程的渗透率应力敏感指数。
岩石渗透率越低,不可逆渗透率损失率越大,岩石周期应力敏感性越强;岩石渗透率越低,渗透率应力敏感指数越大,岩石应力敏感性越强,渗透率过低的储集层不宜作为储气库选层。
储集层渗透率应力敏感性对气井注采能力影响较大,且主要集中在前数个周期。
符号注释:
a——渗透率保持率;b——渗透率应力敏感指数;CUGS——储气库运行周期数;e——应力敏感指数方程系数;f——应力敏感指数方程指数;h——地层有效厚度,m;K——覆压渗透率,10−3μm2;K0——岩样渗透率,10−3μm2;KD——无因次覆压渗透率;Ki——初始覆压渗透率(第 1个净应力变化过程初始净应力下的覆压渗透率),10−3μm2;Kg——气相有效渗透率,10−3μm2;m——覆压渗透率与净应力关系方程系数;n——覆压渗透率与净应力关系方程指数;peob——净应力,MPa;peobi——初始净应力,MPa;psc——标准状况压力,MPa;qgsc——标准状况下气井产气量,m3/ks;re——气井泄流半径,m;rwe——井筒折算半径,m;T——地层温度,K;Tsc——标准状况温度,K;Zsc——标准状况下气体压缩因子;β——非达西渗流系数,pm−1;Δe——净应力上升过程与净应力下降过程应力敏感指数方程系数之差;Δf——净应力上升过程与净应力下降过程应力敏感指数方程指数之差;μgi——初始地层条件下气体黏度,mPa·s;ρgsc——标准状况下气体密度,kg/m3;ψwf——井底流压下气体拟压力,MPa2/(mPa·s);ψR——平均地层压力下气体拟压力,MPa2/(mPa·s)。
