电渣重熔过程流场和温度场的数值模拟
2018-04-11韩丽辉于春梅曲明磊
韩丽辉, 于春梅, 曲明磊
(北京科技大学 冶金与生态工程学院,北京 100083)
0 引 言
电渣重熔(Electro Slag Remelting,ESR)是利用电加热渣来重熔自耗电极进行精炼铸锭的一种方法,它能够有效消除偏析、缩孔、疏松等缺陷。由于存在熔滴和熔渣的冶金反应,经电渣重熔的钢具有纯度高、含硫低、非金属杂质少、钢锭表面光洁、组织均匀致密、金相组织和化学成分均匀等优点,因此电渣重熔技术越来越多地应用到高温合金、精密合金、模具钢、航天军用钢等特殊钢以及铝、铜、银等有色金属合金生产领域[1,2]。在电渣重熔生产过程中,熔池形状和深度影响着结晶的方向[3];渣池温度场及流场与自耗电极末端形状、尺寸及熔化速度之间相互影响;供电方式、电流大小、填充比及电极浸入深度同样影响渣池的温度分布、金属熔池的形成和渣皮的厚度等重要的工艺指标[4],因此分析电渣重熔过程中的温度场和流场对于控制相应的工艺参数提高重熔铸锭质量有重要的意义。由于ESR过程处于高温大电流环境,通过实验测量手段对其流场温度场进行研究存在一定困难,因此近年来国内外许多学者通过数值模拟方法在ESR研究方面做了很多工作[5-10]。
从数值模拟方法上看,景馨等使用有限元软件ANSYS计算电磁场和温度场[11-14];文献[15-17]中利用ANSYS软件计算出焦耳热和洛伦兹力,将二者导入流体计算软件FLUENT中,分别作为能量方程和动量方程的源项来计算温度场和流场,没有考虑流体运动对磁场的影响;文献[18-19]中利用Meltflow、CAE软件计算电磁场和温度场;文献[5,7,20-22]中采用有限差分方法模拟具体条件下电渣重熔过程的计算程序;文献[7,23]中求解外加磁场二维传输方程,也没有考虑流动对磁场的影响;电渣重熔体系内流体的流动属于磁流体流动范畴,本文采用流体计算软件FLUENT中的磁流体模块(Magneto hydro dynamics,MHD),求解由于流动引起的附加磁场传输方程,因交变电流产生的外部磁场由有限元计算软件ANSYS求解,然后通过C语言编写的转换程序将外部磁场数据导入到FLUENT中,由外部磁场和附加磁场共同产生的焦耳热和电磁力作为源项加入到能量方程和动量方程中,最终由FLUENT耦合求解流场及温度场。
1 电渣重熔过程
电渣重熔的基本原理如图1所示。在铜制水冷结晶器内盛有熔融的炉渣,自耗电极一端插入熔渣内。自耗电极、渣池、金属熔池、钢锭、底水箱通过短网导线和变压器形成回路。在通电过程中,渣池放出焦耳热,将自耗电极端头逐渐熔化,熔融金属汇聚成液滴,穿过渣池,落入结晶器,形成金属熔池,受水冷作用,迅速凝固形成钢锭。在电极端头液滴形成阶段,以及液滴穿过渣池滴落阶段,钢-渣充分接触,钢中非金属夹杂物及有害元素为炉渣所吸收,从而达到净化金属熔液的目的,同时渣池可以隔绝空气起到精炼作用。上升的熔池在钢锭外层形成一层薄渣壳,不仅使钢锭表面光洁,还起到绝缘和隔热作用,使更多的热量向下部传导,有利于钢锭自下而上的定向结晶[23-24],等到结晶器内的液相完全凝固后,可以进行脱锭,完成整个生产过程。

图1 电渣重熔工作原理图
2 数学模型
数值模拟就是数值求解描述物理问题的微分或积分方程组,而数学模型就是描述物理问题的控制方程及边界条件。描述电渣重熔过程所用基本控制方程包括麦克斯韦方程组、质量守恒方程(连续方程)、动量守恒方程和能量守恒方程。电渣重熔与普通流动传热问题最大的不同在于导电流体内部产生电磁场,流体受到电磁力并产生焦耳热,流动的驱动力就是电磁力以及焦耳热差异导致的浮升力,所以电磁力和浮升力以源项形式加到动量方程中,焦耳热也以源项形式加到能量方程中。为了简化计算过程,假设:① 忽略电极运动,电极端头采用平头形状;② 侧面的渣壳起到电绝缘作用;③ 渣和钢液的密度、渣的电导率随温度变化,其他属性均为常数[17];④ 不考虑磁扩散的影响;⑤ 不考虑钢锭周围空气隙引起的接触热阻;⑥ 重熔过程温度超过居里点,钢锭及钢液均从铁磁体变为顺磁体,相对磁导率为1。
2.1 电磁场控制方程
麦克斯韦方程组由如下4个方程组成[25]:
(1)
(2)
(3)
(4)
电流连续方程(电荷守恒):

(5)
电磁场本构关系:
(6)
D=εE
(7)
欧姆定律:
J=σE
(8)
式中:H为磁场强度,A/m;B为磁感应强度,T;E为电场强度,V/m;D为电位移,C/m2;J为电流密度,A/m2;μ为磁导率,H/m;ε为电容率,F/m;σ为电导率,1/(Ω·m);q为体电荷密度,C/m3;t为时间,s。
电渣重熔使用交流电,交变电流产生的磁场和电场相互影响,可用麦克斯韦方程组描述,由于渣、金属熔池和铸锭充分导电且为低频状态,可忽略体电荷密度和位移电流[25],式(3)忽略,式(1)变为:

(9)
式(5)变为:

(10)
考虑到带电流体在磁场中的速度效应,式(8)变为:
J=σ(E+U×B)
(11)
式中:U为流体速度矢量,m/s。
由麦克斯韦方程组、电流连续方程及欧姆定律得到导电流体电磁场的磁感应强度传输方程:

(12)
求解出磁感应强度后,根据式(9)(6)求得电流密度。
如何求解磁感应强度传输方程是解决电磁场问题的关键,考虑到磁场由外加磁场和流体运动产生的感应磁场共同作用而成,得到:
B=B0+b
(13)
式中:B0为外加感应磁场,与流体运动无关;b为由于带电流体运动而产生的感应磁场,也就是磁流体的速度效应。
B0的传输方程为:
(14)
b的传输方程为:


(15)
外加感应磁场B0由有限元计算软件ANSYS通过矢量磁位法求解,磁场和电场与矢量磁位的关系[26]:

(16)
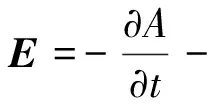
(17)
式中:A为矢量磁位,(Vs)/m;φ为标量电位,V。
利用SOLID97单元求得矢量磁位和标量电位,再由式(16)得到磁感应强度B0。将B0的实部和虚部按照FLUENT MHD模型要求的格式导入到流体计算软件FLUENT中,由FLUENT求解b的传输方程。在FLUENT中通过编写UDF,求解电流密度,电磁力(洛伦兹力)及焦耳热:
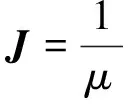
(18)
Fe=J×B
(19)
(20)
式中:Fe为电磁力,N/m3;Q为焦耳热,W/m3。
2.2 流场控制方程
描述流体运动的连续方程和动量守恒方程在电渣重熔问题中同样适用,只是流动主要由电磁力和浮升力引起的,属于湍流流动,但湍流强度不大;假设粘度为常数,密度使用Boussinesq假设,该假设只是用于计算浮升力Fb,方程中其他项中的密度为常数。另外由于钢液发生凝固,在固液两相区流动受到阻力,作为多孔介质区域处理(也称焓-多孔介质法),所以在动量方程及湍流方程中要加上相应的源项。
连续方程:

(21)
动量方程:


(22)
Fb=-ρ0β(T-T0)g
(23)
(24)
式中:ρ0为T0时的密度,kg/m3;T0、T分别为参考温度和流体温度,K;β为热膨胀系数;μeff为有效黏性系数,kg/(m·s);p为压强,N/m2;q为体电荷密度,c/m3,对于高电导率的低频条件,体电荷密度可忽略不计;Fe为电磁力,N/m3;g为重力加速度,m/s2;Sp为由于凝固引起的流动阻力,N/m3;fl为固液两相区液相比例,Amush为两相区常数,为了使液固界面清晰设为107[15];Up为铸锭拉速,m/s,实为渣层上升速度,该选项利于连续方程收敛,但由于数量级很小可以忽略[27]。
湍流模型主要用来计算有效粘性系数,选择RNGk-ε湍流模型及提高型近壁面函数,该模型适用于低雷诺数的湍流流动。计算域中包括渣和钢液属于多相流,选择VOF模型,该模型适合于两相间有明显的分界面,针对第二相求解体积比传输方程,两相的体积比之和为1,设钢液为第二相。表面张力影响着液滴的形成和钢渣界面形状,采用连续性表面张力模型。
2.3 能量方程
通过求解能量方程得到温度场。由于发生相变,焓中要考虑凝固释放的潜热,固液模糊区的焓值通过液相比例设定。焦耳热作为源项加到能量方程中,
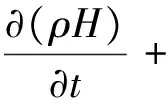
(25)
H=h+flL
(26)
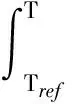
(26)
fl=(T-TS)/(TL-TS)
(27)
式中:keff为有效导热系数,W/(m·K),href为参考温度下的参考焓值,J/kg;L为钢液凝固释放出来的潜热,J/kg;Cp为钢液比热,J/(kg·K);TS钢液固相线温度,K;TL钢液液相线温度,K。
2.4 边界条件
ANSYS求解外加电磁场,利用矢量磁位法将xyz3个方向上的磁位和电位作为未知量,电极、渣、钢以及外围空间为计算域。电极一端为电流边界条件,耦合该面上电压,钢锭底部电压约束为0,周围空间外表面为磁力线平行边界条件。
用FLUENT进行多物理场耦合计算,计算域不包含电极部分,只包含渣池和金属域。以电极与渣池接触面为液态金属速度入口边界,温度高出液相线温度20 K。虽然金属熔池的焦耳热是周期性变化的,但因其周期很短(为0.02 s),可以认为金属熔滴是匀速滴落的;取钢锭下表面为流量出口边界;渣池与空气接触面采用剪应力为零边界条件,换热方式为对流和辐射混合模式;其他面为墙壁,采用无滑移壁面边界条件,换热采用对流换热。在FLUENT中通过自定义标量(UDS)求解由于流体运动产生的感应磁场,壁面为绝缘壁。边界条件参数见表1。

表1 边界条件具体参数
3 模型调试
3.1 几何模型及网格划分
ANSYS计算域包括电极、渣池、金属铸锭及其周围空间,如图2、3所示。取空间半径约为渣池半径的10倍左右,电极高度对计算结果影响不大。电极、渣池及金属铸锭为核心计算域,为了减少计算量,核心域网格尺寸比外围空间小得多。核心域采用SWEEP方式划分六面体(HEX)网格,网格尺寸10 mm;外围空间采用四面体网格,网格尺寸0.1 m。FLUENT计算域只包括渣池和铸锭,全部为六面体网格。几何模型尺寸:电极直径为55 mm;铸锭直径为0.12 m;外围空间直径为1.2 m;渣池高度为60 mm;铸锭高度为0.215 m;电极浸入深度为2 mm;电极高度为0.1 m。

图2 ANSYS计算域几何模型图3 FLUEN计算域几何模型
3.2 MHD模型及外加磁场导入转换
FLUENT中的MHD模型包括两种求解电磁场方法,一是磁感应法,求解由于流体运动引起的感应磁场;二是电位法,忽略流体运动引起的感应磁场,且外加磁场是由直流电场产生的静态磁场。电渣重熔使用交流电,且考虑磁流体的速度效应,属于流动导体介质内的磁感应问题。通过定义自定义标量uds-0(bx)、uds-1(by)、uds-2(bz),求解其传输方程,再通过自定义函数UDF求解电场强度、电磁力以及焦耳热等并存储在自定义内存(UDM)中。FLUENT耦合求解多个控制方程,其求解机理见文献[28]。
外加磁场由ANSYS计算得到,MHD模型需要的实部虚部数据,所需数据域为一个立方体,该立方体的大小要把FLUENT计算域包含在内。立方体需要划分多个网格,其网格尺寸与ANSYS网格尺寸差不多。立方体大小的定义、网格划分以及得到每个网格节点的磁场数据都由C语言编写的数据转换程序完成。图4中C为立方体中任意网格,其磁场数据可由加权法或插值法得到,两种方法得到的磁场数据基本相同,见图5、6。
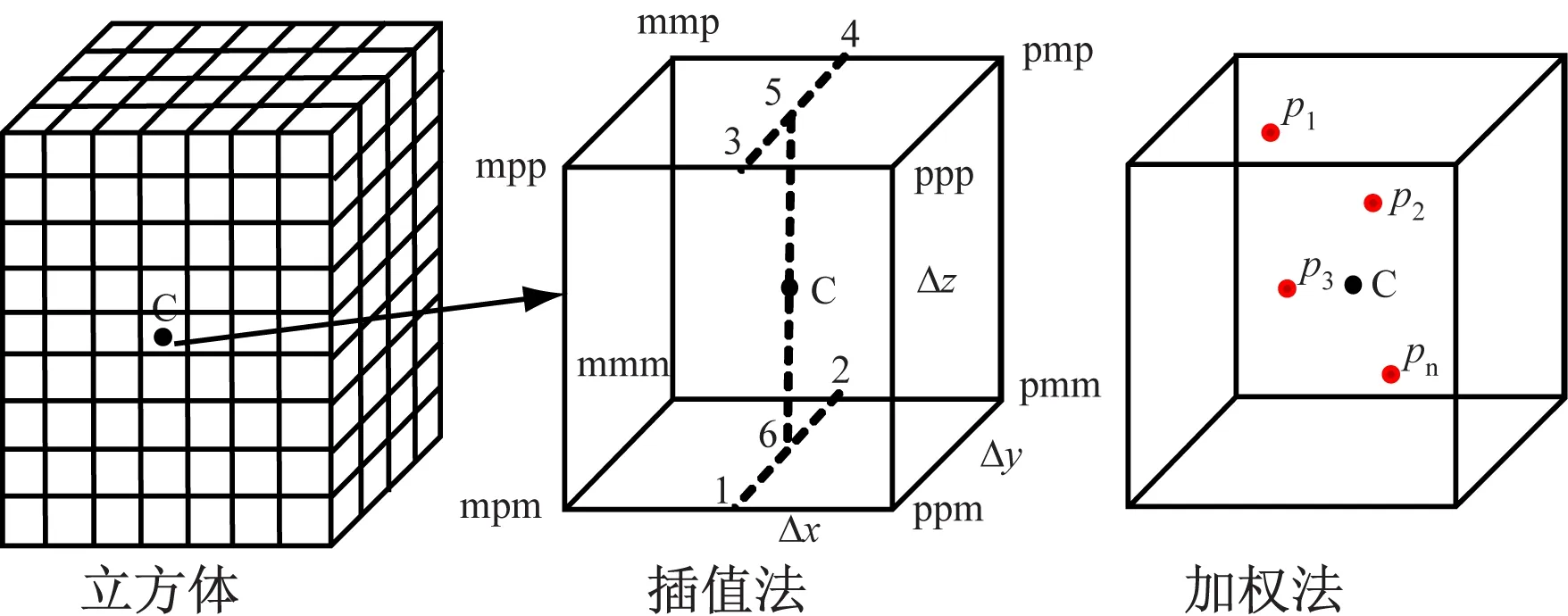
图4 数据转换示意图
加权法认为一个网格内包含有多个ANSYS节点数据,网格中心磁场由这些点叠加得到,且离中心越远的贡献的磁场越小,权重与距离倒数成正比:
(28)
(29)
式中:BC为网格中心磁场数据;Bi为Pi点磁场数据,由ANSYS计算得到;vi为Pi点权重,Li为Pi点到网格中心的距离,m。

图5 加权法得到的磁场数据图6 插值法得到的磁场数据
插值法即定义好网格C的中心点坐标后,找到其周围8个方向上离中心最近的8个点进行插值。如点pmp的顺序为xyz,p表示增加方向(plus),m表示减小(minus),pmp表示x方向增加、y方向减小、z方向增加。找到8个点后进行插值,插值顺序从边长小的方向开始,如△x<△y<△z,插值则先从x方向插值,得到1、2、3、4个点的值;再进行y方向插值,由1、2得到5点值,由3、4得到6点值;最后z方向插值,由5、6得到网格中心的值。1点的插值式为:
(30)
其他点雷同。
式中Bmpm及Bppm为mpm点和ppm点的磁场数据,由ANSYS计算得到。
3.3 关键参数
渣池内热浮升力的计算采用Boussinesq模型,需要设置参考温度以及该温度下熔渣的参考密度,参考温度设置的是否合理将影响流场分布[29]。时间步长影响液滴形成及低落过程,一般采用较小的时间步长,如0.001。金属的导热系数影响温度场的分布,最终会影响金属熔池的形貌,文中采用piecewise-polynomial方法将固、液两相区域分开设置。渣池焦耳热与电渣的电导率有关,电导率随温度变化而变化,最终会影响温度场的分布。具体物性参数见表2。
3.4 初始化
合理的初场设置有利于控制方程的收敛并缩短计算时间,采用hybrid方式初始化有利于得到合理的速度初场。因外加磁场产生的焦耳热是周期性变化的,没有必要进行温度初场的计算,直接采用较小时间步长(步长可为周期的1/20)同时计算所有方程。
4 结果分析
4.1 MHD模型
MHD模型的计算结果中包括外加磁场、由于运动产生的磁场、电流密度、电场及洛伦兹力及焦耳热,见图7~12。从结果中可以看出电流密度和外加磁场方向符合右手螺旋定则,洛伦兹力与电流方向及磁场方向之间符合右手定则;电场强度方向与电流方向一致,由于金属的电导率要比电渣的电导率大得多,所以金属域的电场强度要远远小于渣池的电场强度;由于某点磁场是电荷在该点产生的磁场叠加合成,从图7中可以看出沿半径方向磁感应强度增加且呈线性变化,由于集肤效应进入到熔池的电流密度在径向分量可以忽略,另外由于涡流效应渣池部分的磁感应强度大于钢锭部分的磁感应强度[12];从图8可以看出,由于流体在磁场中的运动而产生的附加磁场同外加磁场相比很小很小,完全可以忽略不计,其磁雷诺数为4.16×10-5,符合文献[7]中当磁雷诺数远远小于1时不考虑运动附加磁场的结论;从图9可以看出,电流进入到熔池后,流经渣池、金属熔池、钢锭后返回到变压器,在渣域由于金属熔滴电阻远小于渣池电阻,所以熔滴电流密度较大;从图11可以看出,洛伦兹力方向指向对称轴,且在电极底部周围附近最大,越靠近对称轴越小,有利于渣池形成中间向下四周向上的漩涡流动;从图12可以看出,在渣池内电极下方位置的焦耳热最大,从而有利于自耗电极的熔化滴落,另外金属域的焦耳热要比电渣域的小的多,这是因为金属的电阻远远小于电渣的电阻;文中MHD模型计算结果与文献[23]基本一致。

表2 物性参数表

图7 外加磁场矢量图图8 流动附加磁场矢量图

图9 电流密度矢量图图10 电场强度矢量图

图11 洛伦兹力矢量图图12 焦耳热云图
4.2 流场及熔滴
渣池内的流动主要由洛伦兹力和浮升力引起,图13为渣池流动的速度场。从图中可以看出,由洛伦兹力引起的渣的流动呈漩涡状,中间部分向下四周向上,
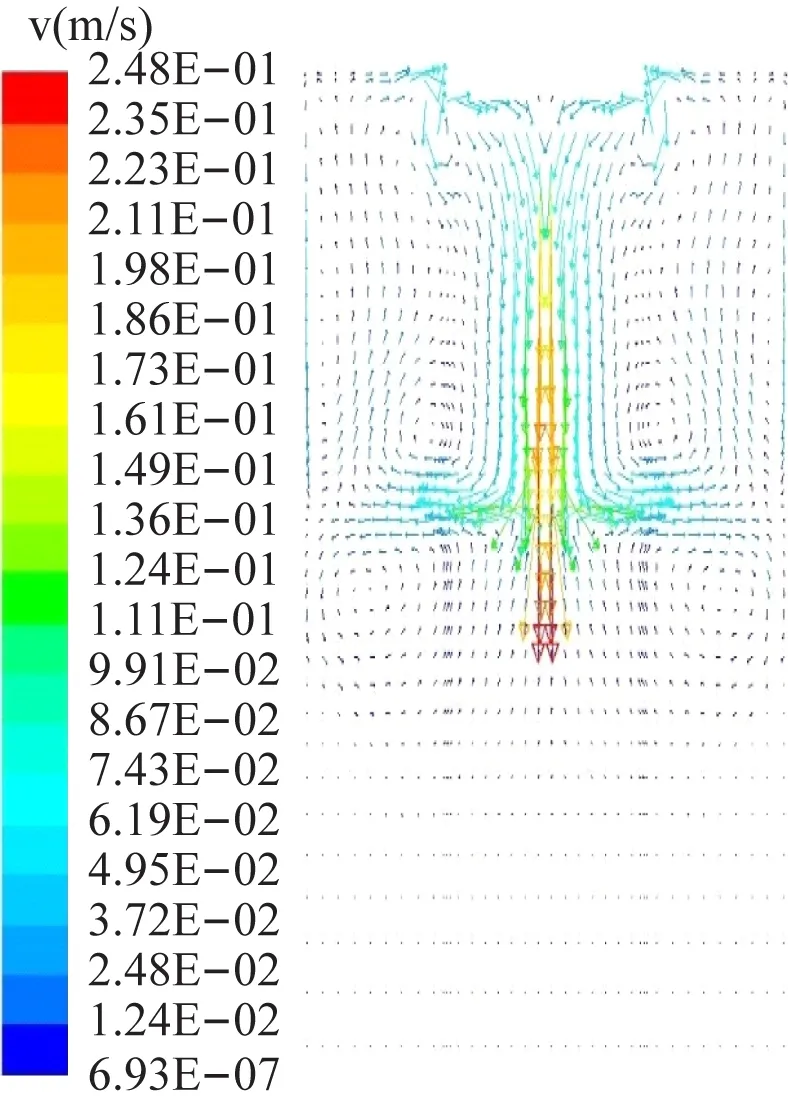
图13 渣池速度场
且在电极底部周围附近速度较大,洛伦兹力的搅拌效果增强,有利于熔池加深及渣池温度均匀化[18];金属熔池内也有漩涡状流动,流动与其上部渣池漩涡流动方向相反,是交界面的渣和滴落的钢液从内向外的流动引起的熔池漩涡,洛伦兹力对金属熔池影响很小;在靠近壁面处存在流速向下的漩涡流动,这是由于近壁面处温度较低内外部密度差形成的浮升力所引起的漩涡流动,该涡流方向与洛伦兹力引起的涡流流动方向相反;在液滴的带动下,在靠近中心处的渣速变大。
图14为金属熔滴在不同时刻形成长大滴落过程。在焦耳热的作用下,自耗电极端头开始熔化,液态金属从端头周围向中心聚集,在重力、表面张力以及洛伦兹力的的共同作用下形成熔滴。熔滴经过长大、脱离母体、分散成小熔滴、缓慢穿透渣层等过程进入到金属熔池,并在渣金界面引起扰动。

t=1st=1.2st=1.3st=1.4st=1.5s
图14熔滴滴落过程
4.3 温度场及凝固
从计算中可知传热过程在1 840 s之后基本趋于稳定,图15为1 848 s时的温度场。由于焦耳热的不同,造成金属域和渣域温度场差距很大,在电极底端周围电渣温度较高,另外由于洛伦兹力引起的漩涡流动使得渣池上部电极下方保持一个较高温度区域,这样有利于电极熔化。在金属熔池下方钢锭区域,金属内部传热为导热,壁面与外界传热为对流,等温线呈阶梯状变化,钢锭底部周边温度最低。图16为1 848 s时金属熔池剖面形貌图,熔池深度约40 mm,从中心到壁面凝固边界由两端弧线组成,在靠近壁面处弧线缓慢降低,拐点之后弧度变大,中心部位较平几乎没有弧度。

图15 熔池温度场图16 金属熔池剖面形貌图
5 结 语
电渣重熔的流场和温度场数值计算,其重点是如何解决由电磁场引起的洛伦兹力和焦耳热对流动和传热的影响。文中应用FLUENT软件的MHD模型中在流动导体内外加磁场法,求解由于磁流体运动而产生的附加磁场传输方程,并将洛伦兹力和焦耳热分别作为源项加入的动量方程和能量方程中。其外部磁场由ANSYS软件通过矢量磁位法计算得到,使用插值法或加权法编写磁场数据转换程序导入到MHD模型中。使用VOF模型进行渣金界面跟踪,渣池热浮升力采用Boussinesq模型,用焓-多孔介质法处理金属凝固模糊区,最后进行多方程同时耦合求解。
计算结果表明,由于磁流体运动引起的附加磁场很小很小,可以忽略不计,所以计算电渣重熔的电磁场时可以不考虑速度效应;渣池内流动主要受洛伦兹力的影响,热浮升力只对近壁面处流动产生影响;电磁场产生的焦耳热在渣域远远大于金属域,渣池大量的焦耳热足以熔化自耗电极,形成稳定的金属熔滴不断滴落;非稳态计算在1 840 s之后在温度场接近稳定,金属熔池形成稳定的凝固边界。
参考文献(References):
[1]姜周华,陈旭,董艳伍,等.电渣冶金技术的创新与发展[J].世界金属导报,2015,11(3):1-5.
[2]李小孟,刘立,赵俊学,等. 电渣重熔冶金过程炉渣粘度性能的研究[J].金属世界,2015(5):56-59.
[3]Eremin E N, Zherebtsov S N, Gritsevich V N. Usingcast electroslag blanks instead of forging in flange production [J]. Chemicaland Petroleum Engineering,2003,39:7-8.
[4]王春光,葛锋,张玉碧,等. 工艺参数对电渣重熔凝固过程的影响综述[J]. 铸造技术,2013,34(10):1321-1323.
[5]张华,关洋,陈瑞,等. 电渣熔铸导叶数值模拟技术研究[J].铸造,2013,62(7):637-640.
[6]梁强,陈希春,付锐,等. 电流对GH4169合金电渣重熔过程影响的数值模拟研究[J].铸造技术,2011,32(9):1252-1256.
[7]DILAWARI A H, SZEKELY J. A mathematical model of slag and metal flow in the ESR process [J]. Metallurgical Transactions B,1977,8B (6):227-236.
[8]Kelkarl K M, Patankarl S V, Srivatsa S K.Computational modeling of electro slag remelting (ESR) process used for the production of high-preformance alloys[C]//Proceedings of the 2013 International Symposium on Liquid Metal Processing and Casting. USA:Wiley, 2013:1-10.
[9]Fezi K, Yanke J, Krane M J M. Modeling macrosegregation during electrslag remelting of alloy 625 [C]//Proceedings of the 2013 International Symposium on Liquid Metal Processing and Casting. USA:Wiley, 2013:151-158.
[10]张赫,雷洪,耿佃桥,等. 电渣重熔过程传热及凝固组织的数值模拟[J].工业加热,2013,42(6):42-46.
[11]景馨,姜周华,刘福斌,等. 导电结晶器电渣重熔空心钢锭电场和温度场的数值模拟[J].材料与冶金学报,2013,12(3):203-208.
[12]王芳,李宝宽. 电渣重熔过程中的电磁场和Joule热分析[J].金属学报,2010,46(7):794-799.
[13]段吉超,董艳伍,姜周华,等. 工艺参数对电渣重熔过程影响的数值模拟研究[J].江西冶金,2014,34(1):5-8.
[14]刘福斌,李永旺,姜周华,等. 实验室规模和工业规模电渣重熔过程中电磁行为[J].中南大学学报,2015,46(10):3580-3585.
[15]贺铸,蔡辉,刘双,等. 不同熔化速率下的电渣重熔过程数值模拟分析[J].重庆大学学报,2015,46(10):104-110.
[16]王晓花,厉英. 电渣重熔过程渣池流场数值模拟[J].材料与冶金学报,2014,13(2):133-136.
[17]刘艳贺,贺铸,刘双,等. 电渣重熔过程中电磁与流动及温度场的数值模拟[J].过程工程学报,2014,14(1):16-21.
[18]梁强,陈希春,郭汉杰. 熔速对GH4169合金电渣重熔凝固过程参数影响的数值模拟研究[J].铸造技术,2013,34(8):1016-1020.
[19]唐建军,耿茂鹏,饶磊. 电渣重熔中电极熔化过程的模拟研究[J].铸造技术,2010,31(8):1062-1065.
[20]刘喜海,王君卿,贾维国,等. 核电用大型钢锭电渣重熔工艺模拟及生产应用[J].铸造,2010,59(12):1315-1319.
[21]白海军,厉英,李宝宽. 电磁搅拌对电渣重熔钢锭温度场的影响[J].特殊钢,2008,29(1):7-9.
[22]王长周,宋锦春. 电渣重熔炉电极熔化速度对重熔过程的影响[J].冶金设备,2012,4(2):5-8.
[23]Antje RüCKERT, Herbert PFEIFER. Numerical modelling of the electroslag remelting process [J]. Metal,2007,5:22-24.
[24]耿茂鹏,孙达昕.电渣熔铸过程控制与模拟仿真[M].北京:冶金工业出版社,2008.
[25]Moreau R. Magnetohydrodynamics[M]. Kluwer Academic Publishers. 1990.
[26]阎照文.ANSYS工程电磁分析技术与实例详解[M].北京:中国水利水电出版社,2008.
[27]Jardy A, Ablitzer D, Wadier J F. Magnetohydrodynamic and thermal behavior of electroslag remelting slags[J]. Metall Mater Trans, B 22B(1991):111-120.
[28]韩丽辉,于春梅,冯根生. 数值模拟质子交换膜燃料电池的方法[J].实验技术与管理,2014,31(8):42-43.
[29]胡进,孙本良,李成威,等.钢液密度对连铸中间包流场影响的数值模拟[J].冶金能源,2008,27(6):12-14.
