环渤海经济圈资本流动水平测度
2018-04-11杨贵军杨鸿海秦泽西
杨贵军,杨鸿海,秦泽西
(天津财经大学 中国经济统计研究中心,天津 300222)
0 引言
资本的有效流动能提高生产要素的配置效率,驱动经济均衡增长。环渤海地区作为我国北方规模最大的经济区,承担着发展北方经济乃至振兴全国经济的重任。然而,环渤海区域规划发展的起步较晚,区域经济发展需要一个过程。在这样背景下,对环渤海经济圈的资本流动现状进行深入了解,有针对性地改善资本有效流动,对提高地区生产要素的配置效率和促进地区经济增长具有重要意义。
在理论上,很难直接测度资本流动。现有的文献对资本流动测度都采用了间接办法[1-9]。在实际应用中,运用FH模型容易忽略储蓄和投资的空间相关性。本地区的储蓄和投资都会受到邻近地区储蓄和投资的影响,样本数据不再满足独立性与匀质性的假定。针对环渤海地区的投资和储蓄,空间效应是指环渤海经济圈城市的投资率或储蓄率的相互依赖、相互作用。各城市的投资率或储蓄率之间存在空间相关性。忽略空间相关性,直接采用FH模型分析储蓄与投资之间的相关关系,分析结果将会出现不可忽视的偏误。
本文将储蓄率和投资率的空间相关性纳入到FH模型中,放宽样本数据的独立性与匀质性的假定,描述地区资本流动。将该模型用于测度环渤海地区的资本流动性。利用环渤海经济圈的经济数据,分析城市的储蓄率和投资率的空间相关性,运用FH广义空间模型进行经验分析。
1 含空间相关性的FH广义空间模型
Feldstein和Horioka(1980)[1]利用OECD国家的储蓄率和投资率的相关程度,描述该地区的资本流动性。FH模型简单,并具有较好的扩展性,便于分析资本流动性的影响因素和影响程度。银行存贷款之间相关性和储蓄与投资之间的相关性具有相似的变化趋势[10]。本文选择各城市金融机构贷款资金存量除以GDP作为投资率,各城市金融机构存款资金存量除以GDP作为储蓄率,选择的FH模型为:

其中,L为金融机构贷款资金存量,D为金融机构存款资金存量,Y为相应的生产总值GDP。L和D分别与Y的比值代替投资率和储蓄率。如果FH模型(1)的β数值较大,投资率和储蓄率的相关性高,意味着投资主要来自于本地的储蓄,资本在地区之间的相互流动小。如果β数值较小,投资率和储蓄率的相关性小,意味着本地的投资并非主要来自于本地的储蓄,资本在地区之间的相互流动性高。由投资率和储蓄率的相关性决定的β数值大小能够反映地区的资本流动性。FH模型(1)没有考虑投资率和储蓄率的空间相关性。然而,环渤海地区的投资率的空间相关性和储蓄率的空间相关性都是显著的。FH模型(1)需要修正,引入这两个变量的空间相关性。
由于FH空间误差模型只能考虑储蓄率的空间误差效用,FH空间滞后模型只能考虑投资率的空间相关性。两个模型都不能同时反映投资率和储蓄率的空间相关性。因此,本文选用广义空间模型[11]。FH广义空间模型为:
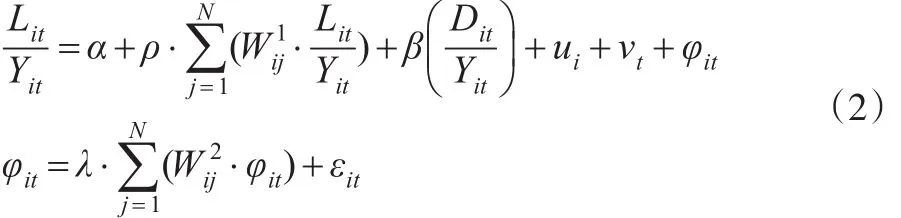
其中,ui为截面固定效用项,vt为时间固定效用项。ρ是空间滞后项的系数,度量地区之间的互相影响程度,λ是空间误差项系数,代表回归残差之间的空间相关程度。λ显著不为0,意味着其他潜在变量会对地区投资率产生间接的空间溢出效应。φit为特异误差项,代表可能产生空间效应的不可观测因素。εit为随机误差项。和分别为空间滞后项的权重矩阵与空间误差项的权重矩阵。这里,没有充分的信息判断和是否一致。采取简化处理方法,选择,约定空间滞后项与空间误差项发生逻辑是一致的,不再考虑其所代表不同的空间效应。权重矩阵有两种形式,分别是一阶邻接权重矩阵和逆距离权重矩阵。由式(2)可以看出,当ρ=0,λ≠0时,FH广义空间模型变为FH空间误差模型:
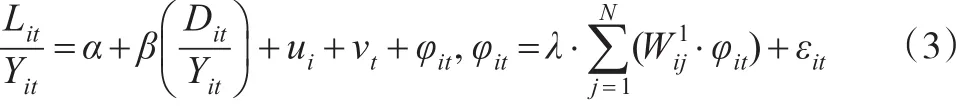
该模型只能考虑储蓄率的空间误差效用。而当ρ≠0,λ≠0时,FH广义空间模型变为FH空间滞后模型:

该模型只能考虑投资率的空间相关性。
为了比较环渤海经济圈资本流动,用两种权重矩阵进行计算和比较。一阶邻接权重的形式为:

一阶邻接权重约定空间相关性的大小取决于地区是否相邻。某城市与其相邻城市均具有相同的相关性,与其不相邻城市的相关性均为0。这个约束条件比较强,与客观事实存在差异。相比较,利用距离信息的逆距离权重矩阵具有更合理的解释。逆距离权重矩阵约定空间相关性取决于两城市的距离,两城市的距离越近则空间性越强。本文采用中国区域经济研究的做法计算权重[12],令dij代表城市i和城市j之间依据两者的经度和纬度位置测算的地表距离。则权重的赋值规则为wij=1/dij。约定对于i=j,wij=0。地区的经度和纬度位置选自谷歌地图。
2 空间相关性检验
本文选取2003—2015年环渤海经济圈城市的数据,数据来源于各省区统计年鉴。为了检验环渤海经济圈城市的投资率和储蓄率的空间相关性,采用全局Moran’s I统计量,其定义为:

其中,xi表示第i个城市的观测值,为环渤海经济圈的城市数。Wij为空间权重矩阵,计算过程中空间权重矩阵采用了基于Queen原则的一阶邻接权重和逆距离权重两种方式进行计算。采用标准化统计量Z(I)的p检验值来检验全局Moran’s I指数的显著性水平,其中Z(I)的计算公式为:

2003—2015年环渤海经济圈城市的投资率与储蓄率的Moran’s I指数如表1所示。
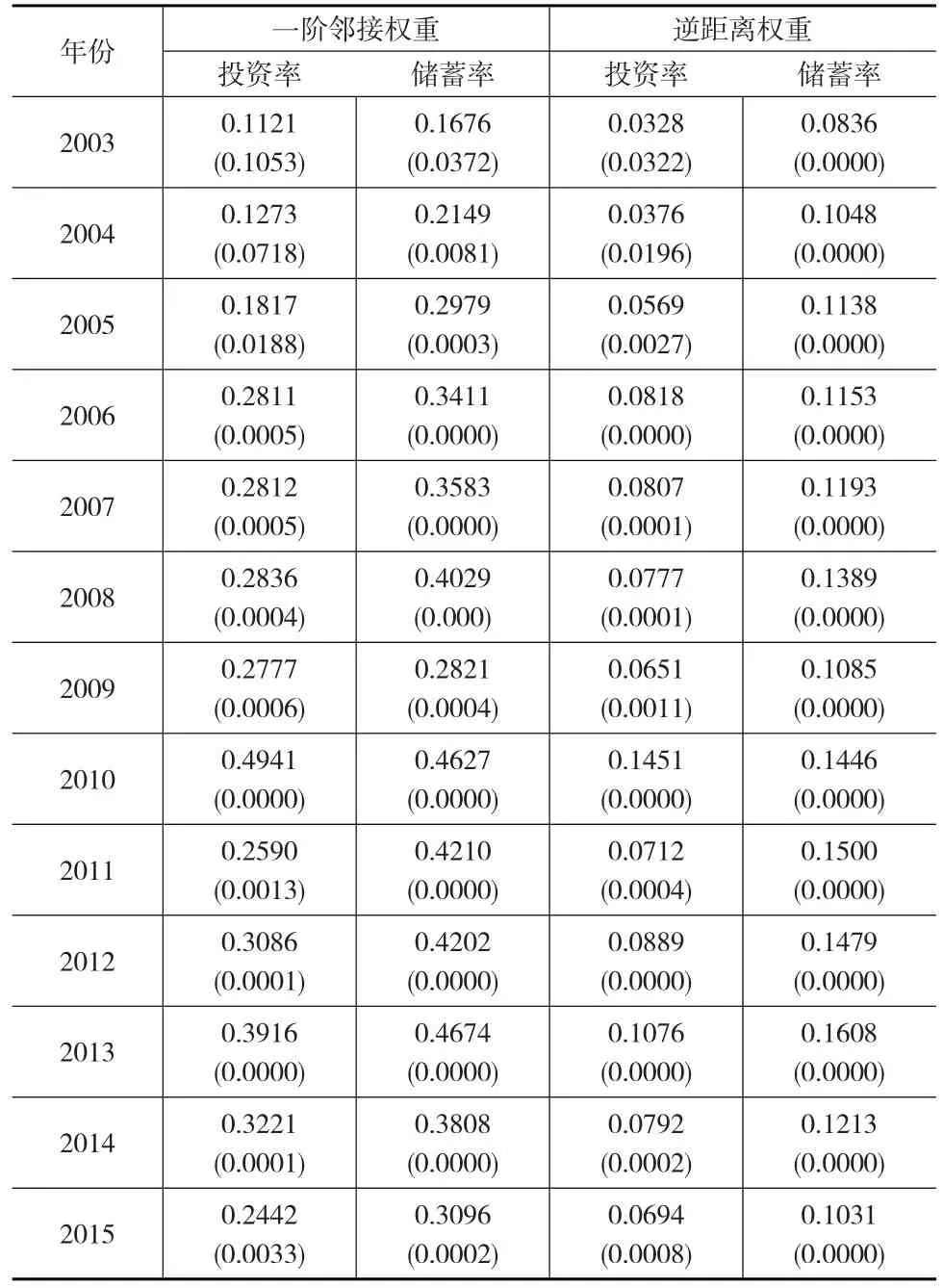
表1 环渤海城市的投资率与储蓄率的Moran’s I指数
表1的第2列给出在一阶邻接权重下城市投资率的Moran’s I指数及其显著性水平。表1显示,环渤海经济圈城市投资率的Moran’s I指数都是正的,说明环渤海经济圈城市的投资率存在正向的空间相关性。其中除了在一阶邻接权重下2003年和2004年Moran’s I指数的显著性水平为0.10和0.07相对较低,其余各年Moran’s I指数的显著性水平较高,反映了城市投资率具有较强的空间相关性。
表1的第4列给出在逆距离权重下城市投资率的Moran’s I指数及其显著性水平。表1显示,在逆距离权重下环渤海经济圈城市投资率的Moran’s I指数也都是正的,说明环渤海经济圈城市的投资率存在正向的空间相关性。在显著性水平0.05下,各年Moran’s I指数都是统计显著的,反映了城市投资率具有较强的空间相关性。在逆距离权重下各年Moran’s I指数都比在一阶邻接矩阵下的指数小。
表1的第3列和第5列分别给出了在一阶邻接权重下和在逆距离权重下储蓄率的Moran’s I指数及其显著性水平。表1显示,环渤海经济圈城市储蓄率在一阶邻接权重下和在逆距离权重下的Moran’s I指数都是正的,说明环渤海经济圈城市储蓄率也存在正向的空间相关性,显著性水平一直较高,反映了城市投资率的空间相关性都是显著的。相比较,在逆距离权重下各年Moran’s I指数都小于在一阶邻接矩阵下的指数。
综上所述,2010年城市投资率的空间相关性高于城市储蓄率的空间相关性。其余年度城市储蓄率的空间相关性高于城市投资率的空间相关性。城市投资率和城市储蓄率的空间相关性是FH模型的重要内生问题,不能忽略,需要相应处理,否则可能会造成FH模型给出结论的偏误过大。
3 环渤海城市的FH广义空间模型估计
本文利用环渤海经济圈2003—2015年城市投资率和储蓄率对传统FH模型和FH广义空间模型进行估计,结果见表2。表2的第2列给出了FH模型的估计结果,第3列和第4列分别给出了在一阶邻接权重下和逆距离权重下的FH空间滞后模型的估计,第5列和第6列分别给出了在一阶邻接权重下和逆距离权重下的FH空间误差模型的估计,第7列和第8列分别给出了在一阶邻接权重下和逆距离权重下的FH广义空间模型的估计。

表2 FH广义空间模型的估计结果
由表2可知,4个模型的拟合优度都高于0.55,拟合FH模型的AIC值大,其他6个拟合模型的AIC都小。在一阶邻接权重下,拟合模型的AIC最小的是FH空间误差模型,其拟合优度R2也最大。在逆距离权重下,拟合模型的AIC最小的也是FH空间误差模型,其拟合优度R2大于拟合FH空间滞后模型,但略小于拟合FH广义空间模型。相比较FH空间误差模型对数据拟合更充分。
在一阶邻接权重下,FH空间滞后模型的参数ρ的估计约为0.3,而FH广义空间模型的参数ρ的估计约为0.03,但统计不显著。FH空间误差模型的参数λ的估计与FH广义空间模型的参数ρ的估计接近,约等于0.4。在逆距离权重下,FH空间滞后模型的参数ρ的估计约为0.5,而FH广义空间模型的参数ρ的估计约为负值,但统计不显著。FH空间误差模型的参数λ的估计0.72略小于FH广义空间模型的参数ρ的估计0.79。
在一阶邻接权重下和在逆距离权重下,FH空间滞后模型的β估计为0.5684和0.5560,FH空间误差模型的β估计为0.6059和0.6058,FH广义空间模型的β估计为0.6070和0.6048,两个条件下的估计值差异很小,FH空间误差模型和FH广义空间模型的β估计更接近。相比较,FH模型的β估计为0.4732,小于其他模型的估计结果,可能被低估,FH空间误差模型和FH广义空间模型的β估计结果更合理。其估计结果也说明环渤海经济圈储蓄与投资有一定的相关性,资本流动性较弱。这一结果也符合人们对环渤海城市群经济发展水平相对落后于长三角城市群和珠三角城市群的经济发展水平的判断。这也说明,FH模型应该引入空间相关性进行修正的必要性。
4 分阶段FH广义空间模型分析结果
为了分析这些年的资本流动水平变化,本文分别建立2003—2007年与2011—2015年间的资本流动模型。其中,不考虑2008—2010年的时间段,是因为这期间经济波动大,也为了更很好地进行前后时间段的对比。表3给出了FH模型和FH广义空间模型的估计结果,表3的列结构同表2。
表3显示,在一阶邻接权重下,对于2003—2007年的FH空间滞后模型的R2小于0.5,而FH空间误差模型和FH广义空间模型的R2接近0.6,FH空间误差模型的R2最大,为0.582。三个拟合模型的AIC都小于-250,其中FH广义空间模型的AIC最小,为-268.808。三个模型拟合充分。FH空间滞后模型的参数ρ的估计约为0.383,而FH广义空间模型的参数ρ的估计约为-0.427,但统计不显著。FH空间误差模型的参数λ的估计为0.481,FH广义空间模型的参数ρ的估计为0.722。FH空间滞后模型的β估计为0.462,FH空间误差模型的β估计为0.476,FH广义空间模型的β估计为0.417,这些估计值差异不大。
在逆距离权重下,对于2003—2007年的FH空间滞后模型的R2小于0.5,而FH空间误差模型和FH广义空间模型的R2接近0.6,FH广义空间模型的R2最大,为0.592。三个拟合模型的AIC都小于-300,其中FH空间误差模型的AIC最小,为-304.65。三个模型拟合充分。FH空间滞后模型的参数ρ的估计约为0.730,而FH广义空间模型的参数ρ的估计约为-0.368,但统计不显著。FH空间误差模型的参数λ的估计为0.803,FH广义空间模型的参数ρ的估计为0.871。FH空间滞后模型的β估计为0.449,FH空间误差模型的β估计为0.456,FH广义空间模型的β估计为0.450,这些估计值差异很小。
综合上述分析,相比较可知,FH模型的β估计为0.491,大于其他模型的估计结果,差异小,FH空间滞后模型、FH空间误差模型和FH广义空间模型的β估计结果更好被接受。其估计结果也说明环渤海经济圈储蓄与投资的空间相关性逐渐增强,存在一定程度的资本流动。这一结果也符合人们的直观。

表3 分时段环渤海经济圈城市FH广义空间模型的估计结果
表3显示,在一阶邻接权重下,对于2011—2015年的三个模型的R2都大于0.6,FH空间误差模型的R2最大,为0.670。三个拟合模型的AIC都小于-150,其中FH空间滞后模型的AIC最小,为-167.114。三个模型拟合充分。FH空间滞后模型的参数ρ的估计接近于FH广义空间模型的参数ρ的估计。FH空间误差模型的参数λ的估计为0.356,FH广义空间模型的参数ρ的估计为-0.064,统计不显著。FH空间滞后模型的β估计为0.572,FH空间误差模型的β估计为0.604,FH广义空间模型的β估计为0.561,这些估计值差异不大。
班主任教育失误后,要根据实际情况,有针对性地找学生谈心,向学生解释清楚严厉批评其是因为老师面对的不是一位学生,而是全班几十位学生,老师想通过这件事使全班学生都受到教育,也许批评重了一些,希望其能谅解。通过讲道理,循循善诱,动之以情、晓之以理,帮助学生消除心理障碍,提高思想认识,理解班主任的工作,愉快地接受教育,尽可能减少或消除内心的不满。
在逆距离权重下,对于2011—2015年的三个模型的R2大于0.6,而FH空间误差模型的R2最大,为0.670。三个拟合模型的AIC都小于-150,其中FH空间滞后模型的AIC最小,为-160.974。三个模型拟合充分。FH空间滞后模型的参数ρ的估计约为0.4528,而FH广义空间模型的参数ρ的估计约为0.422。FH空间误差模型的参数λ的估计为0.696,FH广义空间模型的参数ρ的估计为0.303。FH空间滞后模型的β估计为0.559,FH空间误差模型的β估计为0.579,FH广义空间模型的β估计为0.568,这些估计值差异很小。
综合上述分析,FH模型的β估计为0.483,小于其他模型的估计结果。FH空间滞后模型、FH空间误差模型和FH广义空间模型的β估计结果更好被接受。其估计结果也说明环渤海经济圈储蓄与投资的空间相关性逐渐增强,存在一定程度的资本流动。这一结果也符合人们的直观。
同时由表3可以看出,在2003—2007年期间环渤海经济圈资本流动水平高于2011—2015年的整体水平,说明在此期间借助于北京奥运的机遇各地增加投资,且随着外商资本注入的增加致使环渤海地区金融资本流动的速度加快,使得环渤海经济圈资本流动水平有所提高,由美国次贷金融危机而引起的全球性金融危机致使中国不可避免的受到了牵连,而环渤海地区资本流动也意料之中的发生了下降,反映在投资-储蓄相关系数上的变化是在邻接矩阵和逆距离矩阵两种情况下2011—2015年的β值都大于2003—2007年的β值。
5 结束语
本文在一阶邻接权重矩阵和逆距离权重矩阵两种情形下,利用FH广义空间模型对环渤海经济圈资本流动水平进行了测度,发现环渤海经济圈在2003—2015年整个时间段内,资本流动水平较弱。分时间阶段分析结果表明,2003—2007年期间环渤海经济圈资本流动性大于2011—2015年金融危机发生后的资本流动水平。
参考文献:
[1]Feldstein M,Horioka C.Domestic Saving and International Capital Flows[J].Economic Journal,1980,90(358).
[2]Feldstein M,Bacchetta P.National Saving and International Investment[M].Chicagao:University of Chicagao Press,1991.
[3]Penati A,Dooley M.Current Account Imbalances and Capital Formation in Industrial Countries,1949-81[J].Staff Papers,1984,31(1).
[4]Murphy R G.Capital Mobility and the Relationship Between Saving and Investment Rates in OECD Countries[J].Journal of international Money and Finance,1984,3(3).
[5]Bayoumi T.Saving-Investment Correlations:Immobile Capital,Government Policy,or Endogenous Behavior?[J].Staff Papers,1990,37(2).
[6]Tesar L L.Savings,Investment and International Capital Flows[J].Journal of International Economics,1991,31(1-2).
[7]Bayoumi T A,Rose A K.Domestic Savings and Intra-National Capital Flows[J].European Economic Review,1993,37(6).
[8]Iwamoto Y,Wincoop E.Do Border Matter?Evidence from Japanese R egional Net Capital Inflows[J].International Economic Review,2000,41(1).
[9]Yoshihiro H,Shigeyuki H.Saving-Investment Relationship and Capital Mobility:Evidence from Chinese Provincial Data,1980-2007[J].Mpra Paper,2009.
[10]Genevieve B D,Wei S J.Can China Grow Faster?A Diagnosis of the Fragme-ntation of Its Domestic Capital Market[R].IMF Working Paper,2004,(4).
[11]Lee L F,Yu J H.Estimation of Spatial Autoregressive Panel Data Models With Fixed Effects[J].Journal of Econometrics,2010,154(2).
[12]钟水映,李魁.人口红利,空间外溢与省域经济增长[J].管理世界,2010,(4).
