基于排序误差长度的综合评价指标体系检验方法探讨

刘渝妍，刘渝琳，邱 莎，杨 流

（1.昆明学院 信息技术学院，昆明 650214；2.重庆大学a.人口资源环境研究中心；b.经济与工商管理学院，重庆 400044）

0 引言

分析和评价一个国家的人口均衡状况如何，除了进行定性的描述和分析之外，更重要的是需要对其进行定量的描述和分析，指标体系的建立是进行评价的前提和基础，构建人口均衡型社会评价指标体系的主要目的是，动态地发现人口社会发展过程中出现的矛盾，从比较结果中评价失衡的程度，用结果纠正过程和结构。

人口均衡型社会评价指标体系（见后文表1）是在大量文献[1-7]研究基础上利用TF-IDF（客观）自动提取关键词[8]和OOA（主观）提取指标类进行指标选择；通过OOA构建指标体系层次结构[9，10]；通过层次分析法（主观）和独立权系数法（客观）、变异系数法（客观）进行组合确定权重[11，12]。在构建的指标体系基础上，本文将通过灰关联序与综合指数结果排序的排序平均误差长度来检验所建立评价指标体系的合理性。

1 基于灰色关联度的灰关联序

灰色系统理论认为，用行为因素序列的几何接近度可确定因子之间的影响程度，并将这种因素之间发展趋势的相似或相异程度称为灰色关联度，用来描述因素间关系的强弱、大小和次序，若样本数据反映出的两因素变化的态势（方向、大小和速度等）基本一致，则它们之间的关联度较大；反之，关联度较小。研究两个序列绝对增量间的关系通常用两条折线间所夹的面积大小来衡量两序列的关联性大小，即用灰色绝对关联度进行衡量[13]。

定义1：设X为系统对象，设i为时间序号（i=1,2,…,t），则Xi为系统对象的时间序列；设k为指标序号（k=1,2,…,n），称Xi=(xi(1),xi(2),…,xi(n))为对象Xi的指标序列，则xi(k)为对象Xi关于第k个指标的观测数据。

定义2：若系统对象指标序列Xi=(xi(1),xi(2),…,xi(n))，X0=(x0(1),x0(2),…,x0(n))的始点零化像（利用下文的始点零化像变换算子D0）分别为：

设：

ε0i，称ε0i为X0与Xi的灰色绝对关联度。

定义3：称反映系统特征行为的数据序列为参考序列，称影响系统行为的因素组成的数据序列为比较序列。

定义4：设X0为系统特征行为序列，Xi和Xj为相关因素行为序列，若ε0i≥ε0j，则称因素Xi优于因素Xj，记为Xi≻Xj。称“≻”为由灰色关联度导出的灰关联序。

由定义4可知，若X0为系统特征行为的最优参考指标序列，Xi（i=1,2,…,t）为系统对象的时间指标序列，将t个时间指标序列对最优参考指标序列X0的关联度按大小顺序排列起来，即可组成关联序，用以反映各时间指标序列对于最优参考指标序列的“优劣”关系。其中，最优参考指标序列的获取方法，可根据国际标准、国家标准、行业标准、社会标准等直接获取，对于没有参考标准的指标，在进行标准化处理时，因各指标的取值限定在[0，1]区间，各指标的最优值可取为1。

2 变换算子定义及标准化变换原则

在进行关联分析之前，由于系统中各指标因素的物理意义不同，导致指标数据的量纲也不一定相同，难以进行指标间直接对比分析。同样，在进行综合评价时，各个指标对综合评价的影响方向不同，有正指标、逆指标和适度指标/区间指标之分，对于逆指标和适度指标/区间指标，需调整方向使其与正指标的发展趋势相一致。基于此，本文可利用变换算子对原始指标数据进行标准化变换处理。

定义5：设j为指标变换算子序号，称D={Dj|j=1,2,...,m}为灰色关联指标变换算子集。对于XiDj=(xi(1)dj,xi(2)dj,…,xi(n)dj)，存在下列变换算子。

（1）初值化指标变换算子D1

（2）效益型指标变换算子D2

XiD2=(xi(1)d2,xi(2)d2,…,xi(n)d2)

（3）成本型指标变换算子D3

XiD3=(xi(1)d3,xi(2)d3,…,xi(n)d3)

（4）固定型指标变换算子D4

（5）区间型指标变换算子D5

XiD5=(xi(1)d5,xi(2)d5,…,xi(n)d5)

其中：

称D5为区间算子。

（6）始点零化像指标变换算子D0

其中：xi(k)d0=xi(k)-xi(1)，称D0为始点零化像指标算子。

根据定义5，可利用灰色关联算子集D中的算子，根据指标的不同性质对指标数据进行标准变换，并将各指标的取值限定在[0，1]区间，其数据变换流程如图1所示：

图1 指标数据标准变换流程

3 灰关联序及综合评价的计算

3.1 灰关联序的实现步骤

第一，确定反映系统特征行为的参考序列X0和影响系统行为的比较序列Xi。

第二，利用相关变换算子使系统参考序列和比较序列标准化。

第三，分别计算参考序列与每一个比较序列间的关联度。

①求始点零化像

②分别计算|s0|,|si|,|si-s0|

③计算出X0与Xi的灰色绝对关联度

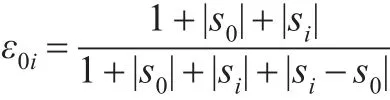
第四，根据各关联度导出灰关联序。

3.2 综合评价的实现流程

综合评价是在确定一套合理的评价指标体系基础上，对评价系统对象各项指标个体指数加权平均计算出综合值，用以反映各评价系统对象综合质量的一种评价方法。根据定义1，第i（i=1,2,…,t）个对象的综合评价指数=，k为指标序号 (k=1,2,…,n)。综合评价的实现流程如下页图2所示。

4 排序平均误差长度定义

如何验证综合评价对象排名的合理性，以保证n个系统对象评价结果的准确性?其本质就是如何验证指标体系中权重设置的合理性。本文提出排序平均误差长度的概念来检验权重设置的合理性。

图2 综合评价的实现流程

定义6：设Pi为第i个系统对象在综合评价中的排名，Gi为第i个系统对象在灰关联序中的排名，| |Pi-Gi为第i个系统对象的排名差异。

定义7：设n为评价系统对象数，在综合评价排名与灰关联序的排名中，排序平均误差长度（Average Error of Length）为：

根据定义7，平均误差长度具有以下性质：

（1）平均误差长度AEL反映评价的一致性程度。在指标个数和观测值不变的情况下，以灰关联序的排名为基准，综合评价的排名平均波动不会超过AEL。平均误差长度可作为比较综合评价与灰关联序对评价系统对象排序结果差异性的衡量标准。

（2）对于给定的ε≥0（通常取ε=0.3），若AEL≤ε，说明综合评价对n个系统对象的排序是符合现实的，权重值的设置是合理的，否则需重新设置权重。

5 人口均衡型社会综合评价指标体系检验

人口均衡型社会评价指标体系旨在准确测度和把握人口均衡型社会建设进程与效果，是“人口均衡型社会”建设过程中不可或缺的技术支持和保障。通过指标体系的评价，为人们正确认识人口均衡社会、正确决策，达到社会可持续发展、经济福利可均衡增长提供了科学的依据。本文利用排序平均误差长度对构建的人口均衡型社会评价指标体系（如表1所示）进行检验。

数据主要来自于中国人民共和国国家统计局《中国统计年鉴》，包括人口、教育、卫生、就业人员和工资、国民经济核算、人民生活、固定资产投资、社会服务、城市概况、公共管理保障和其他、农业、运输和邮电、能源、资源和环境、财政等多个部分。

人口均衡型社会综合指数排序与人口均衡型社会灰关联序计算的主要VB程序略，如需要可向作者索取。

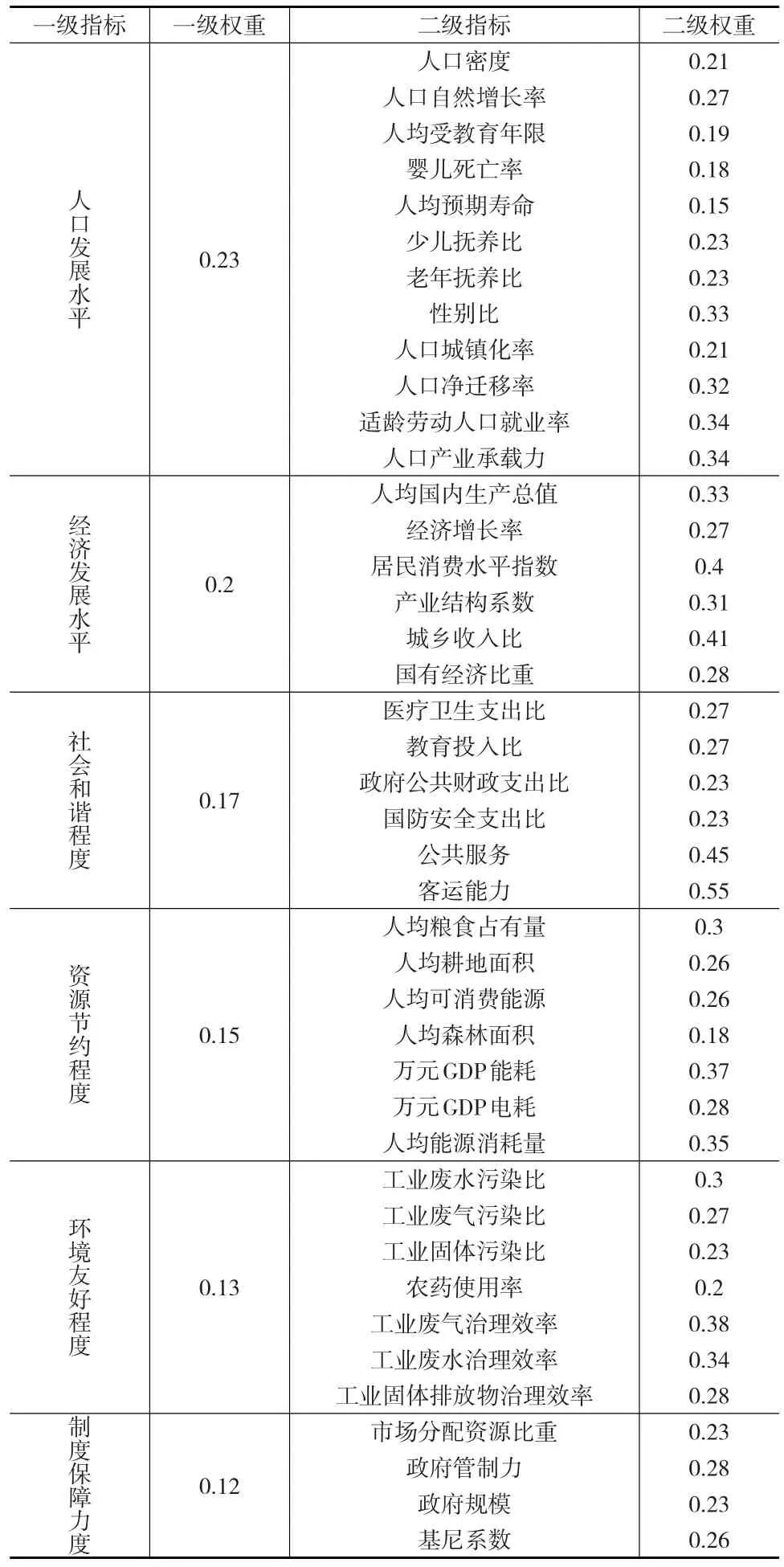
表1 人口均衡型社会评价指标体系

5.1 人口均衡型社会综合评价排序

根据表1，人口均衡型社会综合评价指数（the comprehensive Evaluation index of Population Balance type Society）分别表示42个相关因素，wi(i=1,2,...,42)表示对应的权重。分别计算1993—2013年人口均衡型社会综合评价指数，评价排序结果如下页图3所示。

根据综合评价结果，我国人口均衡型社会的均衡程度稳定上升。

图3 1993—2013年人口均衡型社会综合评价指数

5.2 灰关联序

设Y为系统特征行为序列并取理想最优特征值为{yi|i=1,2,...,42,yi=1}，对1993—2013年的数据进行关联度计算，得到关联序如图4所示。

图4 1993—2013年人口均衡型社会灰关联序

5.3 基于排序平均误差长度分析

整理EPBS模型和灰色关联度模型对1993—2013年人口均衡情况进行排序的结果，得到表2。

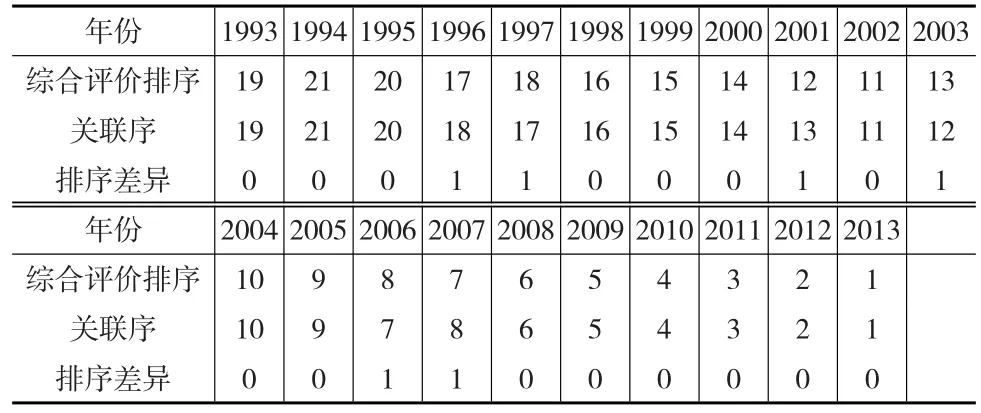
表2 1993—2013年人口均衡型社会均衡程度排序

随着国家在经济、能源、人口等方面实施可持续发展战略，人口均衡型社会的均衡程度越来越好。在EPBS模型中一级指标共有六个，即人口发展水平、经济发展水平、社会和谐程度、资源节约程度、环境友好程度和制度保障力度，对应指标的组合权重分别为0.23、0.20、0.17、0.15、0.13和0.12，其中人口发展水平和经济发展水平所占比重较高，其次是社会和谐程度和资源节约程度，最后为环境友好程度和制度保障力度。

从表2中可以得到，排序误差值为0～1，平均误差长度AEL=（0*15+1*6）/21=0.286＜0.3，两种方法的排序结果基本一致。

在EPBS模型和灰色关联度得到的人口均衡型社会综合评价指数排名中，有3组年份的名次不一致。这三组年份分别是1996—1997年、2001—2003年、2006—2007年。具体分析说明如下：

（1）1996—1997年

采用灰色关联度计算得出的结果是1996年排名18，1997年排名17，而EPBS模型得到的结果是1996年排名17，1997年排名18。1997年和1996年这些因素的数据如表3所示，显然1996年有8个重要指标远远超过1997年的数据。因此最终的结果是1996年人口均衡型社会综合评价指数排名优于1997年的人口均衡型社会综合评价指数排名。

表3 EPBS主要影响因素变化

（2）2001—2003年

采用灰色关联度计算得出的结果是2001年排名13，2003年排名12，而EPBS模型得到的结果是2001年排名12，2003年排名13。这是由于2001年有12个重要指标远远超过2003年的数据，如表4所示。因此最终的结果是2001年人口均衡型社会综合评价指数排名优于2003年的人口均衡型社会综合评价指数排名。

（3）2006—2007年

表4 EPBS主要影响因素变化

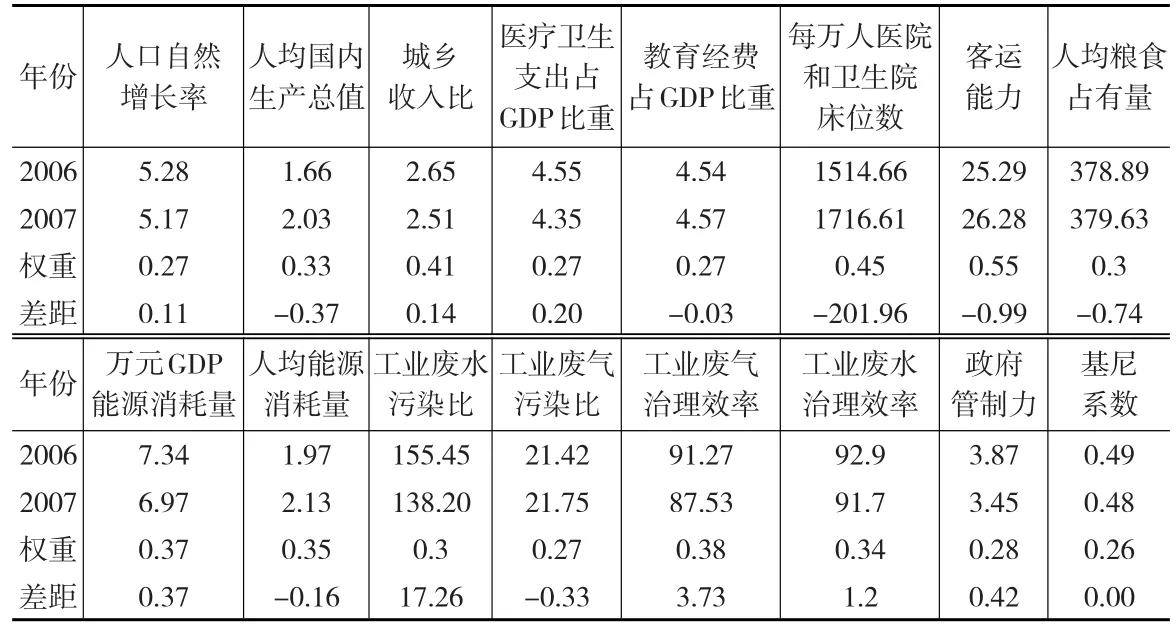
表5 EPBS主要影响因素变化对照表

采用灰色关联度计算得出的结果是2006年排名7，2003年排名8，而EPBS模型得到的结果是2006年排名8，2007年排名7。2006年和2007年这些因素的数据由下页表5所示，显然2006年有7个重要指标远远低于2007年的数据。值得注意的是2006年每万人医疗卫生机构床位数这一指标远远低于2007年的指标数，因此最终的结果是2007年人口均衡型社会综合评价指数排名优于2006年的人口均衡型社会综合评价指数排名。

6 结束语

排名结果之所以出现较小的波动，是由于灰色关联度模型是相对于最优序列的关联排名，EPBS模型中权重的设置融入了专家意见，但排序平均误差长度AEL＜0.3，因此，EPBS模型得到的排名是可靠和准确的。说明表人口均衡型社会评价指标体系是合理的。

参考文献：

[1]人口长期均衡发展课题组.以科学发展为主导构建人口均衡型社会[J].人口研究，2010，(5).

[2]靳玮,徐琳瑜,杨志峰.城市适度人口规模的多目标决策方法及应用[J].环境科学学报，2010，(2).

[3]张双双.我国和谐社会评价体系的建立及实证分析[D].保定：河北大学硕士学位论文，2010.

[4]翟振武.建设人口均衡型社会[J].求是，2013，(23).

[5]周炎炎,王学义.中国人口发展监测指标体系构建及应用研究[J].北京社会科学，2014，(5).

[6]陆杰华,黄匡时.关于构建人口均衡型社会的几点理论思考[J].人口学刊，2010，(5).

[7]刘渝妍.基于灰色定权聚类的软件质量评价模型研究[J].西南大学学报，2008，(5).

[8]刘渝琳，刘渝妍，赵卿.应用本体领域构建FDI效应模型[J].重庆大学学报，2013，(10).

[9]刘渝妍，赵卿，陈媛.基于UML的老年人口生活质量指标体系框架模型设计[J].重庆工学院学报，2005，(10).

[10]刘渝妍,刘渝琳.基于UML与灰色理论的指标体系构建[J].统计与决策，2008，(15).

[11]Liu Y L,Liu Y Y,Wang Z J.Study on Indexes Weighting of the Physical Quality of Life Evaluation of Rural Migrant Workers—Application of Combined Weighting Method Based on AHP and ANN[R].Fourth International Conference on Natural Computation ICNC 2008 Volume 2.

[12]Liu YY,Zhao Q.The Research on the Construction Method of Evaluation Indicator System Based on Software Product Line[R].2011 Eighth International Conference on Fuzzy Systems and Knowledge Discovery，2011.

[13]刘思峰,郭天榜,党耀国.灰色系统理论及其应用[M].北京：科学出版社，1999.