基于贝叶斯后验的网络舆论三角模糊数型危机识别
2018-04-11郭新朋
魏 玲,郭新朋
(哈尔滨理工大学 管理学院,哈尔滨 150000)
0 引言
近年来贝叶斯理论在我国的概率统计领域中快速发展,影响着各行各业的学术研究发展步伐,基于贝叶斯公式而形成的图形化网络——贝叶斯网络(Bayesian Network,BN),利用概率推理方式对一些变量信息进行处理,从而获取概率数据,不仅可以解决不确定性和不完整性的问题,还能够通过概率来推理出相关影响因素之间的潜在关系[1]。依据经验推断结合贝叶斯公式产生的先验概率结果,通常情况下被视为主观概率,而这种概率结果所产生的结论也具有一定的主观色彩,在网络舆论危机的识别过程中,客观性、系统性等特性是必然要求,所以利用贝叶斯理论中的后验概率进行影响因素发生质变的概率统计具有客观性,其主要特性是对先验概率的修正,从而为网络舆论风险分析提供概率统计基础[2]。
本文提出了基于贝叶斯后验的网络舆论三角模糊数型危机识别方法。在三角模糊数型网络舆论危机识别过程中,应用贝叶斯网络的概率推理技术结合贝叶斯理论中的后验概率确定主要网络舆论危机产生的影响因素,利用三角模糊数描述各专家对舆论危机产生影响因素评分的模糊性,文献[3]利用贝叶斯网络与三角模糊数相结合,分析了故障模式属性与危害度之间的关系,但没有进行去模糊处理,存在结果模糊的问题。根据贝叶斯网络中的概率推理及信息数据处理规则对统计的概率进行均值化、去模糊化与归一化,从而确定网络舆论影响因素的危险指数,并对比危险等级划分表确定各影响因素的危险等级。利用模糊综合评价理论中的评语集给出对应影响因素的三角模糊数评语值,对危机影响因素进行加权处理,从而确定网络舆论危机发生等级。
1 理论基础
1.1 贝叶斯网络
贝叶斯网络的概率推理技术最先由Pearl[4]提出,用有向无环图(DAG)表示,能够解决不确定性的、复杂的问题,且贝叶斯公式是该概率网络的理论基础[5],具体定义如下:
定义1:条件概率。假设A、B为一个随机试验中的两个事件,将事件A在事件B发生的条件下的概率称之为条件概率,表示如下:

定义2:全概率公式。若Aj,j=1,…,m,其中m表示m个互不相容的事件,且P(Aj)〉0,j=1,…,m。

定义3:贝叶斯公式。将全概率公式(2)带入条件概率公式(1)中,即可得到贝叶斯公式:

式中,B表示随机试验的结果,P(Ai)为先验概率,P(Ai|B)为后验概率。
由贝叶斯公式可知,后验概率公式获得情况如下描述,假设D是训练对象的集合,且每个训练对象用n维属性向量,基于n维属性向量共划分为m个类,由此得到后验概率计算公式[6]为:

根据贝叶斯理论中的联合概率分布可知,贝叶斯网络中的每个变量(属性)之间存在着一定的关联性,因此可得到如下公式进行条件独立假设:

由公式(5)可知,网络中的每个节点则对应一个变量(属性),当P(Bi|j)P(Aj)>P(Bi|k)P(Ak),1≤k≤m,1≤j≤m,j≠i且j≠k成立时,B属于Aj。
贝叶斯网络存在两种结构,一种是用有向无环图进行表示的结构,其中每个节点表示一种变量(属性),且每个变量之间的弧表示变量(属性)之间存在的因果关系,如图1给出简单贝叶斯网络有向无环图结构。另一种则是条件概率表(Conditional Probability Table,CPT),可用该表表示每个节点变量对父节点变量的所有可能性。

图1 简单贝叶斯网络结构
贝叶斯网络概率推理技术不仅包含将静态和动态结合分析,有效辨析专家经验和问题变化情况的正向推理,还包含后验概率统计得出的结构逆向获取信息的推理方式,找到事件发展变化的原因。由于网络舆论演化过程中的影响因素之间形成的条件概率数据有所缺失,故需将获取的专家评分的先验概率作为研究基础,结合贝叶斯的概率推理技术进一步研究[7]。
(1)正向推理。正向推理是贝叶斯网络概率推理技术中的因果推理,即通过对网络舆论中危机风险影响因素发生的条件概率进行统计,从而对网络舆论危机发生进行预测。
(2)逆向推理。逆向推理在贝叶斯网络概率推理中也是诊断推理,通常指对已知的危机结果,利用逆向推理进行运算,即在计算出先验概率的情况下,得出该变量(属性)的后验概率。
(3)双向推理。双向推理则利用部分正向推理的结果,在逆向推理过程中,对导致危机结果的原因进行逆向推理,从而实现对原因与结果的解释。
在网络舆论危机产生过程中,每个阶段都是不同的状态,通常表现为多阶段与多影响因素。在多阶段中主要包含了网络舆论危机潜伏期、过渡期、爆发期,每个时期相关联的影响因素也是不同的,例如潜伏期中有潜在舆论驱动群体、隐性利益。而网络舆论危机形成的整个周期有着共同的影响因素,政府公信力降低、媒体舆论信息传播失真、网民关注度偏移等。贝叶斯网络的多状态离散处理系统可以将不同的状态进行关联分析,即将每个影响因素之间的界限进行模糊化处理,从而提高分析各影响因素发生概率的准确值。
1.2 三角模糊数
1.2.1 三角模糊数定义
根据传统的三角模糊数理论可知,一个三角模糊数中包含三个可能值,即较低可能值、可能值、较高可能值,按照概率分布函数确定三角模糊数的隶属函数,给定一个随机三角模糊数,且已知 0≤Al≤Am≤Au,则变量b属于˜的隶属度公式为:

1.2.2 三角模糊数运算法则[8]
(1)加法交换律

(4)除法运算

(5)数乘运算(给定任意实数β)

式(9)中,Aj(j=l,m,u)与Bi(i=l,m,u)中至少有一个大于零;式(10)中,Bi(i=l,m,u)大于零。
三角模糊数理论应用于网络舆论危机识别过程,由于网络舆论危机的表现极具模糊化,且依据其三个发展阶段可以看出,影响舆论变质化的因素体现在网民、事件、政府、媒体等类别,因此针对某一个公共事件的网络舆论危机识别的过程中必须依照专家的经验进行初步判断,才能确定贝叶斯网络的危机评定的基础。
由贝叶斯网络的先验概率公式与专家经验结合计算可得,三角模糊数均值化公式如下:

基于上述三角模糊运算法则,给定任意一个正整数η和三角模糊数,则将该三角模糊数去模糊化的公式如下:

给定M位专家的评语,按照下页表1给出的三角模糊数评语值进行如下计算,第i个变量(属性)B的三角模糊数概率矩阵可用,其中j=1,2,…,m。三角模糊数归一化公式如下:

在式(13)与式(14)的联合基础上进行危机等级公式处理,如式(15):

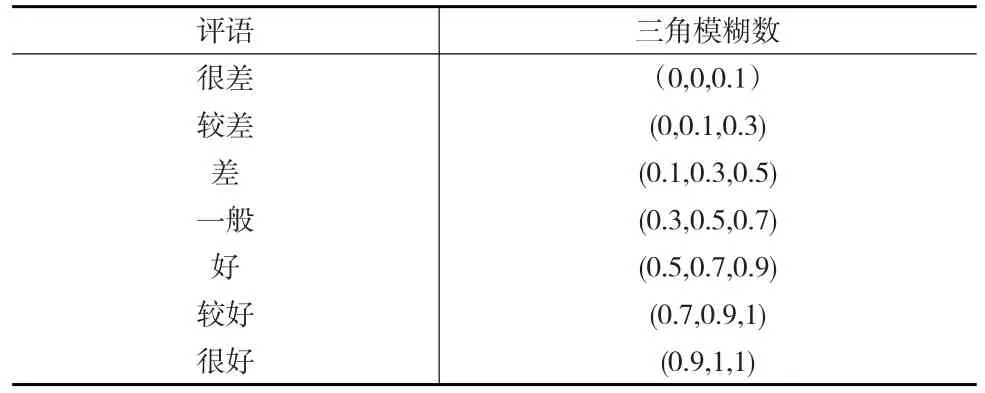
表1 变量危机程度评语及其对应的三角模糊数[9]
2 三角模糊数型网络舆论危机识别
网络舆论在不同的网络平台中已经成为了人们进行及时获取、交流与传递信息的一种方式。本文主要以2016年上半年发生的重大医疗事故事件——“魏则西事件”作为依据进行分析。该事件发生后不仅引起了政府对医疗的关注,还引起了一场网络舆论浪潮,针对医疗机构与百度搜索排名相关讨论大幅度增加,造成的舆论导向群体极化现象也是比较严重的,因此对此事件应用贝叶斯网络结构下的三角模糊数进行网络舆论危机识别是有必要的。
研究过程中向专家群体征求意见,按照专家经验总结分析,并对收集回来的问卷进行模糊化处理,得到具体的评估值,应用于贝叶斯网络后验概率的计算和三角模糊数的确定。问卷获取来源的各个专家群体主要包含医学领域的各大高校教授、互联网竞价排名领域的专家、高校科研管理部门主管以及政府相关处理部门的领导的意见,共发放了150份,回收有效问卷数量为138份。具体的危机识别过程如下:
2.1 网络舆论贝叶斯网络的构建
贝叶斯网络的构建过程中首先需要确定网络中的根节点和叶节点,其次是确定连接变量之间的有向关联弧,因此通过对专家进行调查访问得到表2的网络舆论中主要影响因素及类别,并给出如图2所示的网络结构图。
从图2中可以看出,贝叶斯网络中有5个根节点,其余均为叶节点,且其中包含4个类别节点。其中根节点集合为{b1,b2,b6,b12,b14},叶节点为“网络舆论”,而其余均为中间节点。
2.2 模糊概率计算及处理

图2 网络舆论贝叶斯网络结构

表2 网络舆论贝叶斯网络结构指标说明
依据动态分析理论,确定模糊概率需要将同一影响因素在不同的时间段内产生的不同结果进行统计,以每个影响因素的数值对比率作为变量后验概率验算基础。依据式(4)确定每个变量的后验概率,并根据专家对每个影响因素可能存在发生给出其先验概率,应用式(3)的条件概率进行计算。在问卷调查的专家中具有权威性的专家人数为5人,因此根据表1中给出的模糊语义值表述对问卷调查中这5位专家对影响因素的评价进行整合,给出根节点和中间节点的三角模糊数值矩阵,如下所示:

同理,根据专家对每个变量的观点,如“还行”、“差不多”、“很可能”等模糊词进行三角模糊处理,并利用式(12)、式(13)、式(14)对其进行操作。当η=2时,有如下结果。
利用式(12)对每个变量的在贝叶斯网络中的概率进行三角模糊数均值化处理如下页表3所示。
按照式(13)进行去模糊化操作,实现将概率值精准化,使其变为实数,此时根据专家数可以确定η的取值为3,可得结果如下页表4所示。
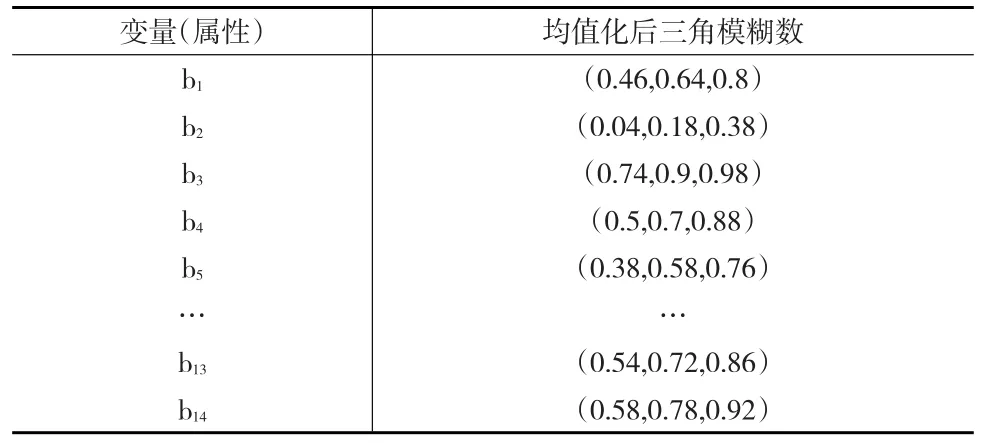
表3 三角模糊数均值化处理结果

表4 三角模糊数去模糊化处理结果
归一化作为一种无量纲处理手段,不仅可以消除无关影响因素,还能进一步精确变量的概率准确度,利用式(3)和式(14)对各根节点和中间节点进行处理,从而得到归一化的处理结果,如表5所示。

表5 无量纲归一化处理结果
2.3 网络舆论危险等级确定
当专家数量M确定为5时,依据式(15)计算各个影响因素的危险指数,计算结果如表6所示。

表6 变量危险指数
根据网络舆情专家系统中给出的危险级别的划分,如表7所示,可以将上述变量进行危险定级。

表7 危险级别划分
根据式(6)的隶属度公式对均值化后的三角模糊数进行操作,确定每个变量属于哪一具体类别,为网络舆论危机等级确定的结果提供类别划分依据,使得分析的结果更具有简单性。
例如,计算变量b1~b5的隶属度,确定其是否属于图1给出的贝叶斯网络结构中的类别,计算结果如表8所示。

表8 变量b1~b5隶属度
当隶属度值大于零时才能说明该变量属于对应的类别,具有的风险类型接近于实际情况,而隶属度值等于零则表明该变量有非常大的可能不属于该类别,或说与该类别的贴近度较低,因此一定程度上加大了该变量转化成危机因素的风险,即在原有风险等级上增加10%的可能度[10]。
3 结束语
本文提出的网络舆论危机识别方法,不仅可以实现对公众舆论的影响因素分析,还能利用贝叶斯网络的概率推理技术对每个影响因素的发生概率及危险化程度进行计算,将定性变量以定量的方式进行表示,从而提高三角模糊数与贝叶斯网络的有效利用率,充分地分析突发事件的网络舆论演化成危机的主体影响因素。为了进一步提高网络危机识别速度,在未来的学术研究工作中将应用分布式处理方式与快速检索算法联合处理,弥补本文在危机识别速度上存在的局限性。
参考文献:
[1]Jensen F V,Nielsen T D.Bayesian Networks and Decision Graphs[J].Springer Berlin,2015,50(3).
[2]相丽玲,王晴.信息公开背景下网络舆情危机演化特征及治理机制研究[J].情报科学,2014,(4).
[3]翟胜,师五喜,修春波.基于模糊贝叶斯网的危害性分析方法[J].计算机应用,2014,34(12).
[4]胡玉胜,涂序彦,崔晓瑜等.基于贝叶斯网络的不确定性知识的推理方法[J].计算机集成制造系统,2001,7(12).
[5]岳超源.决策理论与方法[M].北京:科学出版社,2003.
[6]马宾,殷立峰.一种基于Hadoop平台的并行朴素贝叶斯网络舆情快速分类算法[J].现代图书情报技术,2015,(2).
[7]韩磊,吴树芳,王子贤.贝叶斯网络[J].电脑知识与技术,2009,5(21).
[8]江文奇.基于FVIKOR的三角模糊数型多准则决策方法[J].控制与决策,2016,31(7).
[9]王君,樊治平.知识管理者能力的一种模糊多指标评价方法[J].系统管理学报,2003,12(3).
[10]黄智力,罗键.三角模糊数型不确定多指标决策的可能度关系法[J].控制与决策,2015,30(8).
