保险公司市场风险经济资本度量研究
2018-04-11李秀芳杨雅明
李秀芳, 杨雅明
(南开大学 金融学院,天津 300350)*
一、引言及文献综述
伴随着第二代偿付能力监管要求由规模导向向风险导向的转变,监管资本对风险的度量进行了很大程度的细化。与监管资本相比,经济资本同样是基于各类风险的度量,但其理论体系的构建更强调对于保险公司风险管理的内部性以及对于公司在资本约束、绩效评估、风险管理甚至产品定价等方面的整体适用性[1,2]。近年来,随着保险投资渠道的拓宽以及市场敏感型保险产品的广泛销售,在当前市场背景下,保险公司所面临的市场风险相较于其他各类风险而言是最为突出的。以荷兰国际集团(ING)公司的年度报告为例,在不考虑风险分散化效应的情况下,2012年市场风险经济资本占总经济资本的53.73%,是所有风险分类之中占比最大的风险源。
市场风险的主要考察对象为利率风险和权益类风险。利率模型主要分为两大类:一类是仿射模型,其中具有代表性的有Vasicek[3]模型和CIR[4]模型等,这类模型从具有扩散特性的短期利率出发得到不同期限的利率,刻画利率期限结构的动态变化;另一类是无套利模型,其中具有代表性的如Ho-Lee模型和HJM模型,这类模型从远期利率的扩散过程出发构造利率期限结构模型,其核心是对扩散项的假设。对于权益类风险最常见的建模方法是对证券市场指数的变化过程建模,在实际操作中也可对个股、组合或板块等进行建模。目前常用的股票价格模型有B-S模型[5]、跳跃扩散模型(SVJD)、Garch组模型,以及Regime-Switching类模型等。
由于经济资本是基于大量市场一致性情景对尾部损失进行度量,因此,其最常用的方法是将整体模拟过程分为外部情景和内部情景两部分的嵌套随机模拟方法[6,7],由于嵌套随机模拟涉及多层情景生成,大量的情景生成为实务操作带来了巨大的运算压力,而且保险公司由于投资领域不同,还需要对不同种类投资品进行分类情景生成。Gan和Lin(2015)[8]总结了嵌套随机模拟常见的简化方法,其中包括历史模拟法、资产现金流组合复制法、最小二乘蒙特卡洛法(LSMC)等。其核心思想是通过历史信息找到未来情景从而减少情景路径总数量,或者通过最小二乘方法归纳出几类主要风险驱动因子与资产和负债的关系,并通过对风险因子的生成达到情景生成的简化目的,但这些方法的模型参数与结果校准同样需要大量情景作为支撑。因此,确定合理的情景生成模型和适当的内外部情景生成数量是经济资本度量问题的关键。
目前国内保险行业对于经济资本的引进尚处于初始阶段,保监会2010年颁布的《人身保险公司全面风险管理实施指引》中鼓励“公司应根据自身的业务特质、规模和复杂程度,计量公司潜在的经济价值损失,直观反映公司的风险状况”,并使“经济资本方法成为公司内部使用的核心风险计量工具”,但目前在具体操作与实施规则上并未明确。在我国保险公司经济资本测算理论研究方面,郭祥(2014)对我国非寿险公司基于TVaR测度进行了经济资本测算[9];李秀芳、毕冬(2016)利用Copula函数对财险公司保险风险进行了聚合,并考察了不同业务线间的风险分散化效应[10];邓平紧、李静(2016)基于我国市场状况,利用随机模拟对保险公司利率风险经济资本进行了测算研究[11]。
通过国内外保险公司经济资本度量方面的报告与调研发现,目前经济资本测算主要依托于随机情景生成,为充分发挥经济资本在保险公司的管理作用,为自下而上的总体经济资本测算方法[12,13]提供支持,并使之逐步成为与监管体制下偿付能力资本并行的保险公司内部风险管控工具,本文重点研究运用嵌套随机模拟方法分别在两种风险测度下进行情景生成,并按照我国保险公司资产运用实际比例,结合我国利率、债券及股票的实际状况,对保险公司资产端与负债端市场波动分别进行模拟,并进行市场风险经济资本度量。同时考察测算结果的稳定性与可操作性,并对内外部情景数量的选取进行分析,以期为经济资本方法在我国保险业中的实务操作提供参考。
二、理论模型与参数测算
(一)市场风险经济资本与嵌套随机情景生成
经济资本(EC)是在未来一定时期内,在一定的置信水平下,保险公司为吸收非预期损失而需持有的资本额度。
EC(X)=ρ(X)-E(X)
(1)
在市场风险经济资本的度量中,X为由市场风险引起的损失随机变量,ρ(·)为风险测度,即保险公司可以容忍的总体风险水平,其中包含预期和非预期损失,而经济资本则关注于预期损失之上的非预期损失部分,因此,需要通过风险测度ρ(X)对一定置信水平下的尾分布予以充分度量,实务中比较常用的风险测度有如VAR和TVaR等[13,14]方法。为生成损失情景、度量经济资本,目前最常用的情景生成方法是嵌套随机模拟方法,该方法将模拟分为两个部分:外部情景模拟与内部情景模拟。外部情景模拟,也称为“情景外模拟”,是指基于当前时点资产状况和历史信息在现实世界风险测度下生成的情景,即基于现实情况的情景生成。内部情景模拟,也称为“情景内模拟”,是指在前期生成的外部情景基础上在风险中性世界下生成的经济情景,即基于已生成情景的情景生成。经济情景生成对风险世界的依赖性较大,不同风险世界下情景的用途也不一致。现实世界情景关注投资者的风险偏好,并以历史数据作为条件信息对未来情景进行生成;风险中性世界下所有投资产品的收益率都是无风险利率,同时所选用的模型以及所生成的情景也需要满足风险中性条件。嵌套随机模拟的两个情景生成阶段如图1所示。
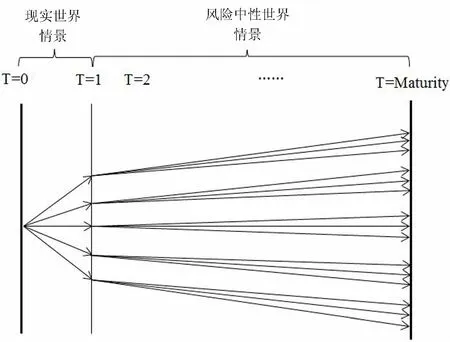
图1 嵌套随机模拟情景生成示意图
(二)基于跳跃模型的利率波动模型
由于我国利率水平受政府政策影响,当前市场化波动效果并不显著,虽然目前刻画利率波动的理论模型较为丰富,但为更客观地描述我国当前阶段利率情况,并在未来产生合理的利率情景,本文在利率模型方面选择泊松跳跃模型对其进行描述[15]。
dit=KtdP
(2)
其中P为服从参数为λ的泊松分布;Kt服从均值为μ,波动率为σit的正态分布。因此,该跳跃模型可理解为以下组合:跳跃满足dit~N(μ,(σit)2)时的概率为λ,而dit=0的概率为1-λ。
对于离散数据的跳跃模型相关参数可用矩估计求得:
(3)
其中n和N分别代表考察期内的利率跳跃次数和样本总量。由于跳跃参数λ和跳跃幅度正态分布之间是独立的,因此可以对两者进行分别估计。本文考察从1999年6月12日至2016年1月31日我国一年定期银行存款利率每周的跳跃情况。样本期间内总周数为816,跳跃次数为26次,因此对λ的估计值为0.0319,由表1可以看出,累积跳跃Gamma分布的估计结果在泊松分布95%置信期间内,可以认为λ的估计是稳定的。
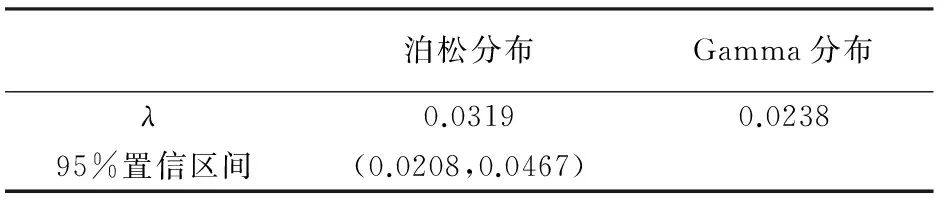
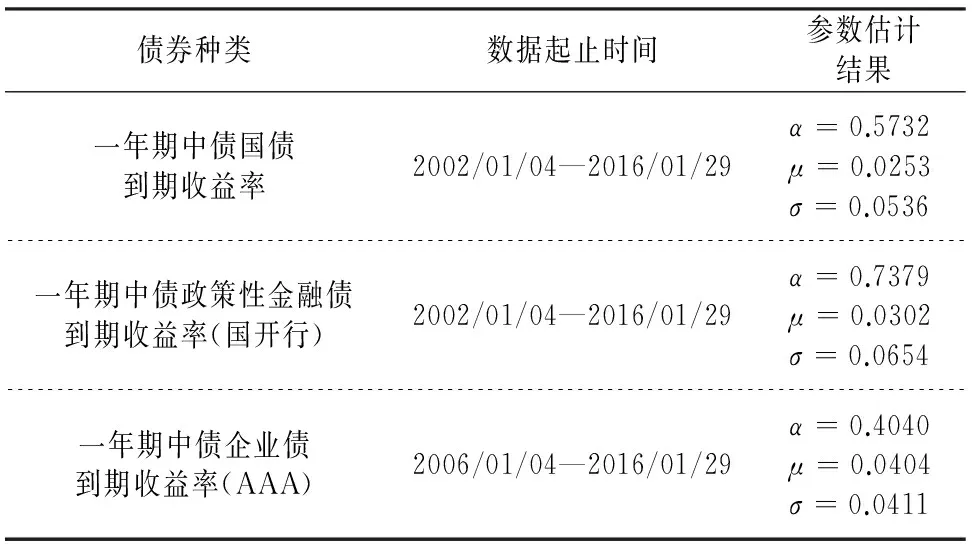
表1 存款利率跳跃次数参数估计
由表2可以看出,我国存款利率整体呈现下调趋势,我国自进入21世纪以来的26次利率调整中,上升与下降的次数相同,但累积的下调幅度大于上升幅度,21世纪初我国一年期定期存款利率为2.25%,自2015年10月24日至考察期末仅为1.5%,所以,对于我国银行存款利率的整体的向下趋势估计结果比较合理。但通过t检验结果发现,该趋势并不满足显著不为0,因此,在接下来估计波动方差时假设跳跃幅度均值为0。

表2 存款利率跳跃幅度参数估计
当存在跳跃情况时,跳跃幅度Kt服从N(0,(σit)2),经过转化可以得到:
dit/it=(Kt/it)dP
(4)
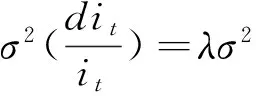
这里采用的利率跳跃模型将跳跃幅度的波动性与当前利率状况相联系,与单纯的跳跃模型相比,模拟过程包含了当前利率状况的条件信息,当利率水平较低时,波动率也相应较小,因此也避免了负利率的生成。
(三)基于CIR模型的债券收益模型
连续型金融波动模型常由趋势项与扩散项两部分组成。由于实际中债券收益常具有均值回复与非负特征,而仿射模型体系下的CIR模型恰好体现了以上两点特征,因此,常被应用于债券类收益率情景模拟。CIR模型形式如下:
(5)
其中α和μ分别是收益率回复的速度与均值。CIR模型条件概率分布服从非中心χ2分布:
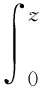
(6)
其中υ和λ分别表示非中心χ2分布的自由度以及非中心化平移参数。
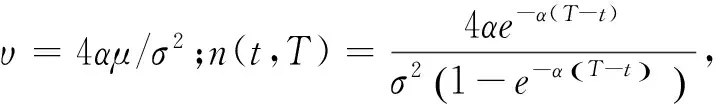
T>t,则给定x(t)时,x(T)的分布为伸缩e-α(T-t)/n(T-t)倍的、自由度为υ、非中心化参数为λ=x(t)·n(t,T)的χ2分布,即:
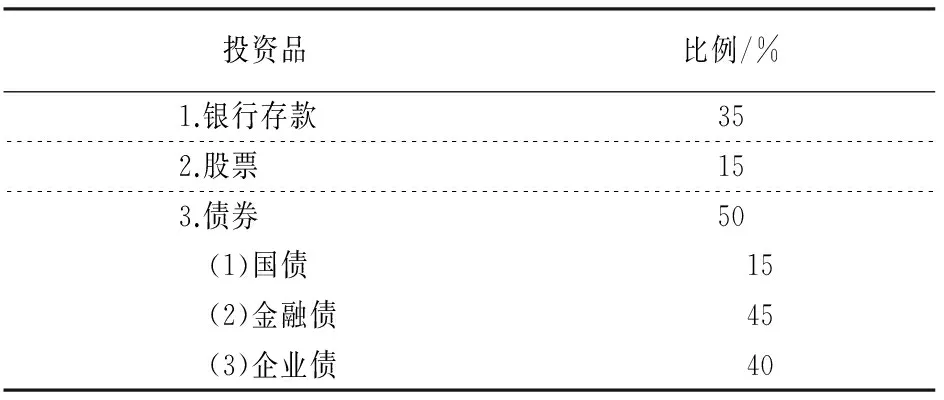
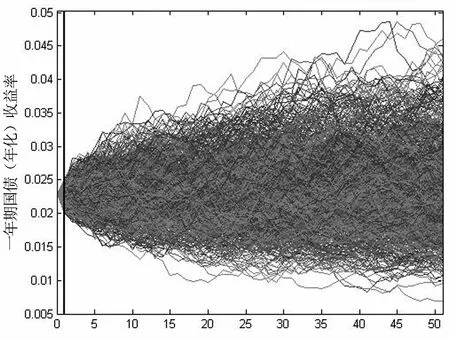
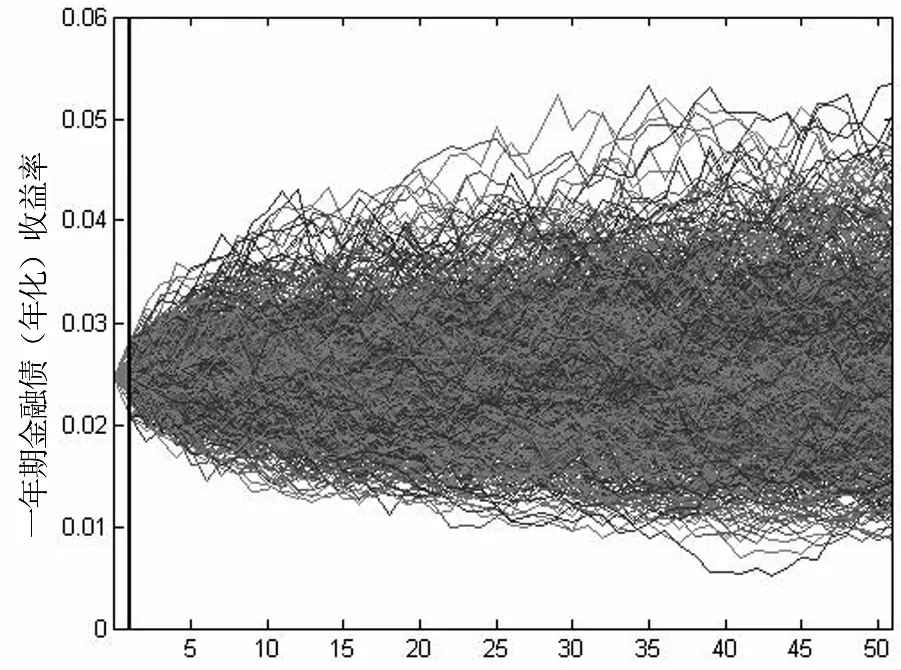
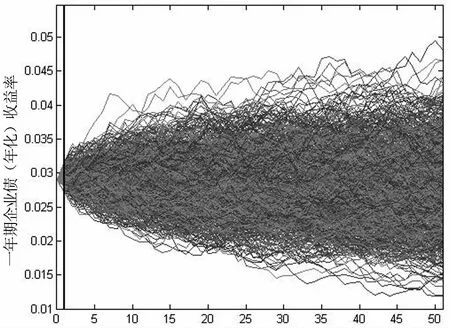
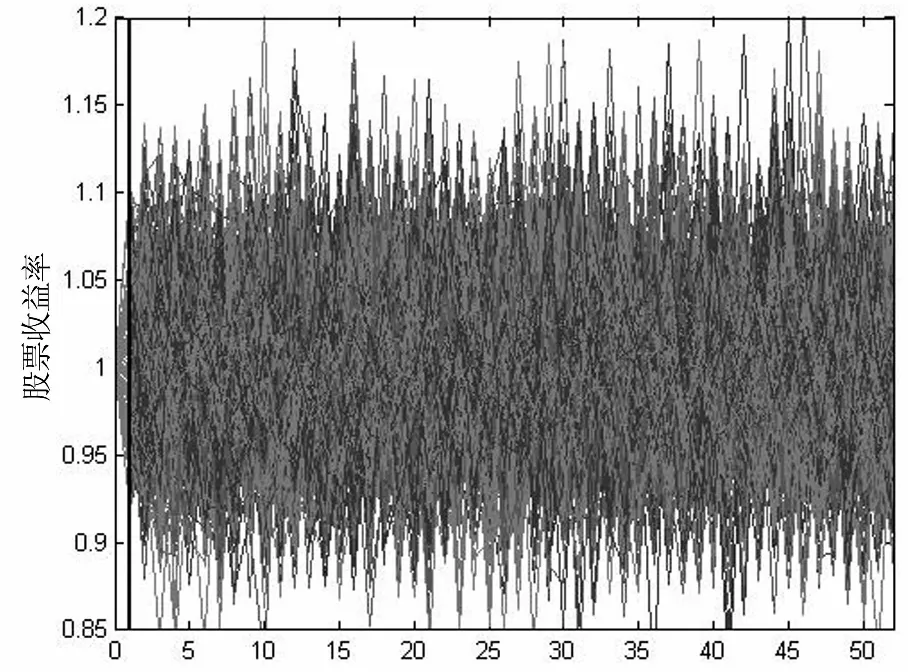
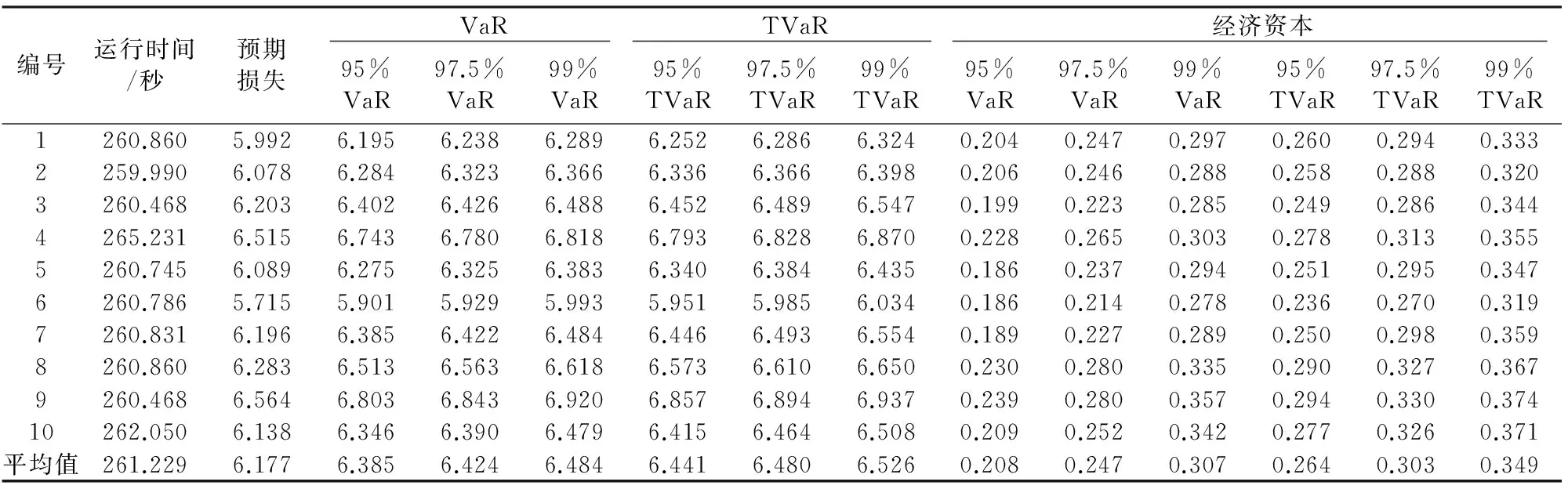
Pr (x(T) (7) 模型参数集元素可通过最大化似然函数求得: (8) 根据公开可获取的数据,首先分别对我国一年期国债、金融债和企业债收益率数据进行周平滑处理,然后通过极大似然估计方法进行CIR模型周数据的参数估计,结果如表3所示。在后面的实证研究部分将采用该参数估计结果并运用Euler方法进行债券收益率的外部情景生成[16]。 表3 我国债券收益率CIR模型参数估计 数据来源:wind数据库。 制度转换模型是指模型参数在不同制度体系下,可以分别取不同值的时间序列模型。常见的制度转换包括两大类:阈值模型与马尔可夫转换模型。阈值模型的制度间转换触发因素是可观察变量的值达到了模型的阈值,进而发生制度间转换[17];马尔可夫转换模型的转换规则遵循马尔可夫过程。本文在权益类资产波动模拟过程中选取刻画较长时间间隔波动数据的对数正态体制转换模型用于股票情景模拟[18]。 传统的包括Black-Sholes方法在内的股票价格模型假设价格波动服从几何布朗运动,在任意离散时间间隔下,股票收益率服从对数正态分布,即独立对数正态模型(Independent Lognormal Model, ILM)。 (9) 该模型形式简单,对高频波动收益率数据较为适用,但对于较长时间间隔数据的适用性较差,因此,选用制度转换对数正态模型,以便更好地拟合股票波动。在该模型下,假设股票收益在某一时间间隔内处于体制K内,其波动服从该体制参数体系下的对数正态分布形式,不同体制间存在一个马尔可夫转移概率矩阵,在情景路径的生成过程中,每一步新的情景都有留在该体制内与转移到另外体制下的概率。 用ρt表示在时间间隔[t,t+1)内收益率所处的状态,t时刻股价指数服从以下对数正态过程: (10) 状态转移矩阵为P,其中pij表示由状态i转移到状态j的概率。 pij=Pr [ρt+1=j|ρt=i] i=1,2;j=1,2 考虑到模型参数个数问题,在建模过程中选取双体制制度转换模型,即ρt=1,2,因此,模型中的待估参数集为Θ={μ1,μ2,σ1,σ2,p1,2,p2,1}。 在情景生成过程中首先将马尔可夫稳定状态下两个状态的概率作为迭代起始,进行逐步迭代,最终通过最大化似然函数之和求出六个待估参数值。通过对我国上证综指2000年1月到2016年1月周数据作为样本进行实证分析,利用MATLAB迭代求解可以得出RSLN模型参数,结果如表4所示。 表4 RSLN股票价格模型参数估计(周) 通过表4可以看出,上证综指周收益率变化的两个体制中有一个具有较高波动性的正均值收益率状态与一个具有较低波动性的负均值收益率(接近于0)的状态,两状态间的相互转移概率较低,即状态间转移频率较小。 假设保险公司的资金用以下三类方式进行投资:银行存款、债券类产品及股票,利用保监会公布的保险统计数据对我国2013-2015年保险资金运用余额进行分析,可以将投资资产按照表5所示的比例进行配置。其中债券类投资品又可以进一步细分类为国债、金融债及企业债三类。 表5 保险公司资产端投资品比例 首先,对于每种投资品在现实世界风险测度下生成第一期的100个外部情景;然后,针对每一个外部情景在风险中性世界测度下生成10条内部情景,由此外部情景与内部情景构成共100×10条路径。情景生成模型分别利用利率跳跃模型、债券收益率CIR模型以及股票制度转换RSLN模型,其中外部情景利用历史数据估计模型参数,内部情景生成部分选取我国一年期国债收益率作为无风险收益率的代表进行情景生成。由于RSLN模型在风险中性测度下参数不是唯一的,故采用Q测度下的参数确定方法[19]确定股票内部情景模拟的两状态收益率波动均值,并保持两状态波动标准差与马尔可夫转移概率不变。此外,考虑到现实中股票与债券收益波动具有显著的相关性,因此,股票收益率内外部情景生成过程中,采用Cholesky分解对股票和债券进行成组生成[20]。 假设保险公司包含市场风险敏感型产品与非敏感型两类。对于市场风险敏感型产品的测算,假设在经济资本测算起始时点,保险公司拥有100份投资连结型保单,各项保单特征如表6所示,保险事故发生后,保险金额为事故发生时刻账户价值,投资连结产品账户所包含的投资品组合仍假设为由银行存款、债券类和股票构成,情景路径生成方法与资产端路径生成方法一致。同时保留5%的现金资产,资产配置如表7所示。对于非市场敏感型产品,假设在经济资本测算时点,保险公司拥有500份终身寿险保单,保单特征如表6所示。 表6 保险公司两种类型保单特征表 表7 投资连结型保单账户资产构成表 首先,分类别生成投资品嵌套随机情景路径。图2~5分别列示了国债、金融债、企业债以及股票的两阶段嵌套情景路径,其中第一期为100组外部情景,后期为100×10组内部情景。 周 steps 然后,根据投资品路径分别生成资产情景与负债情景。资产端在期初按照单位资产进行计算,并按照表5所示的比例投资,生成单位资产在一年内的情景路径。负债端两种类型保单按照表6和表7的保单特征分别进行随机生成,市场敏感型保单根据各类投资比例按照第一步的路径进行组合。为准确度量市场风险经济资本,剔除死亡率波动所带来的非预期损失,投保人生存概率按照2000-2003年版生命表计算,各年龄段死亡率在年内服从均匀分布。 steps 周 最后,在上述生成的资产端与负债端情景路径下,计算各置信水平下的损失额,并用相应风险测度的损失减去预期损失,即EC=ρ(X)-E(X),便可得到市场风险经济资本。接下来多次重复以上流程观察计算结果稳定性。 表8显示了多次情景模拟下保险公司损失的VaR、TVaR值以及市场风险经济资本数额。 表8 保险公司市场风险经济资本预测结果(100×10) 单位:10万元 从表8中的十次模拟结果来看,受模拟情景的随机性影响,不同置信水平下多次模拟所需资本的VaR和TVaR略有差异,但市场风险经济资本预测结果大致稳定,运行时间约在260秒左右。实务中适合对本模型进行多次操作,操作中可以适当增加情景模拟路径数量或根据保险公司自身风险特点调整度量模型以及投资品组合品种及配置比例;同时公司对于风险度量标准的选取对于实际市场风险经济资本数额的确定也具有重大影响,公司应根据自身风险偏好及风险容忍程度酌情选取。 通过表9和表10可以看出,当模拟次数较少时,对于非预期损失常常估计不足且不同次模拟之间结果差异显著。随着内部情景和外部情景数量的分别增加,模拟结果对于极端情景下的经济资本预测更为充分,多次模拟结果随机性减小,结果趋于一致(括号中数值为10次模拟的标准差)。当模拟情景数量增加时,受硬件条件限制,每次运行时间较长,公司在实务中应综合考虑情景生成的精确性与时间成本。 Gan和Lin(2015)[8]指出嵌套随机模拟的内外部情景作用不尽相同,外部情景着重对损失分布的产生,内部情景则是基于外部情景的条件期望,可用于金融产品的定价。外部情景不足会产生结果的有偏估计,内部情景生成数量减少则会造成度量结果波动性过大,因此,保险公司应根据实际需求确定内外部模拟数量。在本例的模拟结果中,当内部与外部情景数量乘积一定的情况下,无论内外部情景数量如何分配,模拟时间基本相同,但实际的市场风险经济资本预测结果会受现实世界与风险中性世界之间风险溢价影响而造成模型参数差异,导致模拟效果不同。如果参数差异较小,则在内外部情景数量乘积数量一定的情况下,内外部情景各自的数量配置对市场风险经济资本的测算影响并不明显,此时公司在测算结果稳定的前提下可以适量同时减少内、外部情景生成数量;如果参数差异较大,则内外部情景数量配置的区别会造成模拟结果较大的差异,此时一般应考虑对内、外部情景都进行充分的模拟。 表9 保险公司市场风险经济资本预测结果(内部情景数为10) 单位:10万元 表10 保险公司市场风险经济资本预测结果(外部情景数为100) 单位:10万元 本文分别对资产和负债端建立模型并考虑银行存款、债券类及股票投资,采用嵌套随机模拟方法,在不同情景数量下进行市场风险经济资本测算。当模拟路径数量增加到一定程度时,对于极端情景的模拟趋于稳定,内部与外部情景生成的数量乘积一定时,运算时间基本一致;内、外两阶段情景的参数差异较小时,可适当减少模拟次数,但当参数差异较大时,应保证充足的内、外部模拟的次数。保险公司在实际操作中应综合考虑模拟精确性与运算时间成本。 考虑到寿险产品保单的长期性,本文对市场风险经济资本的度量仅以寿险业务为例,相对而言非寿险业务由于保单期限短,市场风险影响不如寿险业务明显,但并不表示市场风险对非寿险业务没有影响,对于非寿险业务的经济资本建模也将是今后的一个研究方向。在度量方法方面,积极探索基于宏观经济指标视角下市场风险经济资本的测算方法也是未来的一个研究方向,该方向研究重心将转移至对宏观经济波动及其与经济资本度量的联系上而非仅限于投资品的自身历史波动状况。度量技术层面,由于情景生成在实务操作中是一个重要环节,当情景较多时,运算成本消耗较高,因此,对于情景生成的简化方法一直是经济资本研究理论的一大热点,例如在嵌套随机模拟中,最小二乘蒙特卡洛方法的运用将显著降低对于风险中性情景数量的要求,但风险驱动因子的选取以及回归形式的确定是该问题的难点,因此,在该方面的研究也是十分有意义的。 参考文献: [1]魏迎宁, 陈戈. 论保险公司经济资本[J]. 保险研究, 2008(5):64-66. [2]杨卫平, 周咪, 成萌. 互联网金融背景下中国寿险公司经营绩效评价研究[J]. 财经理论与实践, 2016, 37(4):31-36. [3]Vasicek O. An equilibrium characterization of the term structure[J]. Journal of financial economics, 1977, 5(2): 177-188. [4]Cox J C, Ingersoll Jr J E, Ross S A. A theory of the term structure of interest rates[J]. Econometrica: Journal of the Econometric Society, 1985,53(2): 385-407. [5]Black F, Scholes M. The pricing of options and corporate liabilities[J]. The Journal of Political Economy, 1973,81(3): 637-654. [6]Bauer D, Reuss A, Singer D. On the calculation of the solvency capital requirement based on nested simulations[J]. Astin Bulletin, 2012, 42(02): 453-499. [7]Reynolds C, Man S. Nested stochastic pricing:the time Has come. product matters[J]. Society of Actuaries, 2008, 71: 16-20. [8]Gan G, Lin X S. Valuation of large variable annuity portfolios under nested simulation:a functional data approach[J]. Insurance: Mathematics and Economics, 2015, 62: 138-150. [9]郭祥. 我国保险公司经济资本管理研究[D].北京:对外经济贸易大学, 2014. [10] 李秀芳, 毕冬.基于Copula函数的财险公司风险聚合和经济资本分散化效用研究[J]. 保险研究, 2016(6):48 -60. [11] 邓平紧, 李静. “偿二代”框架下情景生成对利率风险经济资本的影响[J]. 保险研究, 2016(9):41-47. [12] 杨继光, 刘海龙. 基于期权的商业银行总体经济资本测度研究[A]/第十届中国管理 科学学术年会论文集[C]. 2008:255-258. [13] Klaassen P, van Eeghen I. Economic capital: how it works, and what every manager needs to know[M]. Elsevier, 2009. [14] 王稳, 郭祥. 基于TailVaR的我国保险公司经济资本度量研究[J]. 中国软科学, 2012(5):148-156. [15] 林海, 郑振龙. 中国利率动态模型研究[J]. 财经问题研究, 2005(9):45-49. [16] Kladivko K. Maximum likelihood estimation of the Cox-Ingersoll-Ross process: the matlab implementation[J]. Technical Computing Prague, 2007. [17] Piger J. Econometrics: models of regime changes[A].Complex Systems in Finance and Econometrics[C]. Springer New York, 2009: 190-202. [18] Hardy M R. A regime-switching model of long-term stock returns[J]. North American Actuarial Journal, 2001, 5(2): 41-53. [19] Bollen N P B. Valuing options in regime-switching models[J]. The Journal of Derivatives, 1998, 6(1): 38-49. [20] Zhu N, Bauer D. Applications of forward mortality factor models in life insurance practice[J]. The Geneva Papers on Risk and Insurance-Issues and Practice, 2011, 36(4): 567-594.
(四)基于制度转换模型(RSLN)的股票价格模型

三、数值模拟与讨论
(一)资产端情景生成
(二)负债端情景生成


(三)市场风险经济资本测算
(四)测算结果分析


四、结论与展望
