两通道正交图滤波器组设计新算法

蒋俊正， 曹　想， 欧阳缮

(桂林电子科技大学 信息与通信学院, 广西 桂林 541004)

图作为一种有效的建模工具，可用于刻画非规则网络上的数据，例如社交网络、计算机科学网络和分子生物学网络[1-4]等复杂网络的数据．基于图频谱理论构建的图信号处理，可用于分析和处理非规则定义的网络数据信号，从而克服传统信号处理方法不适用于非规则信号的缺点．在图信号处理的理论框架中，图傅里叶变换是全局变换，不适用于处理大规模的网络数据．为了克服这方面的不足，有许多文献提出了适用于图信号处理的小波变换[5-7].例如，适用于交通网络图的类小波变换[5]，基于图频谱理论构造的任意的有限加权图小波变换[6]，以“扩散小波”为特征空间的基函数[7]．然而，这些小波变换不是临界采样的，不适用于许多信号处理应用，如信号压缩．为了弥补这一缺陷，文献[8]构造了两通道正交图滤波器组，其具备临界采样特性．并提出了基于切比雪夫多项式的近似Meyer核函数设计方法，但是滤波器组重构特性较差，设计中也没有考虑图滤波器的频率特性．文献[9]提出了基于伯恩斯坦多项式逼近的方法，将两通道正交图滤波器组的设计问题归结为带约束的优化问题，设计所得的图滤波器组整体性能良好．在图滤波器组的研究工作中，两通道图滤波器组具备临界采样和(近似)完全重构等优点．目前，两通道图滤波器组的研究相对较少，更为有效的设计算法有待提出.

笔者考虑两通道正交图滤波器组的设计问题，根据图滤波器组的性能指标，将设计问题归结为一个带约束的优化问题．由于目标函数是关于图滤波器系数的四次函数，优化问题难于求解．为此，通过泰勒近似将高度非线性非凸的目标函数近似转化为凸二次函数，从而，将非凸优化问题近似为凸的优化问题．进而，采用迭代方法求解得到图滤波器系数．与文献[8-9]给出的方法进行仿真对比发现，所提出的新算法设计的两通道正交图滤波器组重构误差更小，信噪比更大，滤波器的频率特性良好．

1　两通道正交图滤波器组的结构

图1给出了两通道正交图滤波器组的结构，其中，βH为采样因子，H0和H1构成了分析滤波器组，G0和G1构成了综合滤波器组．在两通道正交图滤波器组里，4个子带滤波器H0、H1、G0和G1由1个滤波器h0(λ)决定[8]，可表示为

(1)

两通道正交图滤波器组的输入输出关系为

(2)

(3)

其中，x=λ-1，表示平移的频率．

(4)

(5)

(6)

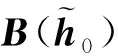
2　两通道正交图滤波器组的设计

2.1　图滤波器组的性能指标

两通道正交图滤波器组的设计包含了许多性能指标: 重构误差、滤波器的通带平坦性和阻带衰减．重构误差衡量滤波器组的重构特性，通带平坦性和阻带衰减衡量滤波器的频率特性[11]．一般来说，重构误差和阻带衰减可用于控制图滤波器组的整体性能．

两通道正交图滤波器组在xi点的重构误差可表示为

其中，xi(i=0，1, …，K-1)表示为区间[0，1]上的均匀离散点．

另外，滤波器的阻带衰减通过阻带波纹来控制，给定很小的δs，阻带波纹限定为

(9)

2.2　滤波器的设计

基于前面的分析，可以将两通道正交图滤波器组的设计问题归结为如下的带约束优化问题:

(10)

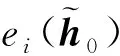
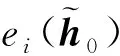
矩阵U(·)可以认为是一个操作，将2L-1维的列向量转换为一个L×L的矩阵[10]．

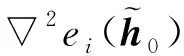
(13)

(14)

(15)

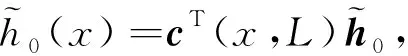
(16)

3　仿真结果与分析

将给出文中算法与文献[8-9]的算法进行仿真对比．所有的仿真和对比都是在相同环境下运行的．两通道正交图滤波器组的性能指标包括:

(2) 信噪比．性能指标计算方法与文献[9]的相同．为了确保设计精度，离散点的数量在区间[0，1]取K+1= 101．在问题(P2)中，区间[xs，1]离散点数量是 (K+ 1)(1-xs)．

设计一个两通道正交图滤波器组，子带滤波器的长度L=11，为了与文献[9]的方法公平比较，设阻带截止频率xs= 0.6，其他相关参数xp= -0.3，δs= 0.15．文中算法进行了29次迭代，得到的滤波器系数见表1．文中算法与文献[8-9]设计的图滤波器对比如图2所示．表2给出了文献[8-9]的方法和文中算法的性能比较结果．可以看出，文中算法设计得到的两通道正交图滤波器组具有更小的重构误差，信噪比更大，可以更好地恢复原信号．同时，文中将阻带衰减作为优化的性能指标，设计所得的滤波器具有较好的频率特性．

表1　文中算法设计所得的滤波器系数

表2　文中算法与文献[8-9]算法的性能对比

图2 文献[8-9]算法与文中算法设计所得的低通原型图滤波器图3 明尼苏达交通网络的分解图

最后，将文中算法设计的正交图滤波器组用于分解明尼苏达交通网络信号，分解的结果如图3所示．其中HL通道的子带系数全为零，原因是本图是3着色的．图3表明，LL子带信号表示原始信号的近似，LH和HH两个子带包含图信号的细节信息．重构信号的信噪比为 89.60 dB， 明显大于文献[9]的信噪比 80.99 dB．另外，从表2可以看出，文献[8]的算法设计的图滤波器组的重构误差和信噪比都较差，不适用于实际网络数据的处理．

4　结 束 语

文中围绕两通道正交图滤波器组的设计问题，提出了基于泰勒近似的迭代设计算法．在该算法中，两通道正交图滤波器组的设计问题被归结为一个带约束优化问题，目标函数是图滤波器组的重构误差，约束函数是滤波器的阻带衰减．采用泰勒近似简化目标函数，利用迭代算法有效地求解了设计问题．仿真结果表明，新算法设计的两通道正交图滤波器组的整体性能优于现有算法．另外，文中算法可以扩展到设计过采样图滤波器组．

参考文献：

[1] DUNN S, WILKINSON S M. Increasing the Resilience of Air Traffic Networks Using a Network Graph Theory Approach[J]. Transportation Research Part E: Logistics and Transportation Review, 2016, 90: 39-50.

[2]YOON W, HYUN E. Economic, Social and Institutional Conditions of Network Governance: Network Governance in East Asia[J]. Management Decision, 2010, 48(8): 1212-1229.

[3]ARLEO A, DIDIMO W, LIOTTA G, et al. Large Graph Visualizations Using a Distributed Computing Platform[J]. Information Sciences, 2017, 381: 124-141.

[4]COREL E, LOPEZ P, MÉHEUST R, et al. Network-Thinking: Graphs to Analyze Microbial Complexity and Evolution[J]. Trends in Microbiology, 2016, 24(3): 224-237.

[5]CROVELLA M, KOLACZYK E. Graph Wavelets for Spatial Traffic Analysis[C]//Proceedings of Joint Conference of the 2003 IEEE Computer and Communications: 3. Piscataway: IEEE, 2003: 1848-1857.

[6]HAMMOND D K, VANDERGHEYNST P, GRIBONVAL R. Wavelets on Graphs via Spectral Graph Theory[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 129-150.

[7]COIFMAN R R, MAGGIONI M. Diffusion Wavelets[J]. Applied and Computational Harmonic Analysis, 2006, 21(1): 53-94.

[8]NARANG S K, ORTEGA A. Perfect Reconstruction Two-channel Wavelet Filter Banks for Graph Structured Data[J]. IEEE Transactions on Signal Processing, 2012, 60(6): 2786-2799.

[9]TAY D B H, LIN Z. Design of Near Orthogonal Graph Filter Banks[J]. IEEE Signal Processing Letters, 2015, 22(6): 701-704.

[10]JIANG J Z, SHUI P L, ZHANG Z J. Design of Oversampled DFT-modulated Filter Banks via Modified Newton’s Method[J]. IET Signal Processing, 2011, 5(3): 271-280.

[11]蒋俊正, 王小龙, 水鹏朗. 一种设计DFT调制滤波器组的新算法[J]. 西安电子科技大学学报, 2010, 37(4): 689-693.

JIANG Junzheng, WANG Xiaolong, SHUI Penglang. Novel Method for Designing DFT Modulated Filter Banks[J]. Journal of Xidian University, 2010, 37(4): 689-693.

[12]JIANG J Z, ZHOU F, SHUI P L. Optimization Design of Two-channel Biorthogonal Graph Filter Banks[J]. Circuits, Systems, and Signal Processing, 2016, 35(2): 685-692.