神奇的“变形术”
2018-04-10□倪艳
□倪 艳
“身穿金甲光闪闪,头戴金冠亮晶晶。手举金箍棒一根,足踏云鞋皆相称。一双怪眼似明星,声音响亮如钟磬。尖嘴龇牙弼马温,心高要做齐天圣。”大家知道这首诗描写的是谁吗?对了,他就是大名鼎鼎的孙悟空。孙悟空的神通广大,源自他善于“七十二变”。那孙悟空的“变形术”能解决数学上的问题吗?小朋友,下面我们就来看看悟空在计算王国中,如何用“变形术”神机妙算。

例1.计算99998+9998+998+98+8。
我是这样解的。
先给5个加数都添上2,让它们分别变形为10万、1万、1千、1百和1十,求出它们的和后,再减去添上的5个2。也可以先将算式中的8变形为4个2,再将每个2与前面的加数分别结合,使其分别变形为10万、1万、1千和1百。
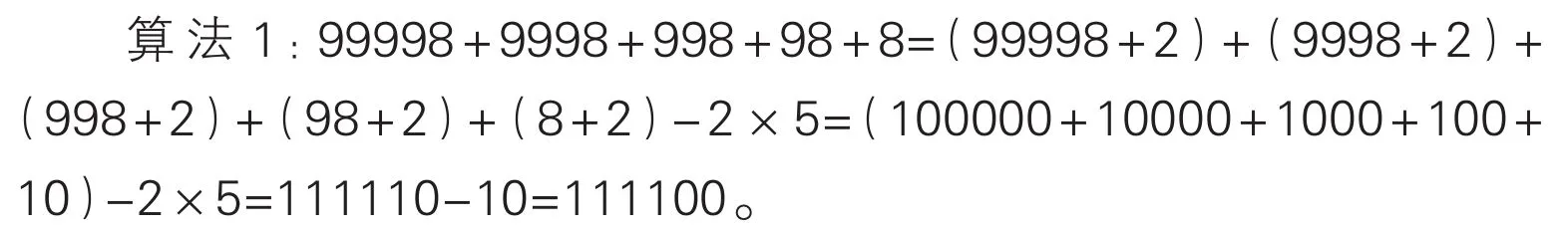

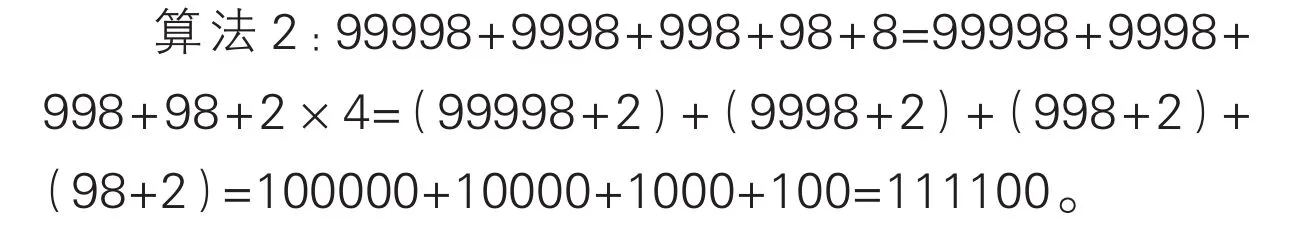
例2.计算2035-568-235-432。
我是这样解的。
先将算式中第二个减数的位置前移,成为第一个减数,以便被减数去尾变形;原式中第一个和第三个减数可以凑成整千数,所以可根据减法的性质减去这两个减数的和。

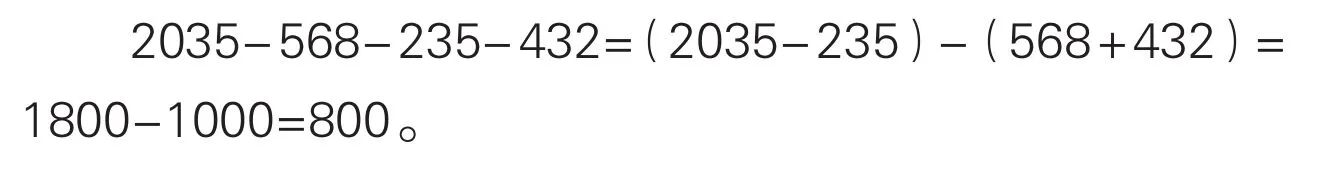
例3.你知道125×25×64积的末尾有几个0吗?
我是这样解的。
可以通过计算得出答案。算式中有因数125和25,只要给它们分别配上因数8和4,计算起来就非常简便。所以将64变形为8×4×2,问题就会迎刃而解。

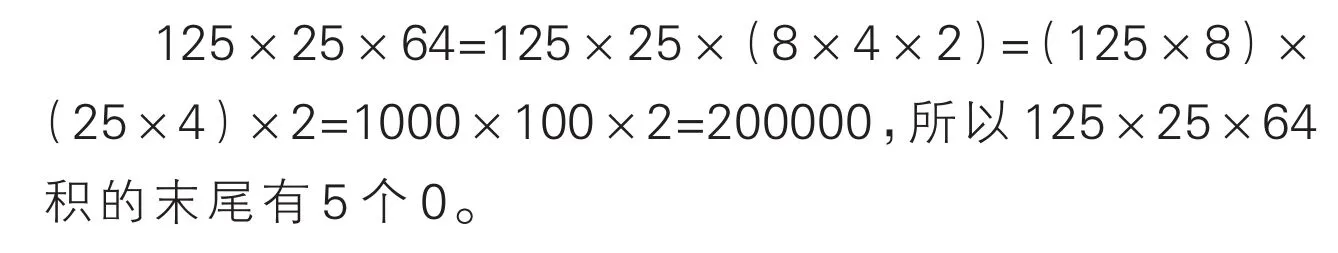
例4.计算:10000÷16÷5÷125。
我是这样解的。
先根据“一个数除以几个数,等于这个数除以这几个数的积”,将算式变形为10000÷(16×5×125);再根据2×5=10和8×125=1000,将除数中的16变形为2×8,这样利用乘法交换律和结合律就能巧算出除数,接着算出商。


例5.计算:6666×2222+4444×6667。
我是这样解的。
根据算式中2222的2倍是4444,先把6666×2222变形为3333×4444,或者把4444×6667变形为2222×13334,接着就可以利用乘法分配律进行简算了。



例6.不计算,你能比较20182018×2019的积与20192019×2018的积的大小吗?
我是这样解的。
算式中的两个因数20182018和20192019都有共同的特点,即前四位上的数字与后四位上的数字相同,因此,可以将20182018变形为20182018=20180000+2018=2018×10000+2018=2018×(10000+1)=2018×10001。同样,20192019=2019×10000+2019=2019×(10000+1)=2019×10001。这样20182018×2019=2018×10001×2019,20192019×2018=2019×10001×2018,可见两个算式中所含的三个因数都相同,因而它们的积相等。

小朋友,只要你细心观察,并根据题中数据的特点,将算式合理变形,你一定能发现算式中隐藏的规律,并从中享受计算的乐趣。
让我们的思维在“变形术”中越变越灵活吧!
