TI介质带限射线束传播及偏移方法

韩冰凯　顾汉明*　刘少勇

(①中国地质大学地球物理与空间信息学院，湖北武汉 430074； ②地球内部多尺度成像湖北省重点实验室，湖北武汉 430074)

1　引言

经典射线(束)传播算子在地震波偏移成像中应用广泛，其高频近似假设的成立条件是介质在第一菲涅耳带内足够光滑[1]，导致射线类传播算子在复杂介质中的应用受到限制。基于双程波波动方程的逆时偏移，能够准确描述复杂介质中带限波场的传播，但计算效率偏低，且输出角度域共成像点道集需要额外计算量[2,3]。在射线理论框架下，发展更准确地传播带限地震波场的传播算子进行偏移成像和速度分析，有重要的理论意义和应用潜力。

Foreman[4]推导了与频率相关的射线追踪系统，相比于传统的射线追踪系统，其计算复杂度显著增加。Protasov等[5]分析了与频率相关的射线追踪系统的算法结构，并与传统射线追踪、时间域有限差分求解波动方程的波场进行了对比，结果表明对应震源子波频带特征的带限射线能够改善射线阴影区成像。Biondi[6]从波动方程出发，推导出与频率相关的程函方程，通过构建非线性偏微分方程求解与频率相关的程函方程，但其低频部分的求解过程需利用已计算的高频部分的结果，需额外的计算量。Lomax[7]通过对垂直于射线平面波长范围内的速度场平滑，以加权平均的速度进行射线追踪。Zelt等[8]在有限差分求解程函方程过程中，对差分节点的速度用波长范围内的加权平均速度代替，并指出该平滑过程等价于波长范围内的速度预平滑，在不改变传统有限差分求解程函方程的前提下高效计算有限频旅行时场，并发展了基于该速度预平滑算子的有限频层析反演算法。Chen等[9]通过与有限差分波动方程正演模拟的波场和波形记录对比，分析了波长内速度平滑算子对有限频旅行时场的影响。Protasov等[10]提出一种与频率有关的射线追踪算法，指出带限射线通过速度界面时，其方向对应第一菲涅耳带内地震波场传播的最大能量方向，即带限射线的传播遵循带限Snell定律。Yarman等[11]从Kirchhoff边界积分出发，推导了带限Snell定律的表达式，并将带限射线追踪应用于Kirchhoff积分偏移中。Yarman等的算法不需要对速度模型进行平滑，但需要已知明确的速度界面信息，这在一定程度上限制了此方法的应用。刘少勇等[12]基于带限射线追踪构建了各向同性介质的带限局部平面波传播算子，并应用于射线束偏移。

地下介质的各向异性普遍存在，且介质各向异性对成像聚焦和成像点位置的影响不容忽略[13]。随着油气勘探技术的发展，在地震资料处理过程中考虑各向异性效应已经逐渐从前沿技术探索转变成为常规处理流程。基于不同的各向异性地震波传播算子，可以发展出不同的各向异性介质成像算法。基于双程波方程的逆时偏移技术可以扩展到适应横各向同性(TI)介质[14,15]，但是其计算效率低。通过引入TI介质射线追踪[16,17]或适用于TI介质的波前类旅行时计算方法，如动态规划法[18]和有限差分求解程函方程法[19,20]，Kirchhoff积分叠前深度偏移可以方便地推广到TI介质[21,22]。经典的高斯束成像[23-26]也可以方便地扩展到TI介质中[27-29]。各向异性介质中射线类偏移算法同样也受限于高频近似假设，存在射线照明的阴影区和焦散现象等[30]。本文基于TI介质射线追踪系统，在局部平面波近似下构建TI介质带限射线追踪算法；结合旁轴近似，基于带限中心射线构建带限射线束传播算子，并应用于TI介质的射线束偏移。

2　方法原理

2.1　带限射线追踪

基于高频近似的射线追踪是假设地震波的能量沿宽度为零的射线传播，高频射线也称作费马射线。带限射线理论描述地震波能量沿有宽度的波路径传播，为一类胖射线[31]。如图1所示，对于波长尺度的速度异常体(图1a)，波传播路径(红色箭头)受到影响，而经过异常体附近的高频射线路径(黑色箭头)并没有改变；对于远小于一个波长的速度异常体(图1b)，波传播路径没有发生明显改变，但高频射线路径发生明显偏转[7]。因此，高频射线难以准确描述带限波场传播的特征。

从声波波动方程出发，含震源介质透过界面Γ的透射波场[32]表达为

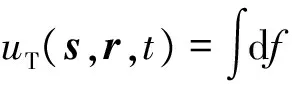
uI(s,x,f)∂nG2(x,r,f)]T(x)e-2πftdsΓ(x)

(1)

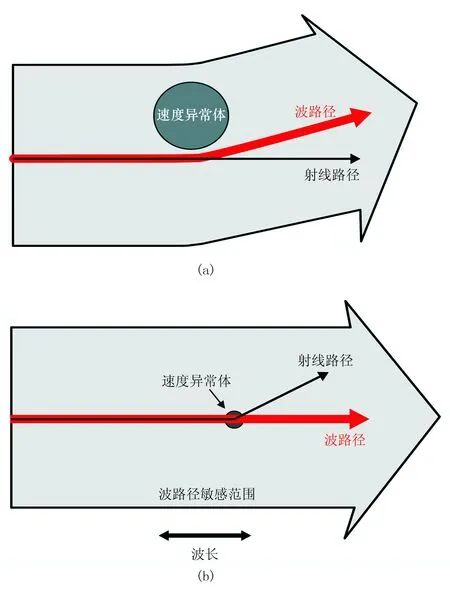
图1　高频射线与带限波路径对比示意图[7]

uT(s,r,t)≈4∬Γ{A(x,s,r)T(x)cos(2πfc[τ(x,s,r)-

t] sinc(2πfb[τ(x,s,r)-t])}dsΓ(x)

(2)

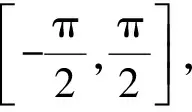
(3)

对于带宽为B的带限震源，在x0附近，限定第一菲涅耳带内的Kirchhoff积分由u(s,r,x0)=uT[s,r,τ(x0,s,r)]给出[11]，即

sinc(2πB[Δτ(x,x0,s,r)])dsΓ(x)

(4)

式中： FZx0表示x0附近由式(3)限定的第一菲涅耳带； Δτ(x,x0,s,r)=τ(x,s,r)-τ(x0,s,r)。带限Snell定律定义为使式(4)中透射波场u(s,r,x0)振幅取得最大值的波传播方向，即x0处第一菲涅耳带FZx0内射线入射方向p1(x)和出射方向p2(x)满足如下关系式

(5)

式中 ‖p2‖2=1。在局部平面波的假设下，若A(x,s,r)和T(x)为常数，对于界面上的任意一点x∈FZx0，当p2(x0)满足下式时，式(4)有最大值

(6)

式中v1和v2分别表示界面两侧的速度。式(6)的物理含义为，在第一菲涅耳带FZx0内，存在等效的局部平面波，能够描述式(4)表征的穿过界面Γ的带限透射波场，透射波场的传播方向p2对应频带B的带限波场传播的最大能量方向。由式(5)表征的带限Snell定律控制带限射线追踪系统，带限射线传播可由式(6)表达的等效局部平面波实现。

2.2　TI介质带限射线束传播与偏移

在各向异性介质中，以Thomsen各向异性参数表征的qP波相速度是相角的函数[33]。Alkhalifa[17]通过qS波垂直各向同性面的相速度为零的假设，得到TI介质的各向异性相速度表达式。Jiang等[34]分析了qP波相速度对弹性刚度系数C13的敏感性，在|δ|≪1的假设下，对C13以线性近似推导出VTI介质近似qP波相速度公式

(7)

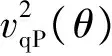
(8)

上述射线控制方程可用于描述TI介质中局部平面波的传播。如图2a所示，在x0处第一菲涅耳带FZx0内构建局部平面波，以灰色矩形表示的局部平面波由一定密度且方向相同的各向异性高频射线构成，对应射线参数(pin,pout)的单条射线，在x∈Γx0的传播遵循式(8)。进一步，由透射射线参数pout加权得到等效射线参数p2。数学上，该过程对应惩罚区间为第一菲涅耳带的最优化问题，可在最小二乘框架下求解。由此，根据带限Snell定律求解各向异性带限射线的传播方向，对应地描述各向异性介质中带限波场的传播方向。如图2b所示，由xs发出的射线束，经过速度界面Γ后，对于不同方向的格林函数的波场能量不同。基于带限中心射线的射线束(红色)对应最大能量方向，描述带限波场的传播方向。

下面以该带限射线为中心射线，结合旁轴射线束构建各向异性带限射线束传播算子。将中心射线旅行时在射线束宽度内展开

(9)

式中：x0为中心射线坐标；xΩ为射线束宽度内的坐标； Δs为xΩ在中心射线上的投影与x0间的距离；r为xΩ到中心射线的距离；mr为与射线束波前曲率相关的动力学参数

(10)

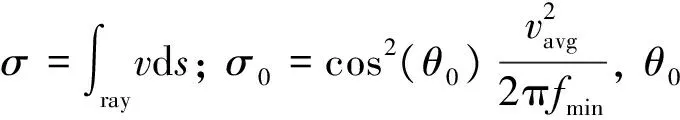
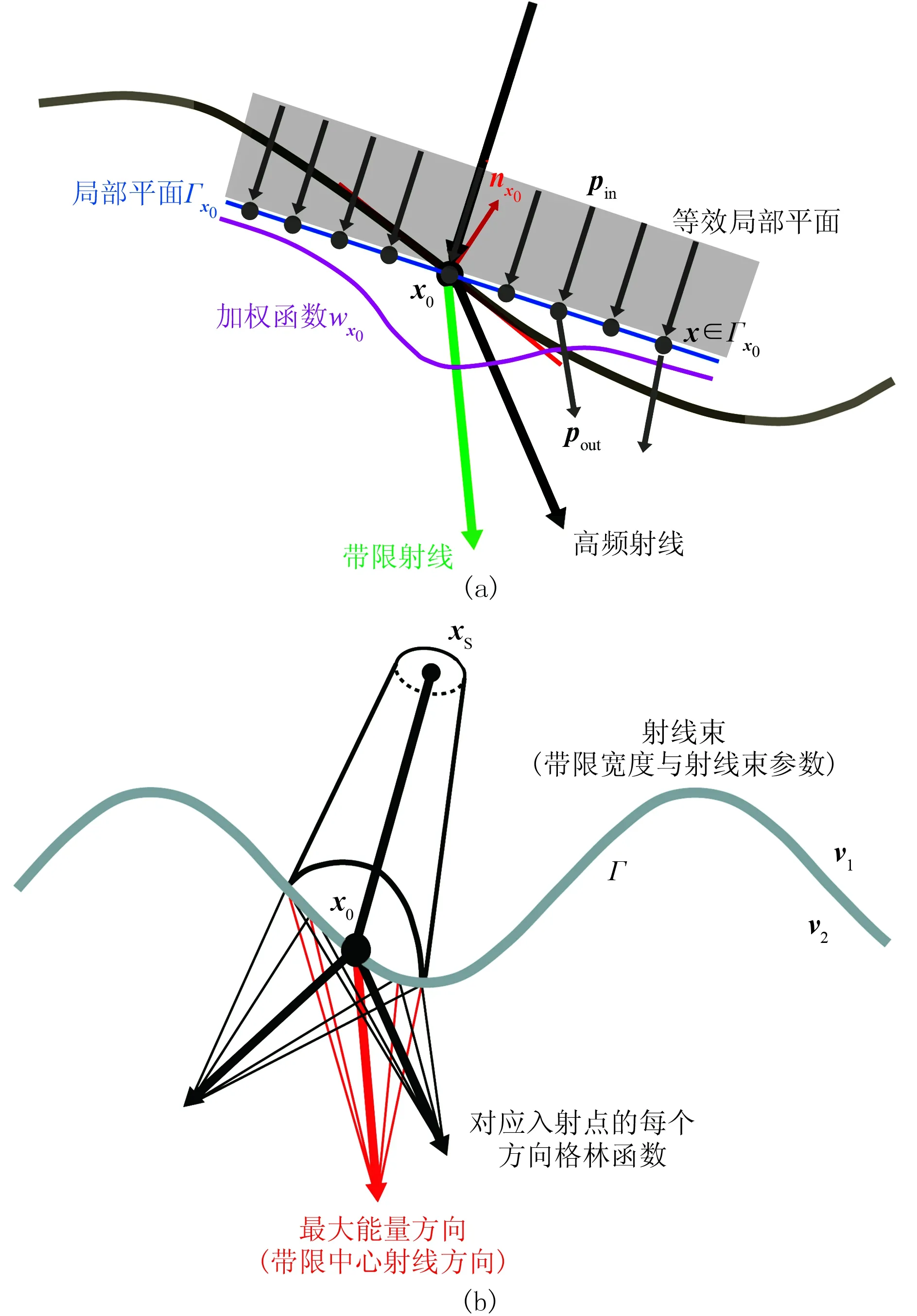
图2　带限射线追踪(a)及传播示意图(b)

地震波偏移成像可表达为地震波传播算子加上成像条件，基于各向异性带限射线束传播算子可构建各向异性带限射线束偏移算法。将传统的Kirchhoff积分偏移成像条件应用于共炮集数据的射线束偏移方程中

pr(xr0)]dΩ|τ=τs+τr

(11)

式中：x为地下成像点；Ω包含炮点xs和检波点中心点xr0的成像孔径；ps,pr为炮点和检波点中心的初始射线参数；w为成像点的加权函数[36]；d为时间域表征的局部平面波；τ为旅行时。该共炮集成像方程可在时间空间域高效实现。

3　数值实验

为验证TI介质带限射线束传播算子的有效性和正确性，本文选取四类简单模型和各向异性SEG/Hess模型进行数值实验。

首先，选取四类简单各向异性模型进行带限射线照明分析，图3为四类简单模型高频射线与带限射线照明分析，模型网格为10m×10m。对于同一模型设置相同震源坐标，分别进行TI介质的射线追踪、带限射线追踪和有限差分求解波动方程正演模拟，对比相同时刻的射线旅行时波前与有限差分计算波场快照。对比高频射线和带限射线的射线路径与波前面可知，带限射线较高频射线在模型中分布更均匀，提高了传统射线阴影区的射线覆盖率，能够提供更有效的照明。

然后，选择各向异性SEG/Hess模型对TI介质带限射线束传播算子及其对应的偏移成像方法进行照明分析和偏移脉冲响应测试。如图4所示，SEG/Hess模型中存在高速盐丘体和三个各向异性透镜体，同时模型包含陡倾断裂构造，模型网格为5m×5m。在x=8.0km处设置震源，分别进行射线追踪得到高频射线路径和带限射线路径(图5a和图5b)。对比高频射线和带限射线路径可知，带限射线在盐丘下方区域“①”、盐丘侧方各向异性透镜体区域“②”、模型断层区域“③”有更均匀的射线分布。对应地，以带限射线为中心射线构建的带限射线束进一步提高了盐下射线阴影区和各向异性透镜体的照明。相比于传统射线束偏移脉冲响应(图5c)，带限射线束偏移脉冲响应(图5d)的能量连续性更好。

图6a和6b展示了TI介质传统射线束偏移和TI介质带限射线束偏移结果，图6c和6d为图6a及图6b中矩形框内区域的放大展示。 对比箭头所示的区域，相比于TI介质传统射线束偏移，TI介质带限射线束偏移结果中对于复杂盐丘边界和陡倾断裂构造成像效果更聚焦，同相轴能量分布更均匀，对于各向异性透镜体(A、B和C)及其相邻盐丘侧边界的刻画更准确。图7a和7b分别为两种射线束方法5处的角度域成像道集(x=2.75， 6.95， 8.40，9.50，12.40km)，对比图中红色箭头标注的区域，TI介质带限局部平面波传播算子能够为对应的射线束偏移提供更有效的角度域照明，TI介质带限射线束偏移可输出质量更高的角度域共成像点道集。

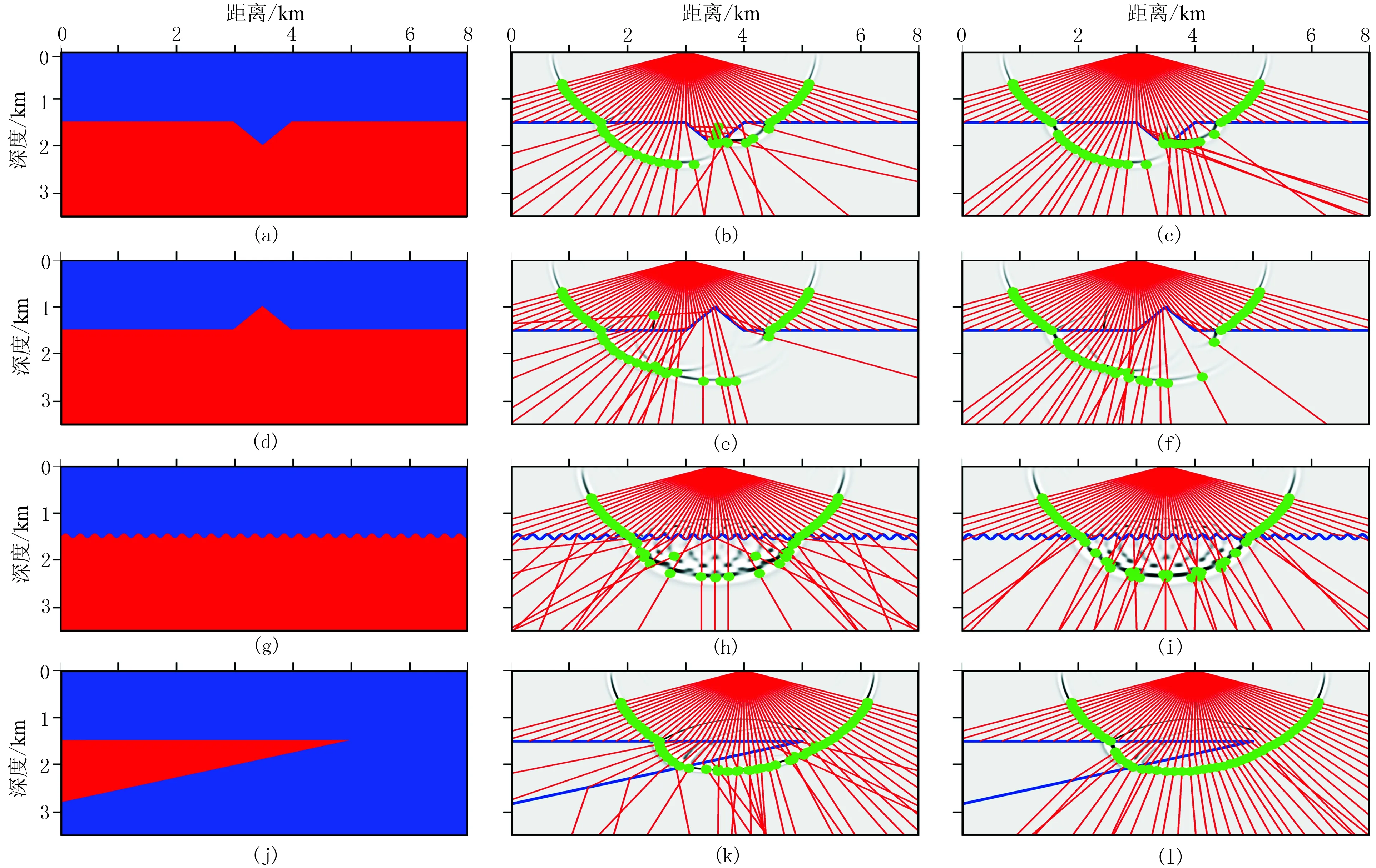
图3　四类简单模型高频射线与带限模型照明分析

(a)向斜各向异性模型； (b)图a的高频射线路径及波前面； (c)图a的带限射线路径及波前面； (d)背斜各向异性模型； (e)图d的高频射线路径及波前面； (f)图d的带限射线路径及波前面； (g)崎岖震荡各向异性模型； (h)图g的高频射线路径及波前面； (i)图g的带限射线路径及波前面； (j)楔形各向异性模型； (k)图j的高频射线路径及波前面； (l)图j的带限射线路径及波前面

各类各向异性模型中两种介质参数：vP0为2.5km/s和4.5km/s，ε为0.15和0.05，δ为0.06和0.02。模型速度界面以蓝色实线表示； 射线以红色实线表示； 射线范围-65°～65°，间隔2.5°； 0.8s旅行时波前面以绿色实心圆点表示；背景为有限差分计算的震源主频20Hz的0.8s波场快照

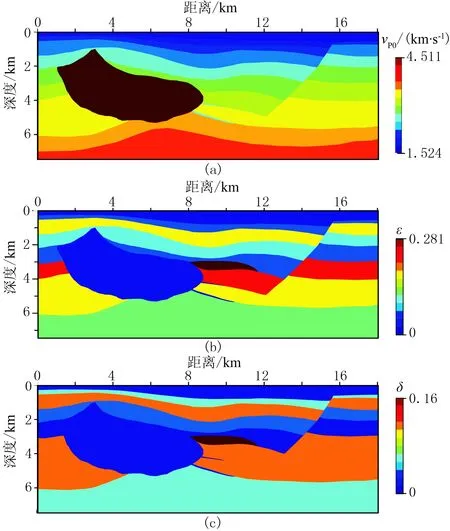
图4　SEG/Hess模型各向异性参数 (a)vP0； (b)ε； (c)δ

4　结论

在射线理论框架下，基于局部平面波假设，提出了适用于各向异性介质的带限射线束传播算子，分析了该算子对盐丘等复杂构造和各向异性结构的照明，并发展了基于该算子的带限射线束偏移方法。数值实验表明，各向异性带限射线束能够改善盐下、断裂等复杂各向异性构造的角度域照明，提高偏移剖面和角度域共成像点道集的质量。本文发展的TI介质带限波传播算子和偏移成像方法为后续基于该算子的层析反演、偏移速度分析等奠定了基础。

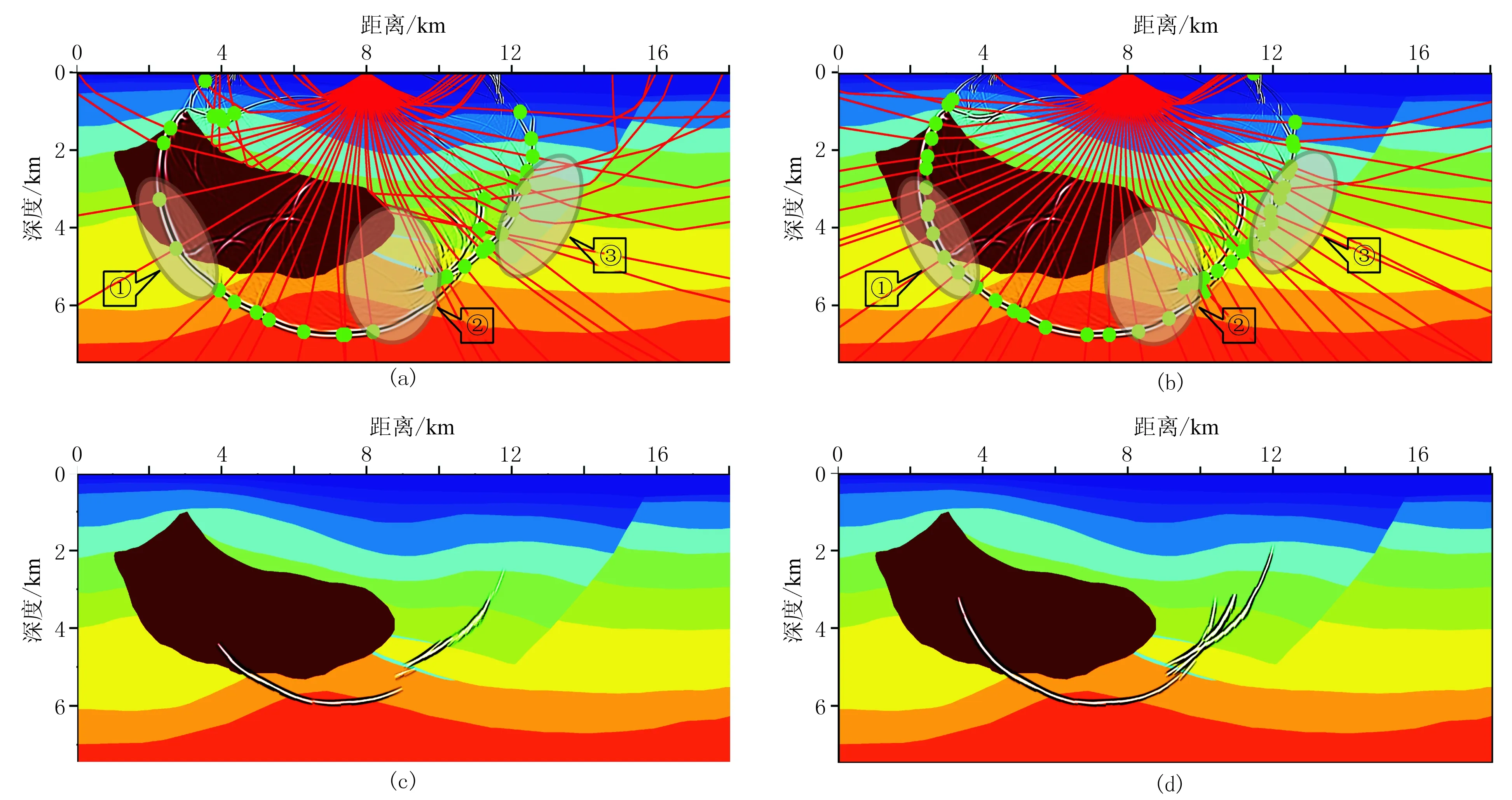
图5　TI介质射线束照明与偏移脉冲响应对比

(a)TI介质高频射线路径及旅行时波前面； (b)TI介质带限射线路径及旅行时波前面； (c)TI介质传统射线束偏移脉冲响应； (d)TI介质带限射线束偏移脉冲响应

炮点坐标(8km,0)，射线路径以红色实线表示； 初始射线角度范围-60°～60°，角度间隔2.5°； 2.4s旅行时波前面以绿色实心圆点表示；背景为有限差分正演模拟的震源主频为20Hz的2.4s波场快照。偏移脉冲响应为记录于x=8km，记录时间为4.353s的20Hz雷克子波，对应于坐标(8.0km，5.825km)的反射点感谢勘探地球物理学家协会(SEG)和Amerada Hess石油公司提供公开模型数据。

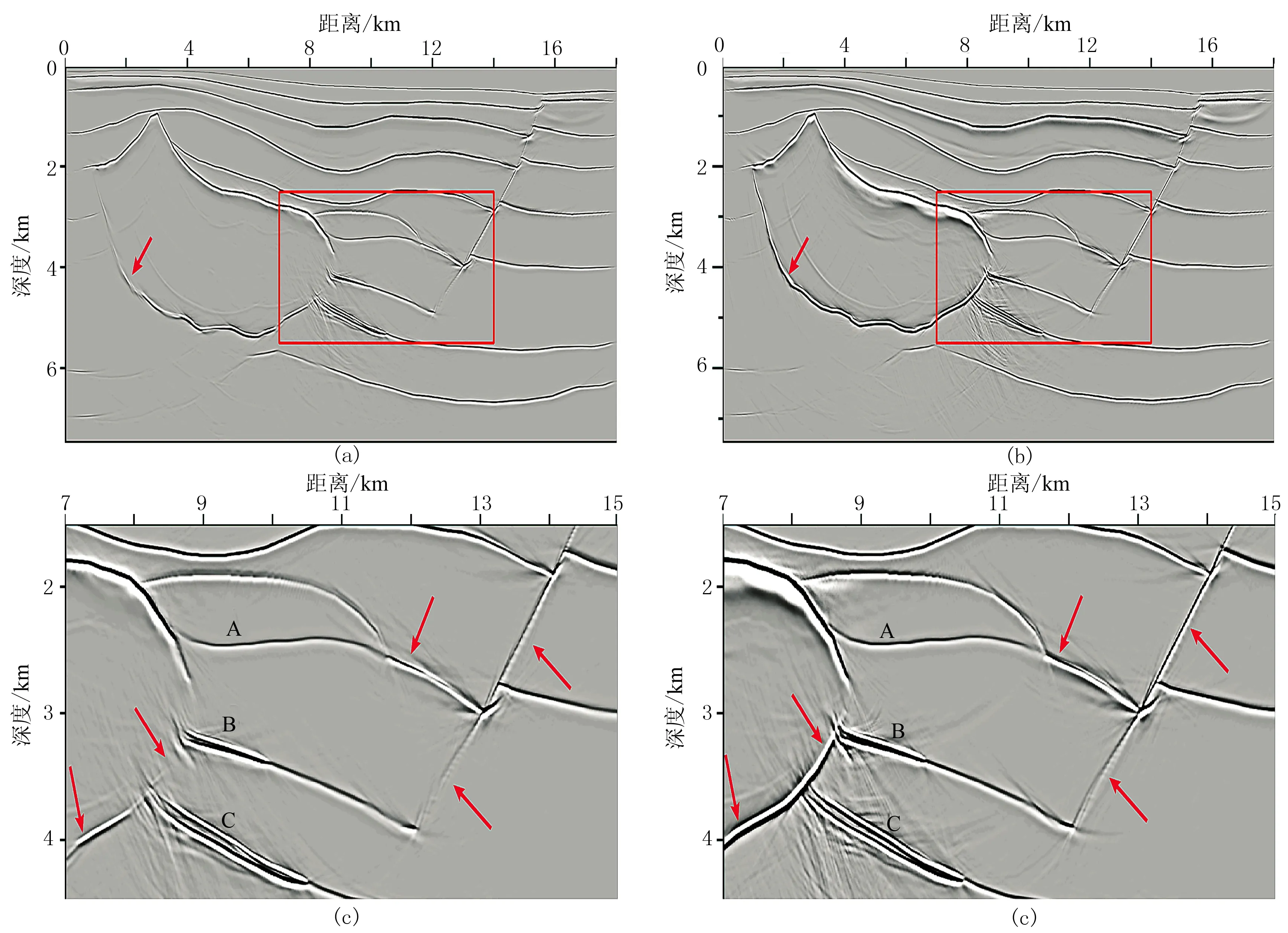
图6　TI介质射线束偏移结果对比

[1]Kravtsov Y A,Orlov Y I.Geometrical Optics of Inhomogeneous Media.Springer-Verlag,1990.

[2]Yoon K,Marfurt K J.Reverse-time migration using the Poynting vector.Exploration Geophysics,2006,37(1)：102-107.

[3]Hu J,McMechan G A,Guan H.Comparison of methods for extracting ADCIGs from RTM.Geophysics,2014,79(3)：S89-S103.

[4]Foreman T.A Frequency Dependent Ray Theory[D].The University of Texas at Austin,1987.

[5]Protasov M,Gadylshin K.Exact frequency dependent rays on the basis of Helmholtz solver.SEG Technical Program Expanded Abstracts,2015,34：3739-3743.

[6]Biondi B.Solving the frequency dependent eikonal equation.SEG Technical Program Expanded Abstracts,1992,11：1315-1319.

[7]Lomax A.The wavelength-smoothing method for approximating broad-band wave propagation through complicated velocity structures.Geophysical Journal International,1994,117(2)：313-334.

[8]Zelt C A,Chen J.Frequency-dependent traveltime tomography for near-surface seismic refraction data.Geophysical Journal International,2016,207(1)：72-88.

[9]Chen J,Zelt C A.Comparison of full wavefield syn-thetics with frequency-dependent traveltimes calculated using wavelength-dependent velocity smoothing.Journal of Environmental and Engineering Geophy-sics,2017,22(2)：133-141.

[10]Protasov M I,Yarman C E,Nichols D et al.Frequency-dependent ray-tracing through rugose interfaces.SEG Technical Program Expanded Abstracts,2011,30：2992-2996.

[11]Yarman C E,Cheng X,Osypov K et al.Band-limited ray tracing.Geophysical Prospecting,2013,61(6)：1194-1205.

[12]刘少勇,韩冰凯,顾汉明等.带限射线束传播算子及偏移方法.石油地球物理勘探,2017,52(5)：948-955.

Liu Shaoyong,Han Bingkai,Gu Hanming et al.Study on band-limited beam propagator and migration method.OGP,2017,52(5)：948-955.

[13]Isaac J H,Lawton D C.Image mispositioning due to dipping TI media:A physical seismic modeling study.Geophysics,1999,64(4)：1230-1238.

[14]Fowler P J,Du X,Fletcher R P.Coupled equations for reverse time migration in transversely isotropic media.Geophysics,2010,75(1)：S11-S22.

[15]Delaney S J,O’Brien G S,Short R et al.Tilted transverse isotropic reverse time migration with angle gathers:Implementation and efficiency.Geophysics,2016,81(6)：S419-S432.

[17]Alkhalifah T.An acoustic wave equation for aniso-tropic media.Geophysics,2000,65(4)：1239-1250.

[18]Kumar D,Sen M K,Ferguson R J.Traveltime calculation and prestack depth migration in tilted transversely isotropic media.Geophysics,2004,69(1)：37-44.

[19]Qian J,Symes W.Finite-difference quasi-P traveltime for anisotropic media.Geophysics,2002,67(1)：147-155.

[20]Sun J,Sun Z,Han F.A finite difference scheme for solving the eikonal equation including surface topography.Geophysics,2011,76(4)：T53-T63.

[21]Vanelle C,Gajewski D.True-amplitude Kirchhoff depth migration in anisotropic media:The traveltime-based approach.Geophysics,2013,78(5)：WC33-WC39.

[21]Liu S,Wang H,Yang Q et al.Traveltime computation and imaging from rugged topography in 3D TTI media.Journal of Geophysics and Engineering,2014,11(1)：1-9.

[23]Hill N R.Gaussian beam migration.Geophysics,1990,55(11)：1416-1428.

[24]Hill N R.Prestack Gaussian-beam depth migration.Geophysics,2001,66(4)：1240-1250.

[25]邓飞,刘超颖,赵波等.高斯射线束正演与偏移.石油地球物理勘探,2009,44(3)：265-269.

Deng Fei,Liu Chaoying,Zhao Bo et al.Gaussian beams forward simulation and migration.OGP,2009,44(3)：265-269.

[26]李振春,岳玉波,郭朝斌等.高斯波束共角度保幅深度偏移.石油地球物理勘探,2010,43(3):360-365.

Li Zhenchun,Yue Yubo,Guo Chaobin et al.Gaussian beam common angle preserved-amplitude migration.OGP,2010,45(3)：360-365.

[27]Zhu T,Gray S H,Wang D.Prestack Gaussian-beam depth migration in anisotropic media.Geophysics,2007,72(3)：S133-S138.

[28]韩建光,王赟,张晓波等.VTI介质高斯束叠前深度偏移.石油地球物理勘探,2015,50(2)：267-273.

Han Jianguang, Wang Yun, Zhang Xiaobo et al.Gaussian beam prestack depth migration in VTI media.OGP,2015,50(2)：267-273.

[29]刘强,张敏,李振春等.各向异性介质共炮域高斯束偏移.石油地球物理勘探,2016,51(5)：930-937.

Liu Qiang,Zhang Min, Li Zhenchun et al.Common-shot domain Gaussian beam migration in anisotropic media.OGP,51(5)：930-937.

[31]Woodward M J.Wave-equation tomography.Geophysics,1992,57(1)：15-26.

[32]Chapman C H.Fundamentals of Seismic Wave Propagation.Cambridge University Press,2004.

[33]Thomsen L.Weak elastic anisotropy.Geophysics,1986,51(10)：1954-1966.

[34]Jiang B,Wang H Z,Liu S Y.A phase-velocity based ray tracing system for anisotropic media.76th EAGE Conference & Exhibition,Amsterdam,2014,We G105 15.

[35]Liu S,Wang H,Feng B.The characteristic wave decomposition and imaging in VTI media.Journal of Applied Geophysics,2015,115(13)：51-58.

[36]Hu C,Stoffa P L.Slowness-driven gaussian-beam prestack depth migration for low-fold seismic data.Geophysics,2009,74(6)：WCA35-WCA45.