基于邻域粗糙集的转子故障数据属性约简

2018-04-09何敬举赵荣珍赵孝礼孙业北

机械设计与制造工程 2018年3期

何敬举，赵荣珍，赵孝礼，孙业北

(兰州理工大学机电工程学院，甘肃兰州　730050)

随着现代工业技术的不断发展, 越来越多的旋转机械被应用到企业的生产中, 这对旋转机械故障诊断技术不断提出新的要求[1]。机械故障诊断中最为关键的步骤是提取信号故障特征[2-3]。特征提取又称属性约简或维数约简，从数学的角度考虑，就是通过某种方法使新数据的维数小于等于原数据的维数，新的数据在某种评判标准下最大限度地保留原始数据的特征[4]。属性约简主要是为了解决高维数据计算的复杂性和准确性问题，目的是消除冗余和不相关属性对计算过程和最终结果造成的影响，降低计算复杂度，减少计算时间[5]。在现实世界中，数据数量庞大且数据质量较低，使得许多数据存在不确定性[6]。如何从庞大的数据集中提取出有效的切合实际物理意义的故障特征，进而提高故障诊断的准确性和缩短诊断时间是当前需要研究的问题。

粗糙集是一种从不完备、不完整数据集中获取知识的数学方法，近年来被国内外专家用在不同领域且都取得了很好的效果[7-8]，在故障诊断中也被广泛应用。文献[9]采用粗糙集理论对离散化后的决策表进行约简,建立故障诊断规则决策表,能够简化决策表属性约简的难度,使诊断变得更加简便。文献[10]将粗糙集和数据库神经网络结合用来诊断液压机故障，提高了诊断准确性。文献[11]首次对粗糙集理论用于旋转机械状态监测与故障诊断系统知识库构造、实现在线智能知识获取与知识发现及归纳推理进行了研究，并且给出了理论框架。在此基础上,文献[12]将变精度粗糙集用在汽轮机组的故障诊断上，建立了决策表，证实了此方法可以有效获得故障特征属性。为了解决连续属性离散化过程中属性丢失的问题，文献[13]首次在国内提出邻域粗糙集概念，并给出了前向贪心算法，证实了邻域粗糙集在对连续属性约简时能够获得更高的精确度和准确度。文献[14]将多小波包和邻域粗糙集结合在一起建立了故障诊断模型，验证了邻域粗糙集能够从大量的原始特征中选择出敏感特征，减小分类算法的复杂性，提高分类的准确性，证实了该模型在复合故障诊断中具有显著优势。

然而文献[14]只对以峰值、均值等信号时域特征构成的数据集进行了分析，没有对反映信号本质的频域特征集进行分析。为了更好地获取反映故障本质的属性以及减少连续属性离散化过程中属性的丢失，本文将频域特征信息和邻域粗糙集结合起来对故障特征进行提取，证明了该方法能够获得旋转机械典型故障的关键属性以及准确的决策规则。

1　原理介绍

1.1　邻域粗糙集理论

1982年波兰科学家PAWLAK提出了粗糙集理论[15]，将研究对象的全体称为论域，利用不可分辨关系将论域粒化为若干互斥的等价类，作为描述论域中任意概念的基本信息粒子。LIN[16]在1988年提出了邻域模型的概念，将邻域理解为基本信息粒子，通过空间中点的邻域来粒化论域空间。胡清华等[13]利用拓扑空间中球形邻域的概念构造了基于邻域粗糙集模型的数值特征属性选择算法。邻域粗糙集的基本概念如下：

1)定义(度量)在一给定的N维实数空间Ω中，Δ=RN×RN→R，则称Δ为RN上的一个度量(距离)，若Δ满足以下条件：

①Δ(χ1,χ2)≥0,其中当且仅当χ1=χ2时等号成立， ∀χ1,χ2∈RN；

②Δ(χ1,χ2)=Δ(χ2,χ1)， ∀χ1,χ2∈RN；

③Δ(χ1,χ3)≤Δ(χ1,χ2)+Δ(χ2,χ3)，∀χ1,χ2，χ3∈RN。

则称(Ω，Δ)为度量空间，Δ(χi,χj)为距离函数，表示元素χi和元素χj之间的距离。显然这里合理地给出了元素空间中距离的概念。

2)定义(邻域)在给定空间Ω上的非空有限集合U={χ1,χ2,…,χn},对∀χi的邻域δ定义为：

δ(χi)={χ|χ∈U,Δ(χ,χi)≤δ},δ≥0

同样给定邻域关系N,和原始粗糙集理论相类比可得邻域近似空间NS=(U,N)的上近似、下近似和近似边界分别为：

(1)

NX={χi|δ(χi)⊆X,χi∈U}

(2)

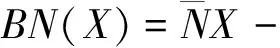
(3)

正域和负域分别为：

Pos(X)=NX

(4)

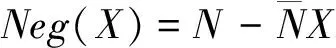
(5)

3)定义(领域决策系统)给定一邻域决策系统NDS=(U,A∪D,n)，其中A为条件属性，D为决策属性，决策属性D将论域U划分为n个等价类(X1，X2，…，Xn)，对于∀B⊆A，则决策属性D关于条件属性B的上、下近似分别为：

(6)

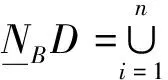
(7)

类比可得邻域决策系统的边界域、正域和负域分别为：

(8)

PosB(D)=NBD

(9)

(10)

决策属性D对子集条件属性B的属性依赖度为：

(11)

若条件属性a∈B，则a对决策属性D的重要度为：

Sig(a,B,D)=γB(D)-γB-{a}(D)

(12)

式中：γB(D)为决策属性D对子集条件属性B的属性依赖度。

1.2　转子故障诊断频谱分析法

用于旋转机械设备故障诊断的方法有很多，常用的方法按检测手段分为振动检测诊断法、噪声检测手段法、温度检测诊断法、声发射检测诊断法、油液分析诊断法等。其中振动检测诊断法主要采用时域分析、频域分析、时序分析、时频域分析等方法来分析采集到的振动信号，发现振动变化的原因，从而更可靠、准确地发现故障特征。实际工程中的信号是杂乱无章的且夹杂着噪声，把信号从时域转到频域来分析能够把混叠在一起的信号分离出来，更能够找出信号的本质。

在数字信号处理领域用到的一种很基本、很重要的方法就是傅立叶变换。傅立叶变换将原来难以处理的时域信号转换成了易于分析的频域信号，从而可以利用一些工具对这些频域信号进行处理、加工。最后还可以用傅立叶反变换将这些频域信号转换成时域信号。傅立叶变换是一种特殊的积分变换，其基本公式为：

(13)

式中：F(ω)为f(t)的像函数；f(t)为F(ω)的像原函数。

频谱分析可以快速并准确地找出故障部件的故障所在，也可以进行点检定修，确保机械设备不存在安全隐患。频谱分析还能克服外界对测试的干扰，较为准确地分析数据，得到确切的故障诊断信息。因为利用振动信号进行分析的诊断技术其本身在机械设备领域中有很好的应用前景[17]，所以利用粗糙集理论在反映信号本质的频域数据库中进行知识的获取、属性的约简能够获得更好的特征属性和更加准确的决策规则。

1.3　频域论域内的邻域粗糙集决策表

1.3.1频域决策表理论

在旋转机械故障诊断中，大量理论和试验证明，不同的故障类型在它们的频谱图上有着不同的表现，特别是在频谱图的各个倍频上更有显著性的差异。从夹杂着噪声、非平稳信号的海量原始故障数据集中提取出有效特征从而做出决策是一件非常困难的事，而邻域粗糙集提供了一种从连续的或者符号型的数据集中有效、准确获取知识的方法[13]，所以本文提出的以工频f的各个倍频为条件属性，以转子不平衡、不对中等故障为决策属性建立邻域粗糙集决策表是可行的[12，14]。首先利用式(13)对故障振动信号进行频谱分析，读取各倍频下对应的谱峰值建立故障数据库，然后利用式(14)得到邻域半径δ，之后就是进行如下的属性约简。

1.3.2频域决策表属性约简程序

Step1，输入决策系统NDS=(U,A∪D)，邻域半径δ集合，重要度下限；

Step2，初始化约简集合red=Ø，样本smp=U;

Step4，选择ak使正域Posak(D)最大；

Step5，利用式(12)计算属性重要度Sig(ak,red,D)；

Step6，如果Sig(ak,red,D)大于设定的下限值，则输出约简结果red，否则，记录k值,令：red=red+ak，S=S-Posak，然后返回Step3。

2　实验与讨论

2.1　实验

本文采用双跨转子实验台采集的振动信号集合作为实验对象，采集信号的传感器为电涡流位移传感器，转速为2 800r/min，采样频率为5 000Hz，信号截取长度为1024字节，模拟转子不平衡、转子不对中和碰磨3种故障状态。通过式(13)对振动信号的处理计算出设备信号1,2,3,4,5,6倍频处的幅值。令A1,A2,A3,A4,A5,A6分别代表1,2,3,4,5,6倍频，作为条件属性，以转子不平衡、转子不对中和转子碰磨3种故障类型为决策属性，取16个样本为训练样本建立频域邻域粗糙集决策表(表1)，论域内的每个元素代表着对应故障和倍频下的频谱幅值。然后用数字1代表转子不平衡，2代表转子不对中，3代表转子碰磨，对决策表进行归一化处理，因为在邻域粗糙集中存在数量级和量纲的差异，为了获得更精确的处理结果需要对数据进行归一化处理[13]。这里对决策属性也进行了归一化，最后一列为决策属性归一化后的结果(表2)。为了防止大数吃小数的现象，应分别对每一列进行归一化，其中决策属性也可以不进行归一化。之后按如下公式计算邻域半径：

δ(Ai)=Std(Ai)/λ(i=1,2,…,6)

(14)

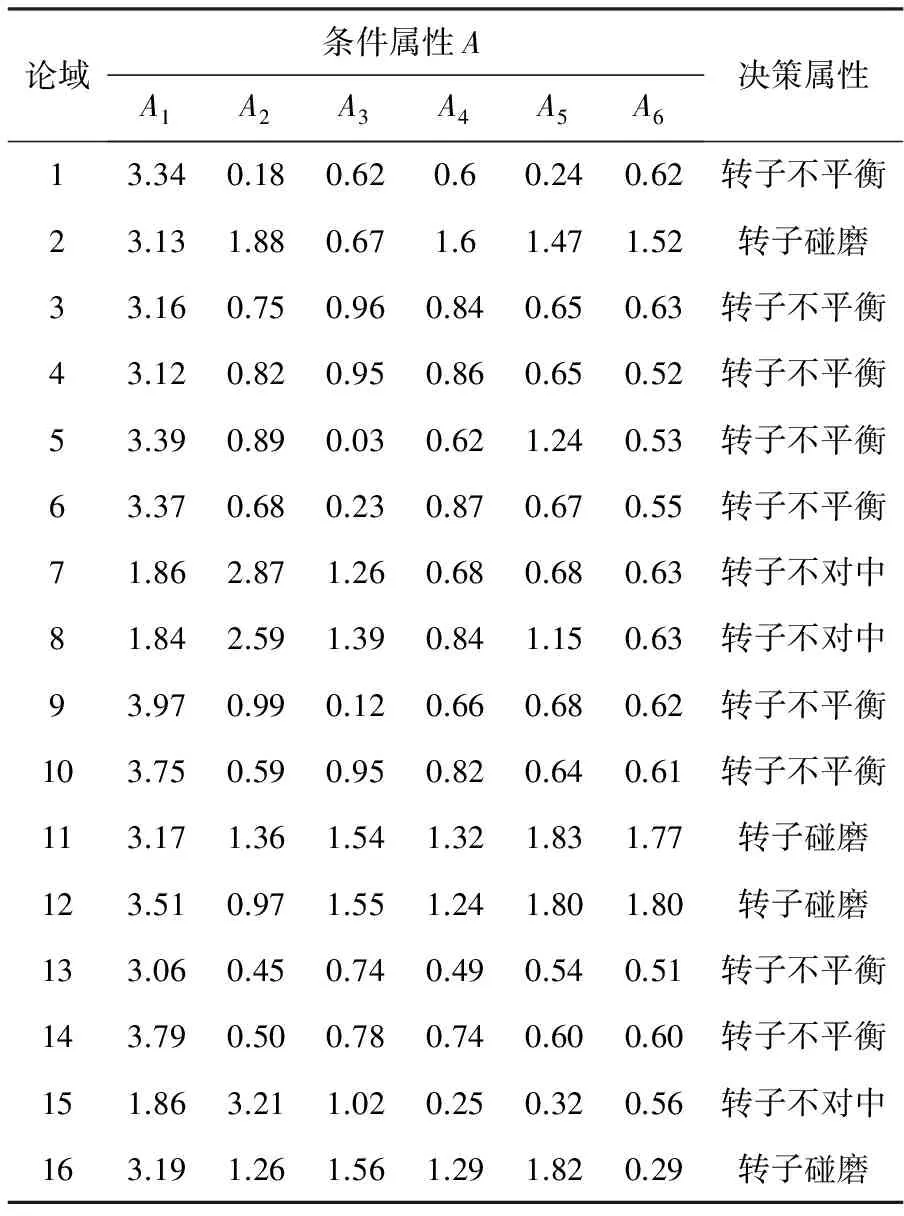
表1　频域邻域粗糙集决策表

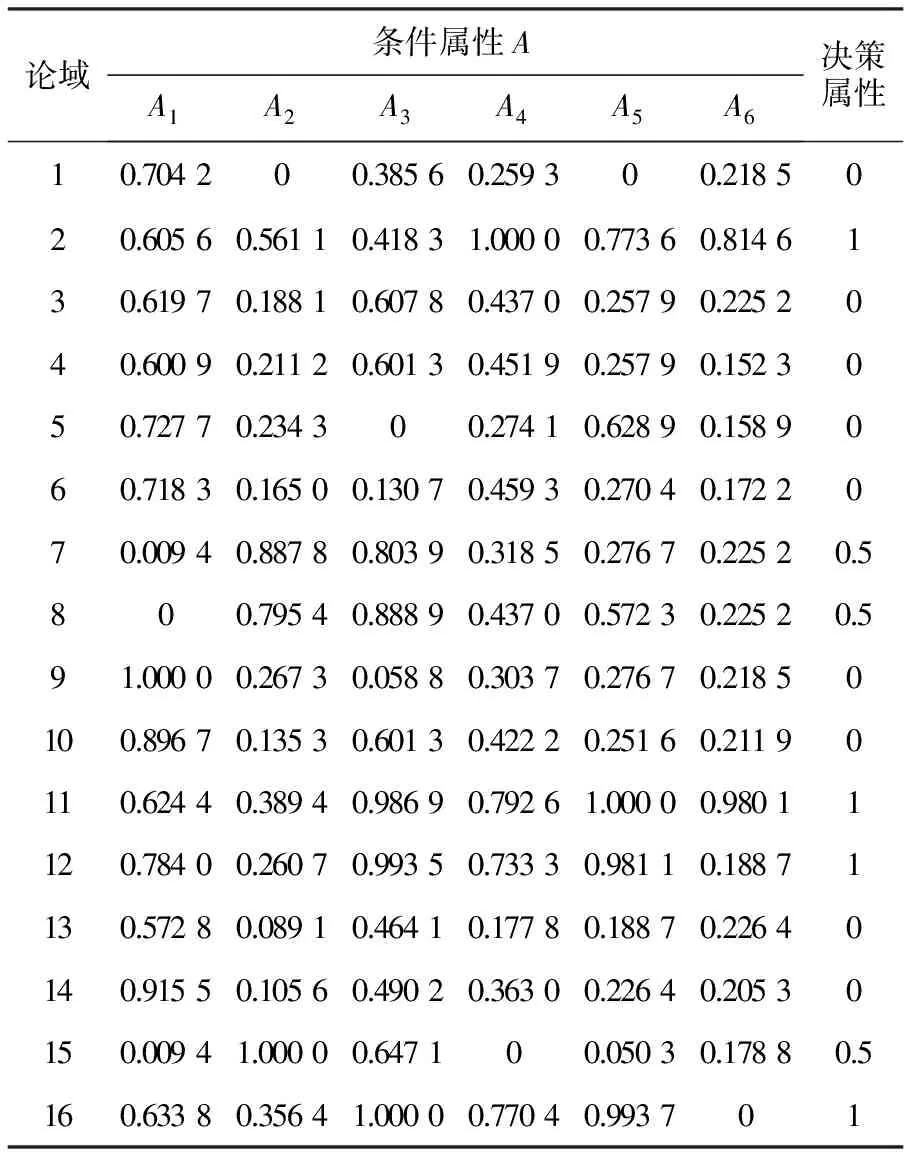
表2　决策表归一化后结果

式中：Std(Ai)为每一列条件属性的标准差；λ为一设定的参数，用来根据分类精度调整邻域大小。这样就可以根据邻域粗糙集的定义，以某个样本为中心，以邻域半径大小为半径画圆来确定邻域。之后再根据相关定义对决策表进行属性约简、特征提取等相关计算。整个数据处理过程如图1所示。邻域粗糙集的约简结果和邻域半径的大小与设定的重要度下限有关，存在合适的邻域半径值域使约简出来的结果最合适。重要度下限一般设定为接近于0的数[13]。表3为当λ=0.5、重要度下限为0.001时约简得到的属性以及各属性对应的重要度值。由于决策树C4.5算法能够有效地处理连续属性和缺省不完整数据，所以本实验采用决策树C4.5来获取决策规则。实验平台为Windows 7系统下的基于Java环境下开源的WEKA软件。图2为由原始决策表得到的决策树，图3为经邻域粗糙集约简、删除掉冗余属性后得到的决策树。代入16个测试样本进行验证，正确率分别为81.25%和87.50%。

图1　数据集处理流程图

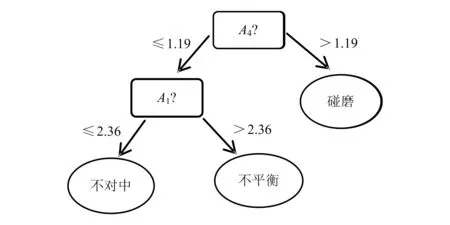
图2　原始数据集决策规则

图3　邻域粗糙集约简后决策规则

表3　约简剩余属性及对应重要度

2.2　讨论

由图2可得，原始故障数据集在经过决策树C4.5离散化处理后得到的属性重要度最大为4倍频，这和实际测量的实验结果的差异性相差较大。在实际的测量过程中，转子的各种故障在频谱图中主要表现为2倍频、1倍频、1/2倍频和1/3倍频的谱峰值上的差异，随着倍频数的增高，差异性越来越弱化。可见，在对连续属性数据处理的过程中，特别是对实际工程复杂信号的分析中，离散化的过程很容易导致重要的信息丢失，从而使分析得出的结果表面上只适合单纯的数据，但是不符合实际情况。

由表3可得，经邻域粗糙集约简后得到的重要属性是2倍频、1倍频、3倍频和5倍频，这和试验中对各种故障做频谱分析时得到的谱峰值的差异性比较相似。由图3也可看出，由1倍频和2倍频这两个属性特征就能基本确定故障类型。回到表1，和其他条件属性相比，显然2倍频下的属性特征对3种故障类型差异性的表示更明显。对比论域为12这一行转子碰磨下的2倍频值0.97和其他碰磨下的2倍频值，可以看出相差比较大，如果这是测量误差所致，那就可以单独用2倍频这一个条件属性下的值来区分3种故障类型。对比图2和图3可见，原始故障数据集经过邻域粗糙集约简后，删除了影响数据分析的冗余属性，能够得到更加准确和更加符合实际物理意义的特征值。在后续用测试样本进行验证时，约简后的故障分类正确率也大于约简前的分类正确率。

3　结束语

本文将邻域粗糙集概念用在了旋转机械故障诊断的频域分析当中，并以各倍频为条件属性、以故障类型为决策属性建立了决策表来获取决策规则。结果表明，基于邻域粗糙集理论的原始故障数据集的属性约简能有效地避免在对具有实际物理意义的连续属性离散化的过程中造成的关键属性的丢失。实验结果表明该方法能够有效地获得典型故障的关键属性和更加准确的决策规则。

参考文献：

[1]罗邦劼. 旋转机械故障诊断技术的研究现状及发展趋势[J]. 机电产品开发与创新，2008(3)：85-86.

[2]PENG Z,CHU F, HE Y. Vibration signal analysis and feature extraction based on reassigned wavelet scalogram[J]. Journal of Sound and Vibration,2002，253(5): 1087-1100.

[3]RANDALL R B. Detection and diagnosis of incipient bearing failure in helicoper gearboxes[J]. Engineering Failure Aanlysis,2004，11(2): 177-190.

[4]冯宗翰. 特征选择新算法研究[D]. 无锡:江南大学, 2011.

[5]孙丽萍, 陈果, 陈立波, 等. 基于 KPCA 的航空发动机滑油滤磨屑图像识别[J]. 机械科学与技术, 2010, 29(6):731-736.

[6]杨传健,葛浩,汪志圣. 基于粗糙集的属性约简方法研究综述[J]. 计算机应用研究，2012(1)：16-20.

[7]马文萍,黄媛媛,李豪,等. 基于粗糙集与差分免疫模糊聚类算法的图像分割[J]. 软件学报， 2014(11)：2675-2689.

[8]叶回春,张世文,黄元仿,等. 粗糙集理论在土壤肥力评价指标权重确定中的应用[J]. 中国农业科学，2014(4)：710-717.

[9]陈小青,刘觉民,黄英伟,等. 采用改进人工鱼群优化粗糙集算法的变压器故障诊断[J]. 高电压技术，2012(6)：1403-1409.

[10] 李雪冬. 基于粗糙集神经网络液压机故障诊断专家系统的研究开发[D]. 合肥：合肥工业大学， 2012.

[11] 赵荣珍,孟凡明,张优云. 基于粗糙集知识获取的转子轴承系统故障诊断知识库构造研究[J]. 润滑与密封，2004(4)：25-26.

[12] 邓林峰,赵荣珍,冯如只,等. 基于特征选择和变精度粗集的属性约简方法及其应用[J]. 机械科学与技术， 2010,29(10)：1412-1416.

[13] 胡清华,于达仁,谢宗霞. 基于邻域粒化和粗糙逼近的数值属性约简[J]. 软件学报，2008, 19(3):640-649.

[14] 瞿金秀,张周锁,何正嘉. 基于多小波包和邻域粗糙集的故障诊断模型[J]. 振动、测试与诊断，2013(增刊1)：137-140.