基于显式模型预测控制的大规模路网交通信号控制方法

陆　可，杜萍萍，邹启鸣，何天嘉

(安徽工业大学管理科学与工程学院，安徽 马鞍山　243000)

近年来，随着社会经济的不断发展，日益恶化的城市交通状况及其引发的一系列问题引起了人们越来越广泛的关注。同时，由于城市交通路网规模越来越大，交叉路口之间的时空关联性越来越强，对单个交叉路口的控制已经不能从根本上缓解交通拥堵问题[1]。虽然加强基础设施建设可以直接有效地解决城市交通拥堵问题，但是会受到资金、时间和空间上的严重制约[2]。为此，基于现有交通基础设施，以路网中的某个区域(或者整个路网)为控制对象，以区域的整体交通效益为优化目标，对区域内所有交叉路口进行协调控制，已经成为提高交通信号控制系统运行效率的主要方法[3-4]。

大量的研究表明，实时信号控制比固定时间控制能更有效地缓解交通拥堵[5]。自20世纪80年代初以来，研究者们已经开发了大量交通响应型城市控制系统来解决交通拥堵问题，如SCOOT[6]和SCATS[7]系统，这两个系统基于实时交通状态的自适应响应控制方法在线优化信号配时；还有一部分研究是基于短时交通流预测策略的自适应交通信号控制模型，如OPAC[8]和RHODES系统[9]，其可以通过交通系统的控制模型来预测未来交通状况。

以上提到的交通信号控制系统已成功地应用于世界各地。然而大规模网络的复杂性，使协调控制整个路网变得十分困难，模型预测控制(model predictive control，MPC)方法有效地提升了大规模交通路网中的信号控制效率，引起了人们的高度重视[10]。该方法基于模型预测未来的交通状态，并在线滚动优化交通系统的路网状态，得出最优信号控制方案。

MPC方法在交通系统领域的应用得到了广泛的关注。ABOUDOLAS等[11]将交通优化问题重新设计成一个二次规划问题，并将其嵌入到滚动优化控制方案中，可以显著降低在线计算复杂度。此外，根据宏观交通模型，基于准确的城市交通模型的MPC控制器可以处理各种复杂的交通场景[12-13]。考虑到大型城市交通网络的复杂性，分布式控制旨在提升MPC控制器的效率[14]。如，LIN等[15-16]设计了一种用于交通流控制的多智能体MPC框架，将集中式模型预测控制问题分解为一组由分布式智能体解决的耦合子问题。此外，考虑到不同智能体之间的控制优先级，ZHOU等[17]提出了使用基于拥塞程度的串行方案的多智能体控制方法，可以基于每个分区的拥塞程度来先后控制不同的智能体。

交通信号控制系统是一个典型的多变量、多约束、非线性的复杂大系统，MPC方法在处理该类系统的控制问题时具有诸多优势[18]。然而，当预测模型规模较大时，滚动优化需要消耗大量的时间，影响了MPC方法在一些状态快速变换的场景中的应用。针对交通信号控制系统对实时性的要求，本文拟在讨论多参数规划方法的基础上，将显式模型预测控制(explicit model predictive control，EMPC)方法引入区域交通管理问题中[19]。与传统MPC法相比，EMPC法首先通过离线计算对交通系统的状态区域进行凸划分，并得到每个状态分区上相应的最优反馈控制律。在线优化时，只需确定当前时刻系统状态所处的分区并按照该分区上的最优控制律进行简单的线性计算，就可以得到当前时刻的最优信号控制策略，大幅度减少在线优化的时间[20-21]。

本文基于store-and-forward方法建立交通信号控制模型[2]，并将EMPC方法应用到路网交通信号协调控制问题的求解中。据悉，目前的研究还缺乏将EMPC方法应用于交通优化的控制系统的深入探讨。在EMPC框架中，通过引入多参数规划方法，将交通系统的优化控制问题归结为求解相应的数学规划问题[22-23]，用离线计算的方式来凸划分系统的状态区域并得到各个状态分区所对应的分段仿射最优显式控制律[24-25]，通过在线查找状态分区表确定当前状态值所在的分区，进而获得相应的最优控制律并通过线性计算实时获取信号控制方案。

1　研究基础与相关技术

本文基于EMPC方法，在考虑未来交通状态变化的基础上，完善交通信号控制，最终实现对整个路网的优化。为了预测交通流状态，进一步优化交叉路口的信号配时方案，首先介绍了一种广泛用于大型城市网络中的交通控制模型——存储转发模型(store-and-forward model)，该模型以简化的方式描述路网交通流量的变化过程。

如图1所示的两个信号交叉口之间的路段z的动态交通流可以描述为：

xz(k+1)=xz(k)+T[qin,z(k)-qout,z(k)+ez(k)]

(1)

式中：xz(k)是在离散时刻k处路段z中的车辆的数量；在时间间隔[kT,(k+1)T]期间，qin,z(k)为路段z车辆流入的车流率，qout,z(k)为路段z车辆流出的车流率，ez为路段z上的扰动；k为离散时间步长指数；T为离散时间步长。

图1　路段z的交通流

根据定义，有以下约束：

∑i∈Figj,i+Lj≤C

(2)

式中：gj,i为交叉路口j在第i个相位处的绿灯时间；C为路网中每个交叉路口信号设置的周期时间，在本文中假设T=C。此外，交叉路口j的信号配时(包括丢失时间Lj)方案中固定数量的相位是属于相位集合Fi。不等式(2)可以用于在高度拥塞的情况下允许交叉路口信号灯处于全红状态。因此式(1)中的qin,z(k)和qout,z(k)表示为：

qin,z(k)=∑w∈Ijτw,zqout,w(k)

(3)

(4)

式中：Gz(k)为路段z的流出方向的绿灯时间，计算公式为Gz(k)=∑i∈vzgj,i(k)，vz为路段z上具有通行权的一组相位集合；sz为路段z在绿灯时间内的饱和流出量；qout,w(k)为路段z的进口道处不同方向上车辆的流入率。在该交通模型中，令Ij为通过交叉路口j流入某路段的车流集合，则τw,z为在Ij中从路段w(w∈Ij)流入路段z的车流转向率。将式(3)和(4)代入式(1)，替换路段的流入率和流出率，式(1)变为如下形式：

(5)

式中：sw为路段z在绿灯时间内的饱和流入量；uw(k)为路段z的进口道处不同方向上的绿灯时间。本文的研究目标是计算最优信号控制率uz，即绿灯时间，以最大限度地减少区域路网的车流量。对于交通网络中的所有路段，推广路段z上的车流动态方程(5)，整合后获得描述区域交通路网在离散时间上的交通流变化的状态空间矩阵方程：

x(k+1)=Ax(k)+Bu(k)+e(k)

(6)

式中：x(k)为网络中所有路段上车辆数目的状态向量；u(k)为控制输入向量(由所有绿色时间gj,i组成)；e(k)为非受控车流量的干扰向量；状态矩阵A是一个单位矩阵；B为控制输入矩阵，由两个元素组成，即转向率τ和饱和流量s。

2　基于显式模型预测控制的交通信号控制

传统的模型预测控制方法已经在包括交通信号控制等领域得到了深入的讨论和实践，然而由于其自身需要反复地在线优化，使得模型预测控制技术只能适用于系统动态变化较慢的场合。同时，为了保证闭环预测控制系统的稳定性、可行性等要求，通常需要在预测控制系统的设计阶段就考虑系统的性能要求，并引入与这些性能要求对应的额外约束条件。这些人为添加的约束条件，往往会减小闭环预测控制系统的可行区域，导致控制性能的下降和计算复杂性的增加。这些问题，限制了模型预测控制在交通系统特别是大规模路网的信号控制问题中的应用。

本文将EMPC引入大规模交通路网的交通信号控制问题中，以弥补目前模型预测控制的不足。EMPC将多参数规划理论引入到线性时不变对象的约束二次优化控制问题的求解中，对系统的状态区域(即参数区域)进行凸划分，离线计算得到对应每个状态分区上的状态反馈最优显式控制律，并建立显式模型预测控制系统。在线计算过程只需要查找当前状态所对应的分区，就可以获得相应的最优控制律，进而确定当前所需要的控制量。由于EMPC不需要反复在线优化，计算速度显著提升，从而可以满足控制的实时性要求。

2.1　交通优化模型

在交通系统中，信号配时控制应根据相关的交通流量的需求进行设计。线性二次调节器(LQR)理论的主要优点是实现了交通信号控制实时计算的简单性。为此，本文选用如下线性二次模型作为交通信号控制模型。

s.t.xt+k+1|t=Axt+k|t+But+kk≥0

(7)

0≤xt+k≤xmax

umin≤ut+k≤umax

xt|t=x(t)

式中：xt+k|t为在时间(t+k)处的预测状态向量；ut+k为在时间(t+k)处的信号控制序列，从状态x(t)开始，通过将输入序列ut,…,ut+k-1应用在式(6)中得出预测状态向量；UN为在控制周期内的最优信号控制序列；xmax为各个路段的最大车辆容纳量；umin,umax分别为相应路口最小绿灯时间和最大绿灯时间；Q和R是对角非负正定矩阵，Q为道路中最大车辆数的状态矩阵，对角线元素等于1/(xmax)2，矩阵R通常定义为R=rI，其中r可通过实验得出。

2.2　EMPC的离线计算

多参数规划技术通常应用在由目标函数、一组参数向量和一组约束组成的优化问题中。优化变量的最优值通过优化变量和相应状态参数区域之间的显式表达式计算。作为通用数学技术，可以使用多参数规划方法来获得优化变量U关于状态参数x(t)的函数。EMPC通过多参数规划方法划分交通流的状态空间并获得相应分区的最优控制规律，则传统的MPC系统可以转换为分段仿射(PWA)系统。因此，可以离线获得最优信号配时控制律的显式表达，从而不需要重复地在线优化。

状态更新方程替换为如下形式：

(8)

则优化模型可以转化为如下形式：

s.t.GU≤W+Sx(t)

(9)

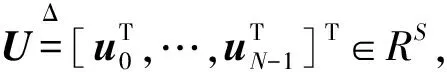
U*(x(t))=Fix(t)+Gix(t)∈CRi

(10)

式中CRi=[x∈Rn|Lix≤Ki]，其代表临界区，是参数空间φ={x∈Rn|Lx≤K}的凸分区。通过多参数规划方法可以求得参数L，Li，K，Ki，Fi，Gi。EMPC系统可以分为两部分，即离线计算和在线计算，对于离线计算，通过应用多参数规划技术凸划分交通流状态空间，并且可以获得相应分区的最优信号控制律。对于每个CRi，最优信号控制律是其对应状态的线性函数。

2.3　EMPC的在线查找

EMPC的在线计算过程是通过搜索状态分区表CRi={x∈Rn|Lix≤Ki}来确定当前交通状态所属的状态区域CRi，即x(t)∈CRi。然后，直接获取相应的交通状态区域CRi的信号控制规律，即u(t)=fix(t)+gi。因此，执行线性搜索以定位当前交通状态x(t)的状态空间，然后查找相应的反馈增益(Fi,Gi),是在线阶段的主要工作。当找到当前交通状态的对应区域时，信号控制量可以根据式(10)计算。

线性顺序查找方法用于搜索整个状态区域以确定当前状态点是否位于某一个区域，直到找到位于x(t)的状态区域。如果没有找到状态区域，则使用最近可行区域的信号控制规律代替。

3　仿真实验结果分析与讨论

考虑到成本和交通安全，实际交通系统不可能随时更改新的信号配时方案。因此，本文的仿真实验是在一种广泛使用的交通模拟软件Paramics上进行的，通过控制如图2所示区域交通路网来验证使用EMPC进行信号控制的效果。字母A～F表示6个交叉路口，1～13表示13个单向链路组成。此外，根据Paramics的要求，特别设定了7个特殊的矩形框，表示流入和流出，例如Sin,1和Sout,1。路网中路段的容量均设置为100辆。左转弯率、直行率和右转弯率分别被设置为30%、40%和30%。每个信号周期的时长设置为55s，每个交叉路口在控制周期内至少包含两个相位，绿灯时间的最大值和最小值分别为50s和5s。路口的饱和流率均设置为1 900辆/h。仿真过程中的控制步长为0.5s，整个仿真为32个周期共1 760s，车辆以1 200辆/h的流率进入路网。

图2　仿真实验交通路网图

本文所有的仿真实验都在配置为32G内存、3.5GHz CPU、Windows7操作系统的Dell工作站上进行。实验选用MATLAB和C++为编程语言，采用Paramics交通仿真软件进行仿真，使用MATLAB生成EMPC控制器，使用C++语言生成Paramics仿真所需的显式控制率。仿真结果的比较分别从可行性和效率两方面进行。

3.1　基于EMPC的信号控制器的可行性

为了证明可行性，将基于EMPC的信号控制器的控制性能与固定时间控制(fixed-time control，FTC)策略进行比较，对于总时间消耗(total time spent, TTS)和总车辆出发(total vehicle departure, TVD)进行评估。图3是两种方法的TTS指标的对比图，从图可以很明显看出，基于EMPC的方法相对于定时长方法具有更大的优势。TVD指标反映的是有多少车辆离开区域交通路网，该指标的价值在于评价两种方法缓解交通拥堵的能力，实验结果如图4所示，其中横轴表示与控制时间同步的模拟时间，纵轴表示每个控制周期的累积离开的车辆数，从图可以看出，基于EMPC方法的TVD指标高于FTC方法。实验所得到的TTS和TVD的数据是在相同设置下的10次模拟实验的平均值，实验结果表明基于EMPC的方法可以应用于信号控制。

图3　基于EMPC方法与基于定时长方法的TTS对比图

图4　基于EMPC方法与基于定时长方法的TVD对比图

为了避免实验结果的随机性，在仿真实验中，随机选择了路网中的3条路段，测试了这3条路段中不同时间节点中车辆数量的变化情况，如图5所示。实验结果直观地表明，在基于EMPC的方法中3条不同路段的车辆数量总体上明显小于固定时长信号控制方法，说明在该方法的控制下，道路的通行能力得到提升，更加明确地表明了EMPC法相较于FTC更能及时有效地缓解交通拥堵问题。

图5　基于EMPC方法与基于定时长方法在不同路段上车辆数的对比图

3.2　基于EMPC的信号控制器的有效性

为了满足实时要求，优化控制效率对于信号控制器来说十分重要。如前所述，在线计算的高复杂度是MPC的主要缺点，而基于EMPC的方法旨在克服这个缺点。为了评估EMPC控制器的效率，进行了10次实验，得出的最终结果是这10个结果的平均值。图6显示了EMPC控制器和MPC控制器所消耗的CPU时间。两种算法的CPU用时均随着路段数量的增加而增加，与MPC控制器相比，EMPC占用CPU时间仅为0.5～1.5s。仿真实验结果显示，两种方法的整体计算时间都会随着路网中路段数量的增加而增加，但EMPC的CPU使用时间和增长速率明显地低于MPC方法。

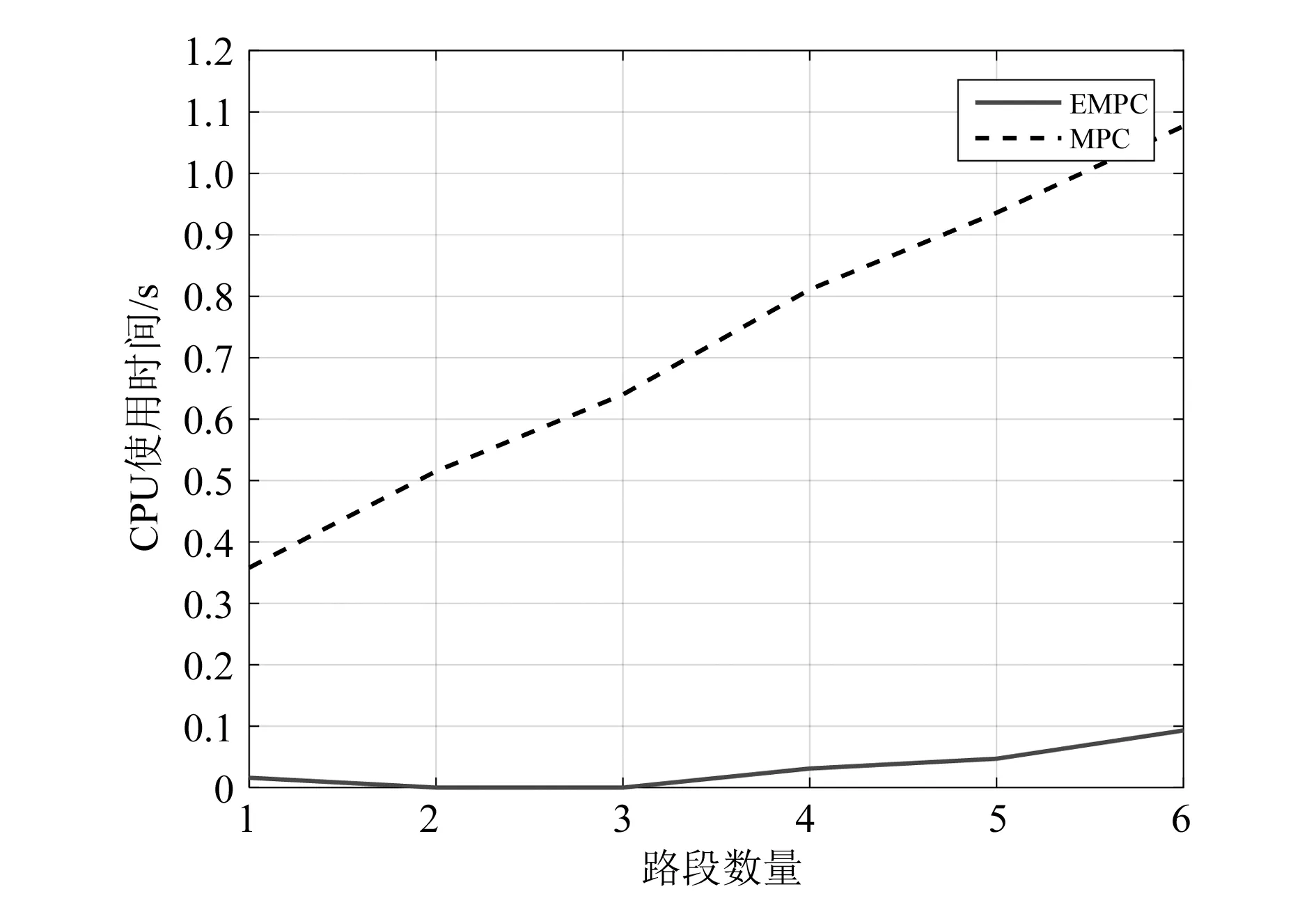
图6　基于EMPC方法与基于MPC方法的CPU用时对比图

4　结束语

本文结合存储转发模型和线性二次最优控制理论，构建带约束的交通控制信号优化模型，同时将显式模型预测控制引入大型交通路网的交通信号控制问题中。通过将传统MPC的在线优化过程转变为在线查表过程，交通控制信号的优化可以通过快速离线计算得到每个对应状态分区上的状态反馈最优显式控制律。结合仿真实验结果可知，基于EMPC的交通信号控制方法考虑到交通流的实时性需求，将离线计算与在线计算有效结合，通过与固定时长信号控制策略比较验证了基于EMPC控制器的实时可行性。同时，为了克服传统模型预测控制在线计算量的问题，显式模型预测控制通过引入多参数规划方法巧妙地提升了预测控制的控制效率，并通过实验比较了两种方法的CPU耗时，验证了EMPC方法在交通信号配时优化问题中的控制性能。

参考文献:

[1]PAPAGEORGIOU M. Overview of road traffic control strategies[J]. IFAC Proceedings Volumes, 2004, 37(19):29-40.

[2]ABOUDOLAS K, PAPAGEORGIOU M, KOSMATOPOULOS E. Store-and-forward based methods for the signal control problem in large-scale congested urban road networks[J]. Transportation Research Part C Emerging Technologies, 2009, 17(2):163-174.

[3]XIE X F, SMITH S F, LU L, et al. Schedule-driven intersection control[J]. Transportation Research Part C Emerging Technologies, 2012, 24(1):168-189.

[4]ZHU F, UKKUSURI S V. A linear programming formulation for autonomous intersection control within a dynamic traffic assignment and connected vehicle environment[J]. Transportation Research Part C Emerging Technologies, 2015, 55:363-378.

[5]RAMEZANI M, HADDAD J, GEROLIMINIS N. Dynamics of heterogeneity in urban networks: aggregated traffic modeling and hierarchical control[J]. Transportation Research Part B, 2015, 74:1-19.

[6]BRETHERTON D, BODGER M, BABER N. SCOOT-the future urban traffic control[C]//IEE International Conference on Road Transport Information and Control.London, UK：IET,2004:301-306.

[7]SIMS A G. SCAT, the sydney co-ordinated adaptive traffic system[J]. IEEE Transactions on Vehicular Technology, 1981, 29(2):130-137.

[8]GARTNER N H. OPAC: ademand responsive strategy for traffic signal control[J]. Transportation Research Record Journal of the Transportation Research Board, 1983, 906:75-81.

[9]SEN S, HEAD K L. Controlled optimization of phases at an intersection[J]. Transportation Science, 1997, 31(1):5-17.

[10] XI Y G, LI D W, LIN S. Model predictive control——status and challenges[J]. Acta Automatica Sinica, 2013, 39(3):222-236.

[11] ABOUDOLAS K, PAPAGEORGIOU M, KOUVELAS A, et al. A rolling-horizon quadratic-programming approach to the signal control problem in large-scale congested urban road networks[J]. Transportation Research Part C Emerging Technologies, 2010, 18(5):680-694.

[12] LIN S, SCHUTTER B D, XI Y G, et al. Efficient network-wide model-based predictive control for urban traffic networks[J]. Transportation Research Part C Emerging Technologies, 2012, 24(9):122-140.

[13] LIN S, SCHUTTER B D, XI Y G, et al. Fast model predictive control for urban road networks via MILP[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(3):846-856.

[14] ZHOU Z, SCHUTTER B D, LIN S, et al. Two-level hierarchical model-based predictive control for large-scale urban traffic networks[J]. IEEE Transactions on Control Systems Technology, 2017, 99:1-13.

[15] NEGENBORN R R, SCHUTTER B D, HELLENDOORN J. Multi-agent model predictive control for transportation networks: Serial versus parallel schemes[J]. Engineering Applications of Artificial Intelligence, 2008, 21(3):353-366.

[16] OLIVEIRA L B D, CAMPONOGARA E. Multi-agent model predictive control of signaling split in urban traffic networks[J]. Transportation Research Part C Emerging Technologies, 2010, 18(1):120-139.

[17] ZHOU Z, SCHUTTER B D, LIN S, et al. Multi-agent model-based predictive control for large-scale urban traffic networks using a serial scheme[J]. IET Control Theory & Applications, 2015, 9(3):475-484.

[18] ZHANG J, WANG W. Synthesis of explicit model predictive control system with feasible region shrinking[C]//Wseas International Conference on Robotics, Control and Manufacturing Technology.Hangzhou：WSEAS, 2008:80-85.

[19] BEMPORAD A, MORARI M, DUA V, et al. The explicit linear quadratic regulator for constrained systems[J]. Automatica, 2002, 38(1):3-20.

[20] ZHANG J, CHENG X, ZHU J. Control of a laboratory 3-DOF helicopter: Explicit model predictive approach[J]. International Journal of Control Automation & Systems, 2016, 14(2):389-399.

[21] OBERDIECK R, DIANGELAKIS N A, PISTIKOPOULOS E N. Explicit model predictive control: a connected-graph approach[J]. Automatica, 2017, 76:103-112.

[22] TØNDEL P, JOHANSENT A, BEMPORAD A. An algorithm for multi-parametric quadratic programming and explicit mpcsolutions[J]. Automatica, 2002,39(3):489-497.

[23] DIANGELAKIS N A, AVRAAMIDOU S, PISTIKOPOULOS E N. Decentralized multiparametricmodel predictive control for domestic combined heat and power systems[J]. Industrial & Engineering Chemistry Research, 2016, 55(12):3313-3326.

[24] ALLEN M, ASTLE B, BURT J. Model predictive control based on linear programming-the explicit solution[J]. IEEE Transactions on Automatic Control, 2002,47(12):1974-1985.

[25] BEMPORAD A. A multiparametricquadratic programming algorithm with polyhedral computations based on nonnegative least squares[J]. IEEE Transactions on Automatic Control, 2015, 60(11):2892-2903.