TB轮胎自动修边机侧刀组件设计及位置分析

鲁健武，杨超君，袁　浩，虞　鹏

(江苏大学机械工程学院，江苏 镇江　212013)

轮胎的一般加工工序为：密炼—胶部件准备—轮胎成型—硫化—检验—测试[1]。硫化时由于考虑到排气的问题，因此需要在活络模中设计气孔，这样就会产生胎毛[2]。传统的手工轮胎修边机修剪胎毛时手工操作多、劳动强度大、生产效率低、产品质量不稳定，还会影响操作工人的身体健康。采用轮胎自动修边机，能有效解决上述问题[3]。

目前市场上有不少修边机产品，但存在不能全部去除轮胎侧面胎毛的问题，特别是内圈的胎毛，主要原因是刀片下刀初始位置不准确。分析其原因：1)轮胎侧面曲线是不规则的；2)轮胎侧面印有各种参数和信息，凹凸不平；3)修边刀具很难与胎面紧密贴合；4)刀具对胎面的压力很难均匀控制。由于轮胎侧面客观存在的各种复杂因素，因此胎侧胎毛的去除是整个修边过程中的难点，故而合理安放刀具成为保证修边效果的前提。

本文研究的重点是基于参数化的轮胎尺寸，得出修边机侧刀机构中各构件之间的参数化位置关系，通过理论分析及机构运动仿真分析来确定刀具合适的初始位置，从而提高修边效果[4]。

1　侧刀部件工作情况分析

图1是一种全自动轮胎修边机的侧刀加工原理图，图中1是上部刀具，2是待修边轮胎，侧刀组件由分别置于轮胎两侧的侧刀部件3-1及3-1′、侧刀部件移动机构3-2和3-5、水平移动驱动电机3-3、轮胎旋转辊轮4和4′、轮胎旋转驱动电机3-4、竖直移动驱动电机3-6组成。

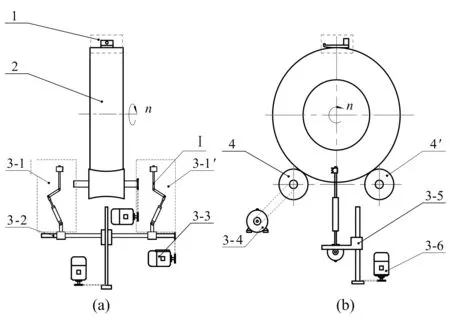
图1　全自动轮胎修边机侧刀部件原理图

工作流程：待修边轮胎进入修边位置，轮胎在辊轮的驱动下匀速旋转，侧刀部件在移动机构的作用下开始向轮胎左右两侧及向上进给，到达某一合适位置后停止，此时修边刀具在执行气缸的作用下顶在轮胎侧面，侧刀组件在移动机构的作用下整体向下匀速运动，直至修边完成。

2　侧刀部件结构及其机构简化

侧刀部件3-1及3-1′中刀具机构简化图如图2所示。刀具机构由以下几个零件组成：1)刀头；2)刀座；3)摆动杆1；4)连接轴；5)摆动杆2；6)气缸；7)气缸支座。刀头与刀座通过销轴连接，可以转动；刀座上的孔套在摆动杆1上，可以转动与滑动；摆动杆1与摆动杆2都是固定在连接轴上并通过螺钉锁紧，保证没有相对位移，但是可以通过螺钉改变其相对夹角；摆动杆2与气缸通过浮动接头连接，可以转动。图2可以清楚地反映出各构件的运动关系。

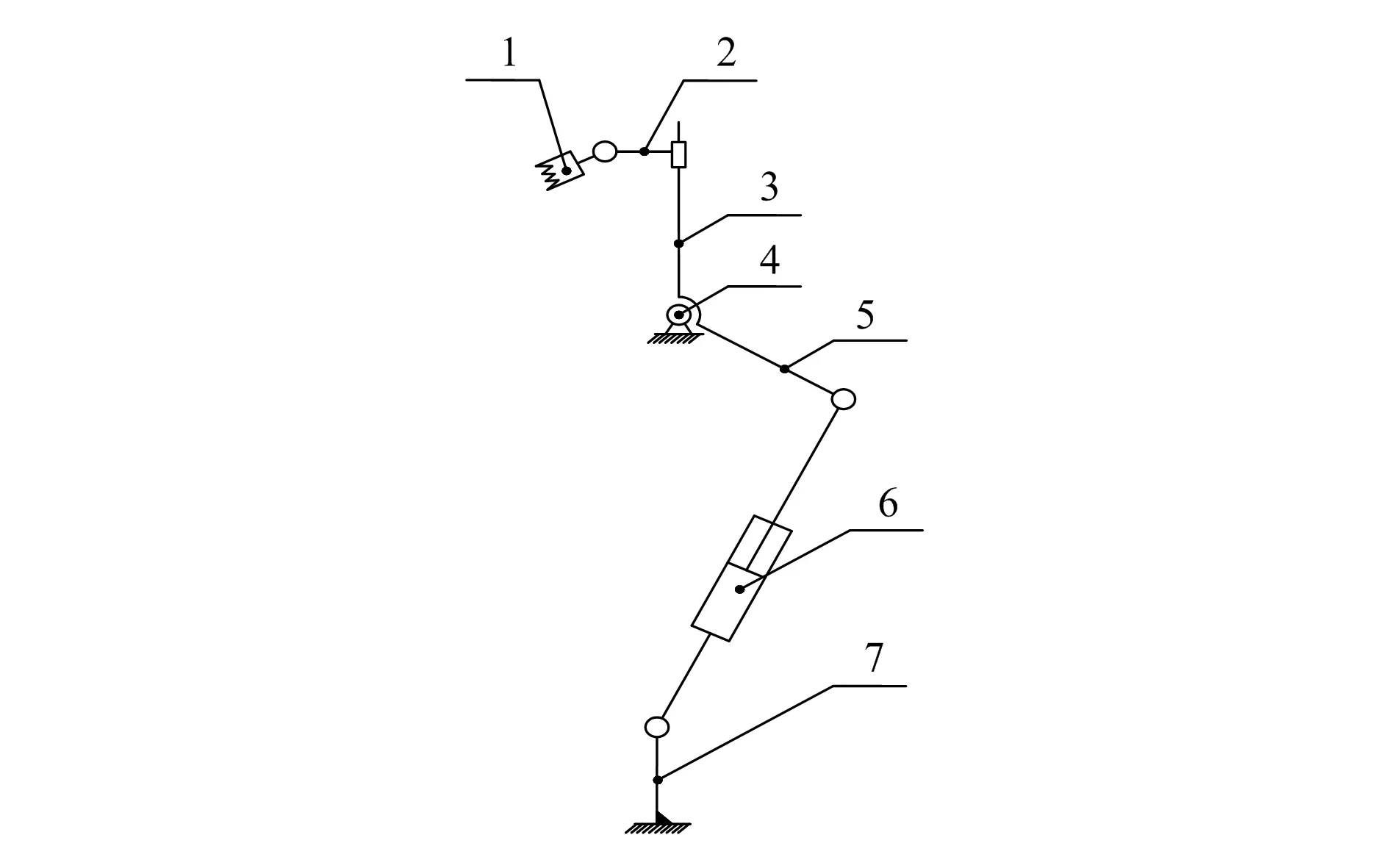
图2　单个修边刀具机构

为了分析上述修边刀具机构的运动情况，选择空间机构合适的坐标系。图1中，以两辊轮连线与轮胎竖直方向中心线的交点作为全局坐标系{O}的原点，为了方便后面的计算，根据图2简化的刀具机构示意图，将图1简化成图3。

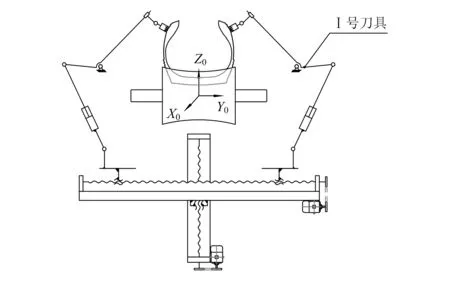
图3　侧刀组件简化图

3　侧刀组件运动学分析

3.1　机构运动学理论基础

空间机构的运动学分析有很多种方法，齐次变换是其中比较直观、方便的一种[5]。根据D-H法中通行的坐标系建立原则，标记相邻两坐标系(i-1)与i系，则相邻两坐标系的变换矩阵为[6]：

(1)

式中：cθi=cosθi,sθi=sinθi；Rx(αi-1)表示(i-1)坐标系绕x轴旋转αi-1角度；Dx(αi-1)表示(i-1)坐标系沿x轴移动ai-1距离；Rz(θi),Dz(di)以此类推。

3.2　轮胎轮廓曲线方程

图4是具有带束层和加强层约束的子午线轮胎断面轮廓曲线，横坐标y是轮胎断面宽度，纵坐标r是轮胎断面至旋转轴的距离，rm为轮胎最宽点至旋转轴的半径，re为加强层上端至旋转轴的半径，rb为胎圈中心至旋转轴的半径，rk为胎冠点至旋转轴的半径，rd为带束层端点至旋转轴的半径，轮胎外轮廓相对中心的距离(rb≤r≤rd)计算公式[7]为：

(2)

式中：ym为轮胎端面宽度；ζ=1-g，g为压力分担率。

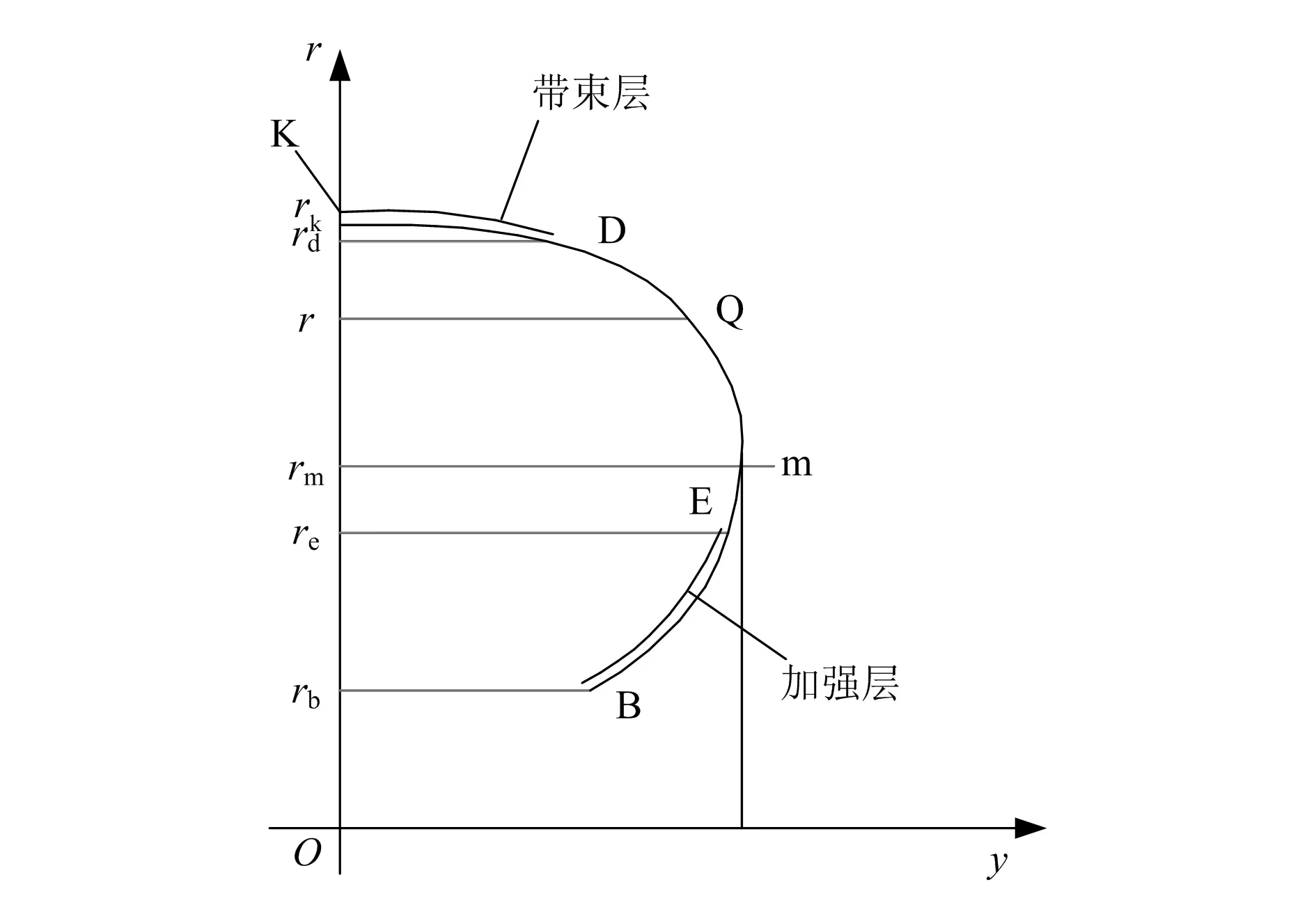
图4　子午线轮胎断面轮廓曲线

由式(2)可得任意部位轮廓曲线位置参数，为刀具刀头在轮胎上位置的合理控制提供依据。

3.3　侧刀组件位置分析

3.3.1侧刀组件运动分析正解

为了达到理想的修边效果，必须确定侧刀各个部件在空间的相对位置，特别是侧刀部件中刀具的位置。为了计算刀具合适的空间位置，首先在图3的基础上得到侧刀组件的运动简图(如图5所示)，然后对Ⅰ号刀具进行位置分析。

1)根据D-H坐标系建立图5中各杆的坐标系。

如图5所示，L为轮胎旋转中心距全局坐标系{O}YZ轴平面的垂直距离；R为轮胎最大半径；d1为竖直滚珠丝杠距全局坐标系{O}YZ轴平面竖直移动的距离；d2为水平滚珠丝杠距全局坐标系{O}YZ轴平面水平移动的距离；d3为刀头距旋转中心移动的距离；l=451mm；θ1=71°。

图5　侧刀组件运动简图

2)确定连杆的D-H参数和关节变量[8]。

根据3.1机构运动学理论基础中关于连杆参数定义的方法，可以得出侧刀组件的D-H参数见表1。

表1　侧刀组件的D-H参数表

将表1中的D-H参数代入式(1)得相邻两坐标系的变换矩阵：

式中：θ2为刀头围绕转动轴转动的角度。

4)求刀头在全局坐标系中的坐标[9]。

(3)

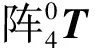
(4)

式(4)明确了刀具在全局坐标系中的位置，从而使得刀具能与轮胎的确定位置相贴合。

3.3.2刀头运动方程正确性验证

1)刀头运动轨迹离散化求解。

通过式(4)可以得出刀头在全局坐标系三个坐标轴方向的位移分别为：

Wx=0

Wy=-75sθ2+d3cθ2+d2+lcθ1

Wz=75cθ2+d3sθ2-d1+lsθ1

(5)

为了下文计算与验证的方便，假设每个移动副与转动副同时运动、同时结束，且每个运动关节的运动都是匀速运动。下面设置各个运动关节的速度与运动时间t(s)，v1,v2,v3分别为每个移动副的运动速度(m/s)，ω2为转动副的转动角速度(rad/s)。

d1=v1t，v1=21.2；

d2=v2t，v2=13.0；

d3=v3t，v3=17.0；

θ2=ω2t+π/2，ω2=π/30；

t∈[0,10]。

将上述各参数代入式(5)，并利用MATLAB编程，得到刀头在全局坐标系3个坐标轴方向的位移以及总位移[10],如图6所示。

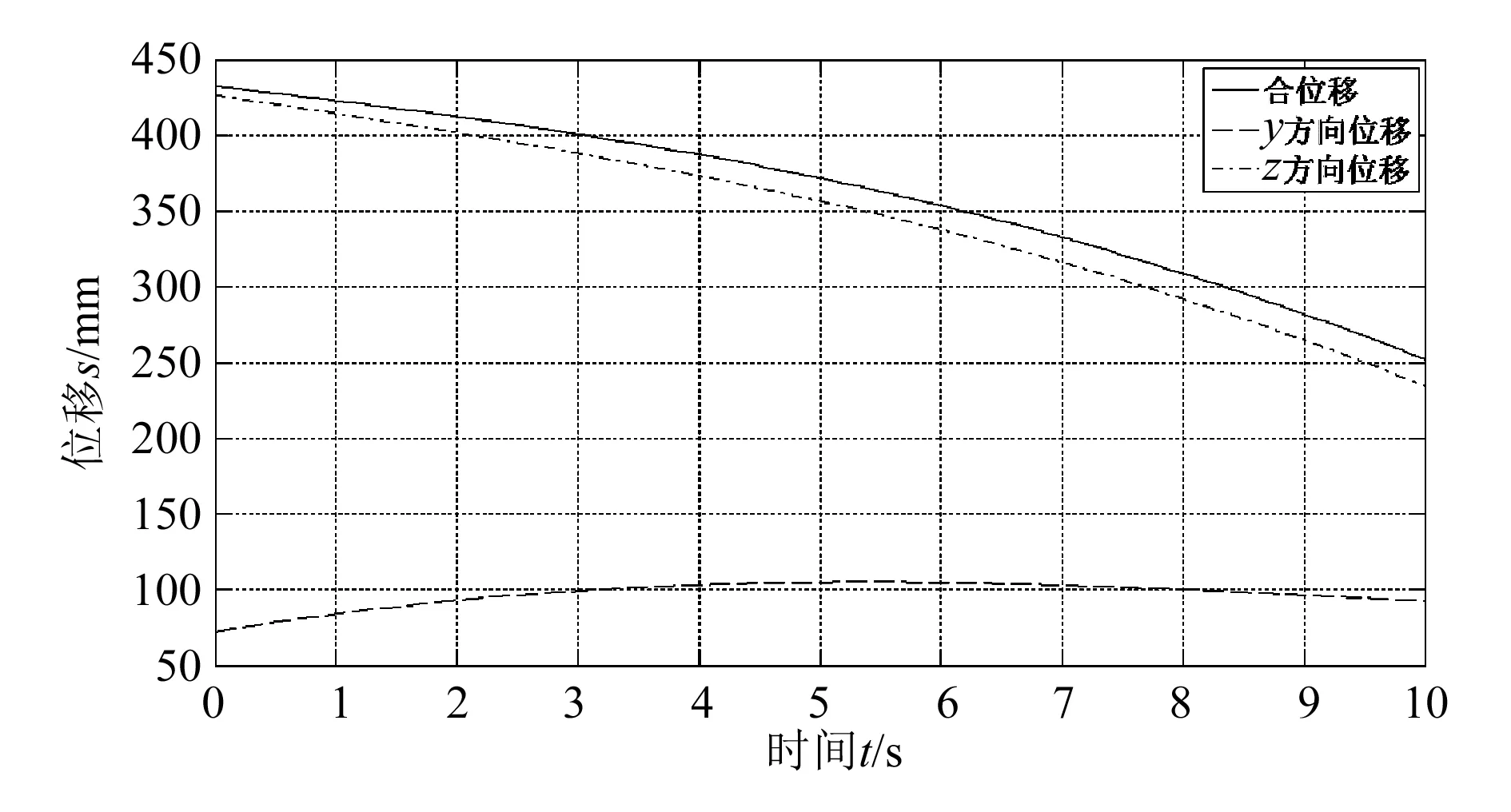
图6　理论位移曲线

2) 刀头运动学仿真。

利用Pro/E5.0绘制刀具的三维模型图如图7所示，并且利用其自带的机构分析模块对刀具进行运动学仿真，得出刀头的位移曲线如图8所示。

图7　刀具的三维模型

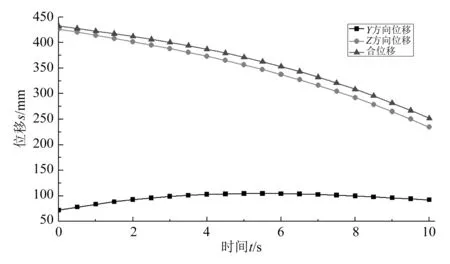
图8　仿真位移曲线

3) 结果分析。

如图6和8所示，理论位移曲线与仿真位移曲线中各分位移、合位移的走势都一致且吻合性很好，从而可以验证运动方程的正确性，进而验证侧刀部件运动的可行性。

3.3.3侧刀组件运动分析反解

若末端连杆的位姿已经给定，由图5可知，当刀具上点P到达修边部位P1时，此时刀具在空间的位姿参数n,o,a,p为已知，据此求出各运动关节的运动参数θ2,d1,d2,d3的值称为运动反解。用未知的连杆逆变换左乘式(3)两边，把关节变量分离出来，从而求解。图5中，r=rb+35(因为修边刀片宽度的原因，这个是距离轮胎边缘的合适距离)，根据胎侧部位(rb≤r≤rd)的计算公式(2)，可以求得坐标位置y(r)。子午线轮胎断面轮廓曲线与实际的轮胎外形尺寸还有一个轮胎胶料厚度的差别，因此在y(r)的基础上要加上胶料厚度h，这样末端刀片的位置P1(0,y(r)+h,L-r)就确定了。接下来确定末端刀片的姿态，为了达到相对理想的修边效果，要求刀片与胎侧最好达到近似垂直的状态，但是为了计算有普适性且可以参数化，设计垂直于刀片的轴线通过(0,0,rm)点，这样就可以确定末端刀片的姿态角α，见式(6)：

(6)

在末端刀片的空间位置以及空间姿态已经确定的情况下，其位姿矩阵为：

(7)

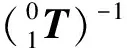
(8)

令式(8)两端的元素(2,1)、(2,2)、(2,4)、(3,4)对应相等，再根据式(6)可得：

(9)

从式(9)可以看出，自变量只有d3，因变量是θ2,d1,d2，当确定了d3时其他参数也就确定了，说明当修边机工作时，只要改变1个参数就可以将刀头调整到初始修边位置且可以很好地贴合胎面，大大缩短了机器的调试时间，提高了工作效率。

4　结束语

基于轮胎生产工艺的限制，轮胎的胎面与胎侧会产生胎毛，轮胎修边机的侧刀组件可用于去除胎侧胎毛。本文通过对轮胎自动修边机中侧刀机构的简化，可以直观了解机器的修边动作以及方便机构计算，利用MATLAB数值分析和Pro/E5.0的运动仿真验证运动方程的正确性，进而验证侧刀部件运动的可行性，通过对侧刀组件的运动学反解得出侧刀部件中各机构的运动关系，使得刀头可以精确贴合在不同型号的轮胎上，保证了刀片对胎毛的完全去除，提高了轮胎的修边质量。

参考文献：

[1]林礼贵.轮胎生产工艺[M].北京：化学工业出版社,2008:56-58.

[2]翁国文.橡胶硫化[M].北京：化学工业出版社,2005:45-49.

[3]江维华.车辆轮胎修边机：201020566465.0 [P].2011-06-08.

[4]于喜红,白晶,张顺琦,等.开放式四自由度工业机器人控制系统研究[J].机械设计与制造工程,2015,44(8):39-40.

[5]张铁，谢存禧.机器人学[M].广东：华南理工大学出版社，2001:59.

[6]克莱格.机器人学导论[M].3版. 贠超,译.北京：机械工业出版社，2006：49-54.

[7]王国林,万治君，梁晨，等.基于非平衡轮廓理论的子午线轮胎结构设计[J].机械工程学报,2012,48(24):112-118.

[8]崔文,李成刚,林家庆,等.柔性关节机器人的凯恩动力学建模与仿真分析[J].机械设计与制造工程,2015,44(12):5-7.

[9]蔡自兴.机器人学基础[M].2版.北京：机械工业出版社，2015:43-47.

[10] 张采芳,余愿,鲁艳旻.MATLAB编程及仿真应用[M].武汉:华中科技大学出版社,2014.