肉用西门塔尔牛群体生长曲线拟合及体重与体尺相关性分析的研究
2018-04-04梁永虎金生云宝金山徐凌洋张路培高会江李俊雅
梁永虎,朱 波,金生云,宝金山,徐凌洋,陈 燕,高 雪,张路培,高会江,李俊雅*
(1.中国农业科学院北京畜牧兽医研究所,北京 100193; 2.锡林郭勒盟乌拉盖管理区兽医局,乌拉盖 026321)
西门塔尔牛早在20世纪初作为兼用品种引入我国[1],主要用于改良我国黄牛,其杂交后代大约占我国杂交改良牛的50%[2]。由于其良好的生产性能[3],育种工作者对其进行了大量的基础性研究工作。H.Z.Fan等[4-8]利用全基因组关联分析方法对肉用西门塔尔牛群体的肉质性状和生长性状进行了初步研究。B.Zhu等[8-9]首次系统地评估了肉用西门塔尔牛群体的生长发育、胴体和肉质性状的基因组育种值估计的准确性,为我国肉牛全基因组选择研究提供理论基础。牛红等[10]采用非求导约束最大似然法估计遗传力、遗传相关和方差组分对肉用西门塔尔牛群体的重要经济性状进行了遗传参数和方差组分估计,为将来制定育种方案和遗传评估奠定基础。
畜禽生长曲线拟合是研究和分析畜禽生长发育规律的重要方法之一,鉴于动物生长的非线性特性,可以通过几个非线性生物学参数描述动物的生长发育规律,即生长曲线模型。Logistic、Brody、Gompertz和Bertallanffy等4种模型是常用的用于描述畜禽生长规律的非线性数学模型,不仅对畜禽生长曲线拟合效果好,而且其中的参数估计值都能够反映不同种群在生长率和最大体重方面的差异[11-12]。该模型在指导牛的育种、确定适配年龄和屠宰年龄及控制生长发育上均起到了重要作用。国外许多肉牛品种,如海福特牛和安格斯牛的生长曲线均已建立[13-14],国内秦川牛、延边牛和安西牛等品种的生长曲线方程也已建立[15-18]。马光辉等[19]应用Wood不完全伽玛函数模型、Nelder逆多项式模型和Wilmink模型等3个数学模型,分别对新疆呼图壁种公牛场肉用西门塔尔牛第一胎、第二胎、第三胎、
第四胎、四胎及以上所有胎次的泌乳曲线进行了拟合,通过SAS统计软件进行分析,发现Wood模型的拟合度最好,拟合效果最优。而关于肉用西门塔尔牛群体的生长曲线尚未见报道。
本研究通过对内蒙古乌拉盖地区肉用西门塔尔牛群体的体重、体高、体斜长、十字部高、胸围和腹围等指标数据进行分析,研究其生长发育规律并揭示各性状间的相互关系,同时肉用西门塔尔牛体重的预测方程可为实际的体重测量提供参考依据。
1 材料与方法
1.1 数据来源
本研究所采用数据来自于中国农业科学院北京畜牧兽医研究所牛遗传育种创新团队。该团队从2008年开始构建肉用西门塔尔牛资源群体,该资源群体位于内蒙古锡林郭勒盟乌拉盖管理区,经过逐年扩群,至2016年肉用西门塔尔牛群体基础母牛已超过2 000头,资源群体的父亲来自于39头肉用西门塔尔牛种公牛。每年7~8月份,测定该群体犊牛的生长发育性状,包括体重和体尺性状。为了便于数据测量,每年10月份将乌拉盖地区5~9月龄的肉用西门塔尔牛运送到北京金维福仁清真食品有限公司,并按照统一的饲养管理方法进行集中育肥,在集中育肥过程中,每3个月需测量一次体重和体尺数据。
1.2 拟合生长曲线模型
分别选择Logistic、Brody、Gompertz和Bertallanffy 4种生长曲线模型拟合其生长曲线(表1),根据曲线方程可反映出生长发育规律的曲线拐点体重及达到拐点体重的拐点月龄等指标[20]。
表1生长曲线模型及特征
Table1Growthcurvemodelsandcharacteristics

生长曲线模型Growthcurvemodel公式Formula拐点体重/kgInflectionpointweight拐点月龄Inflectionpointmonth相对生长率Therelativegrowthrate最大日增重/kgThebiggestdailygainLogisticY=A/(1+Be(-kt))A/2(LnB)/kk(1-wi/A)kw/2GompertzY=A×e-B×exp(-kt)A/e(LnB)/kk(lnA-lnwi)kwBertallanffyY=A×(1-B×e-kt)38A/27(Ln3B)/k3k((A/wi)1/3-1)3kw/2BrodyY=A×(1-B×e-kt)__k((A/wi)-1)kw/2
方程中,A为成熟体重或体尺,B为常数尺度,k为顺势相对生长率,wi为观测值体重,t为生长时间,e为自然对数
Ais mature body weight or body measurements,Bis constant scale,kis the relative growth rate,wiis observed weight,tis the growth time,eis the natural logarithm in equations
R2是用来评价拟合曲线方程优劣的指标,即拟合度:
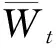
1.3 统计分析
使用SAS 9.4软件中的NLIN过程对整理后的数据进行曲线模型方程参数的最优估计[21],采用Gauss-Newton法进行环迭代来估计参数使残差平方和最小,收敛标准为10-8。同时对肉用西门塔尔牛体尺及体重进行相关性分析,以及利用体尺性状对体重进行回归分析,获得对肉用西门塔尔牛体重的回归预测方程。采用于志等[22]对中国荷斯坦牛育成牛生长发育规律的相关分析方法,计算公式:
Y=ba+b1X1+b2X2+b3X3+b4X4+b5X5
公式中,Y为体重,X1为体高,X2为十字部高,X3为体斜长,X4为胸围,X5为腹围,ba为常数,b1、b2、b3、b4、b5为回归系数。
相关系数r根据Pearson公式进行分析,计算模型:
上式中,i=1,2,3,4,5,N为试验牛头数,X1、X2、X3、X4、X5同上,Y为体重。
2 结 果
2.1 肉用西门塔尔牛不同月龄体尺体重统计结果
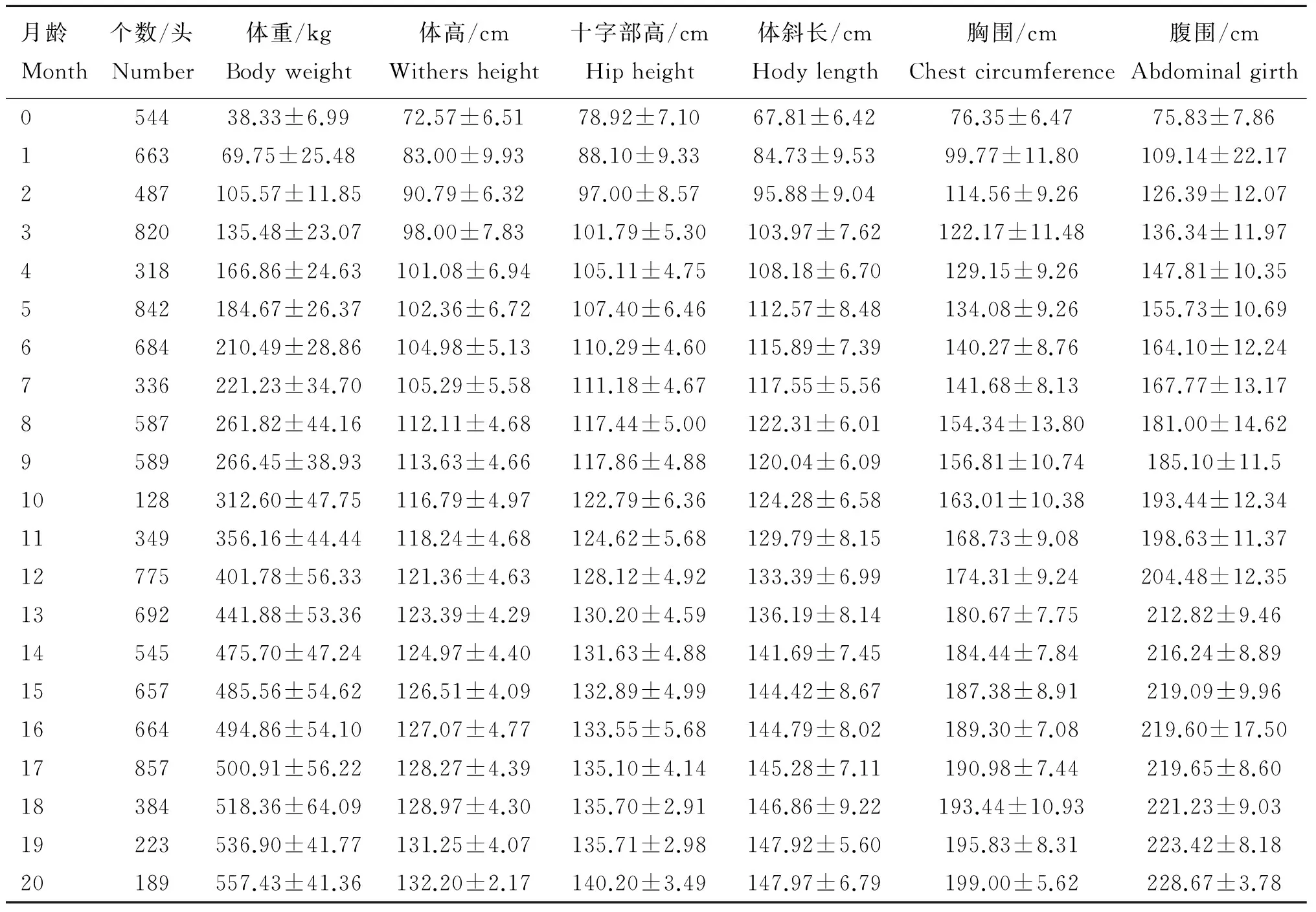
如表2 所示,肉用西门塔尔牛从出生到20月龄体重、体尺平均值呈逐增态势,但各阶段增幅不一,体重自出生到12月龄增幅较大,13~20月龄增幅缓慢。对于体高、体斜长、十字部高、胸围和腹围均是在出生到6月龄增速最快,之后增速缓慢,15~20月龄增幅最小。从标准误可以看出,随着月龄的增加,肉用西门塔尔牛个体间的体尺波动较小。而体重是由出生最小的标准误6.99逐渐增加到18月龄的64.09,个体间的差异较大。
2.2 肉用西门塔尔牛4种数学模型各参数估计值
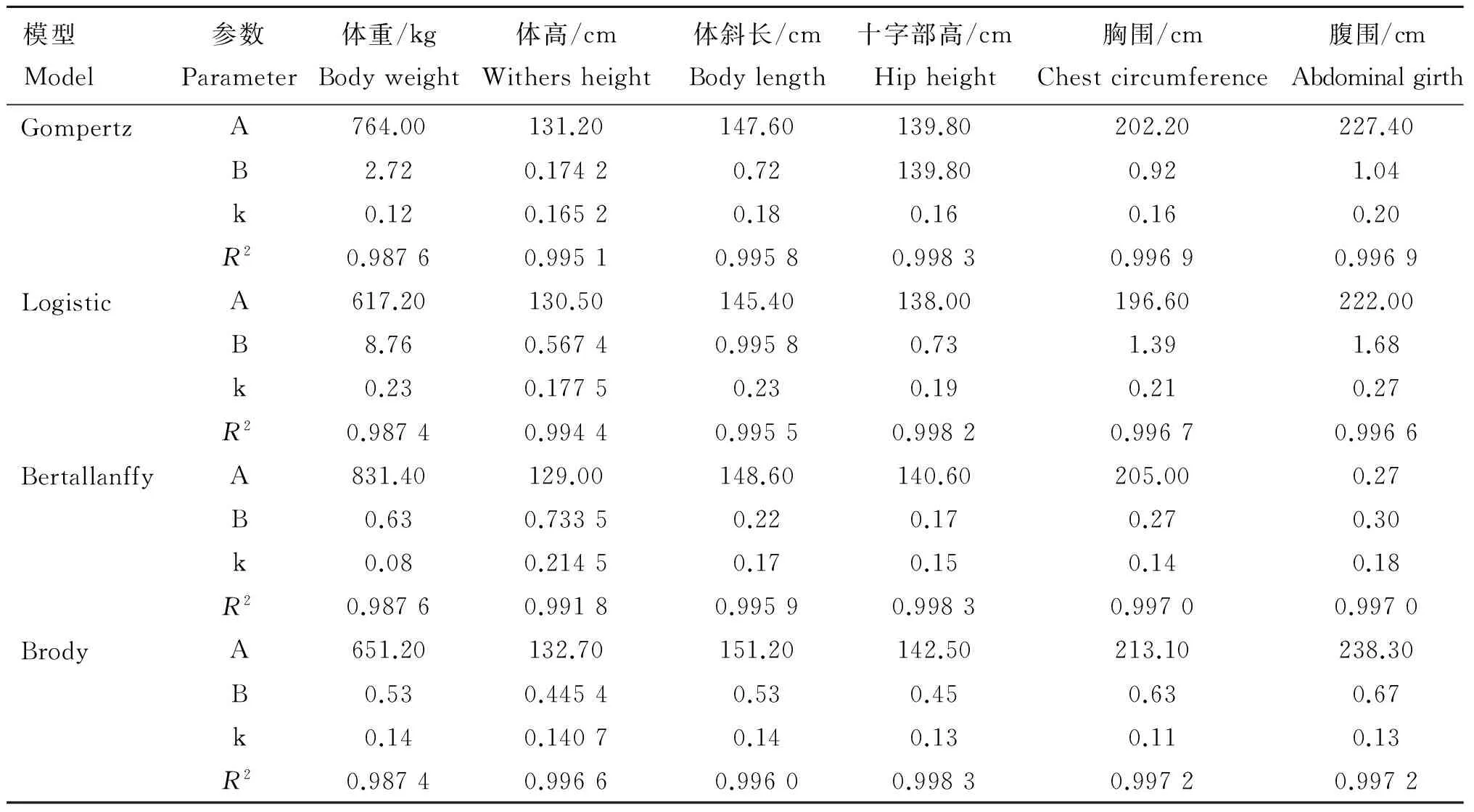
通过SAS 9.4运行结果汇总4种模型的参数估计值如表3所示,可以看出4种模型都能很好拟合肉用西门塔尔牛的各项指标,除体重外其他各项拟合度均在0.99以上。Bertallanffy模型在20月龄时最大体重可达831.40 kg, 而Logistic模型在20月龄是仅为617.20 kg, Gompertzhe模型和 Brody模型则分别为764.00 kg和651.20 kg,处于前两者之间。但顺势相对生长率最大的Logistic模型较最小的Bertallanffy模型高0.15。
生长曲线拐点是反映动物生长率最大的时间点,Gompertz和Bertallanff生长曲线模型的拐点是固定的,如表4所示,其中Logistic模型在9.46月龄时到达拐点,体重为308.55 kg,最大日增重为1.140 kg,对于模型Gompertz,生长至8.47月龄时,最大日增重是1.051 kg,随后逐渐下降,此时体重为281.81 kg。Bertallanff模型的最大日增重最小1.007 kg,在7.15月龄时,体重达到268.62 kg。因为Brody模型的拐点月龄和体重是不稳定的,所以不存在相关参数值。
表2肉用西门塔尔牛体尺、体重统计结果
Table2ThestatisticsofbodymeasurementsandbodyweightofSimmentalbeefcattle
月龄Month个数/头Number体重/kgBodyweight体高/cmWithersheight十字部高/cmHipheight体斜长/cmHodylength胸围/cmChestcircumference腹围/cmAbdominalgirth054438.33±6.9972.57±6.5178.92±7.1067.81±6.4276.35±6.4775.83±7.86166369.75±25.4883.00±9.9388.10±9.3384.73±9.5399.77±11.80109.14±22.172487105.57±11.8590.79±6.3297.00±8.5795.88±9.04114.56±9.26126.39±12.073820135.48±23.0798.00±7.83101.79±5.30103.97±7.62122.17±11.48136.34±11.974318166.86±24.63101.08±6.94105.11±4.75108.18±6.70129.15±9.26147.81±10.355842184.67±26.37102.36±6.72107.40±6.46112.57±8.48134.08±9.26155.73±10.696684210.49±28.86104.98±5.13110.29±4.60115.89±7.39140.27±8.76164.10±12.247336221.23±34.70105.29±5.58111.18±4.67117.55±5.56141.68±8.13167.77±13.178587261.82±44.16112.11±4.68117.44±5.00122.31±6.01154.34±13.80181.00±14.629589266.45±38.93113.63±4.66117.86±4.88120.04±6.09156.81±10.74185.10±11.510128312.60±47.75116.79±4.97122.79±6.36124.28±6.58163.01±10.38193.44±12.3411349356.16±44.44118.24±4.68124.62±5.68129.79±8.15168.73±9.08198.63±11.3712775401.78±56.33121.36±4.63128.12±4.92133.39±6.99174.31±9.24204.48±12.3513692441.88±53.36123.39±4.29130.20±4.59136.19±8.14180.67±7.75212.82±9.4614545475.70±47.24124.97±4.40131.63±4.88141.69±7.45184.44±7.84216.24±8.8915657485.56±54.62126.51±4.09132.89±4.99144.42±8.67187.38±8.91219.09±9.9616664494.86±54.10127.07±4.77133.55±5.68144.79±8.02189.30±7.08219.60±17.5017857500.91±56.22128.27±4.39135.10±4.14145.28±7.11190.98±7.44219.65±8.6018384518.36±64.09128.97±4.30135.70±2.91146.86±9.22193.44±10.93221.23±9.0319223536.90±41.77131.25±4.07135.71±2.98147.92±5.60195.83±8.31223.42±8.1820189557.43±41.36132.20±2.17140.20±3.49147.97±6.79199.00±5.62228.67±3.78
表3Gompertz、Bertallanff、Logistic和Brody模型各指标的相关估计值
Table3EstimatedvaluesofGompertz,Bertallanff,LogisticandBrodymodelforbodymassindexes
模型Model参数Parameter体重/kgBodyweight体高/cmWithersheight体斜长/cmBodylength十字部高/cmHipheight胸围/cmChestcircumference腹围/cmAbdominalgirthGompertzA764.00131.20147.60139.80202.20227.40B2.720.17420.72139.800.921.04k0.120.16520.180.160.160.20R20.98760.99510.99580.99830.99690.9969LogisticA617.20130.50145.40138.00196.60222.00B8.760.56740.99580.731.391.68k0.230.17750.230.190.210.27R20.98740.99440.99550.99820.99670.9966BertallanffyA831.40129.00148.60140.60205.000.27B0.630.73350.220.170.270.30k0.080.21450.170.150.140.18R20.98760.99180.99590.99830.99700.9970BrodyA651.20132.70151.20142.50213.10238.30B0.530.44540.530.450.630.67k0.140.14070.140.130.110.13R20.98740.99660.99600.99830.99720.9972
表4Gompertz、Bertallanff和Logistic模型对体重指标的相关估计值
Table4EstimatedvaluesofGompertz,BertallanffandLogisticmodelsforbodyweightindexes

生长模型Growthmodel拐点月龄Inflectionpointmonth拐点体重/kgInflectionpointbodyweight最大日增重/kgMaximumdailygain相对生长率RelativegrowthrateGompertz8.47281.811.0510.1251Bertallanff7.15268.621.0070.1328Logistic9.46308.551.1400.1235
2.3 利用4种模型绘制西门塔尔肉牛体尺和体重的生长曲线
4种数学模型对肉用西门塔尔牛体重、体尺的拟合结果如图1所示,出生到20月龄的肉用西门塔尔牛生长阶段4种模型理论值呈逐渐稳步上升的趋势。犊牛从出生到12月龄上升较快之后则逐渐平缓,且4种模型对不同体尺性状的拟合效果较一致,导致图中出现了4种曲线重叠的现象。而Gompertz和Bertallanffy两种模型对体重的拟合优于其他两种模型,这说明,对于该地区的肉用西门塔尔牛来说,这两个模型更能反映出本群体的生长发育规律。而且,Gompertz模型得到的最大体重可达到831.40 kg,是4种模型中最佳值,因此,对乌拉盖地区肉用西门塔尔牛体重拟合的最佳模型是Gompertz。Brody模型对体高、体斜长、胸围、腹围和十字部高的拟合效果均最优,结果分别为132.7、151.20、213.10、238.30、217.65和142.50 cm,较其他模型高出0.3~7.1 cm。

图中GOMP_M、Logi_M、Bert_M、Brody_M 分别代表模型Gompertz、Logistic、Bertallanff和Brody, BW、BL、CC、WH、HH、AG分别代表体重、体斜长、胸围、体高、十字部高和腹围GOMP_M, Logi_M, Bert_M, Brody_M represent models Gompertz, Logistic, Bertallanff and Brody, respectively, the BW,BL,CC,WH,HH,AG represent body weight, body length, chest circumference, withers height, hip height, abdominal grith, respectively图1 利用4种模型绘制西门塔尔肉牛体尺和体重的生长曲线Fig.1 Using the 4 models to draw the growth curves of the body measurements and body weight of Simmental beef cattle
2.4 肉用西门塔尔牛体重与体尺的相关性分析
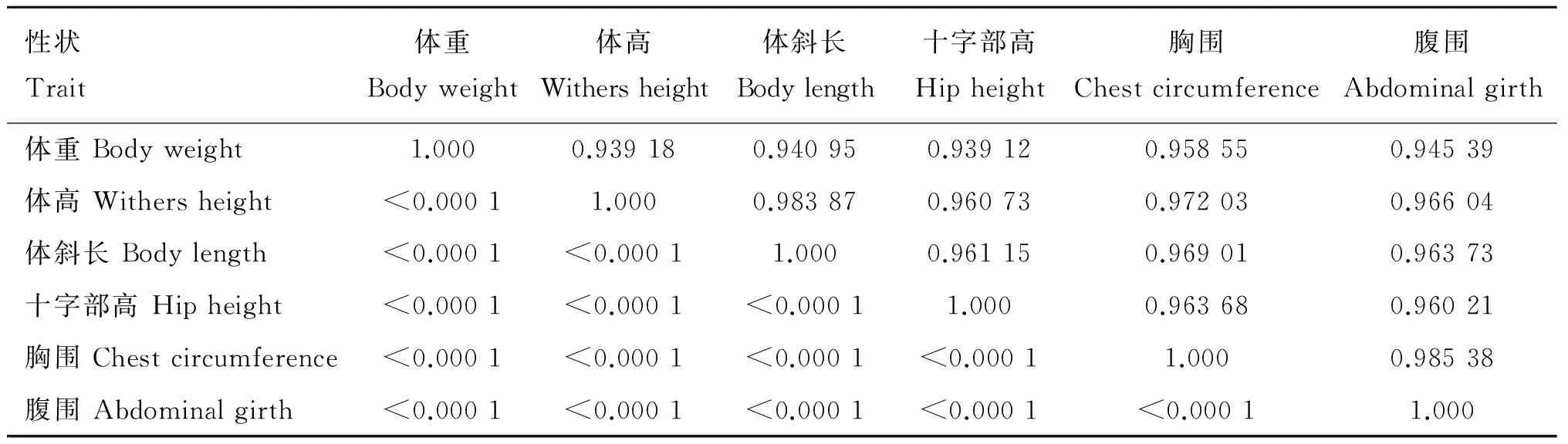
由表5可知,右上侧为各性状间的相关系数,左下侧是各性状相关关系显著性的检验结果。体重与体高、体斜长、十字部高、胸围和腹围的相关性较高,其中体重与胸围的相关性最高(r=0.958 55),腹围次之;体高与体斜长相关性最高(r=0.983 87),胸围次之。因此,肉用西门塔尔牛6个性状指标间呈极显著相关,其中胸围和腹围是可直接用来反映体重大小的最重要的两个指标。
2.5 肉用西门塔尔牛体尺与体重的线性回归分析
2.5.1肉用西门塔尔牛体尺与体重的线性回归分析通过SAS软件分析表明,剔除与体重回归关系不显著的体高和十字部高,体斜长、胸围和腹围与体重的回归关系极显著(P<0.000 1),检验结果见表6和表7。建立回归方程:Y=-366.485 70+1.307 37X3+3.896 12X4-0.417 50X5。
表5肉用西门塔尔牛各性状指标间的相关性
Table5ThecorrelationanalysisamongdifferenttraitsofSimmentalbeefcattle
性状Trait体重Bodyweight体高Withersheight体斜长Bodylength十字部高Hipheight胸围Chestcircumference腹围Abdominalgirth体重Bodyweight1.0000.939180.940950.939120.958550.94539体高Withersheight<0.00011.0000.983870.960730.972030.96604体斜长Bodylength<0.0001<0.00011.0000.961150.969010.96373十字部高Hipheight<0.0001<0.0001<0.00011.0000.963680.96021胸围Chestcircumference<0.0001<0.0001<0.0001<0.00011.0000.98538腹围Abdominalgirth<0.0001<0.0001<0.0001<0.0001<0.00011.000
表6肉用西门塔尔牛体斜长、胸围、腹围与体重回归关系的显著性检验
Table6Thesignificancetestoftheregressionrelationshipbetweenthebodylength,chestcircumference,abdominalgirthandbodyweightofSimmentalbeefcattle

源Source自由度Degreeoffreedom(df)平方和Sumofsquares均方MeansquareF值F-valuePr>F模型Model4462920911573021608.76<0.0001误差Error541389182719.37515校正合计Total5455018391
表7肉用西门塔尔牛体斜长、胸围、腹围与体重的回归系数
Table7Theregressioncoefficientsbetweenthebodylength,chestcircumference,abdominalgirthandbodyweightofSimmentalbeefcattle
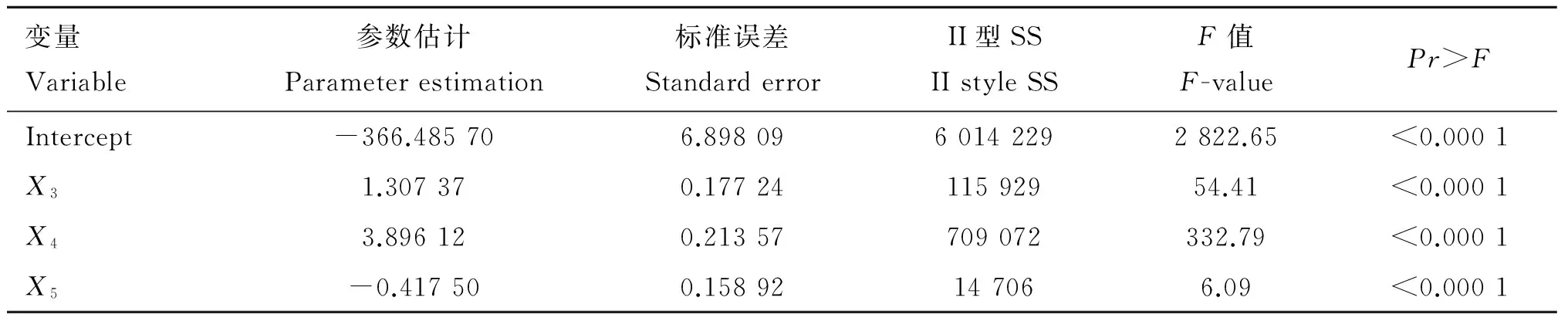
变量Variable参数估计Parameterestimation标准误差StandarderrorII型SSIIstyleSSF值F-valuePr>FIntercept-366.485706.8980960142292822.65<0.0001X31.307370.1772411592954.41<0.0001X43.896120.21357709072332.79<0.0001X5-0.417500.15892147066.09<0.0001
2.5.2肉用西门塔尔牛体重回归预测方程的验证为了能够进一步验证由以上分析所得出的肉用西门塔尔牛体重回归预测方程的实用性,选取该地区12月龄肉用西门塔尔牛共计125头个体数据代入所得回归预测方程计算出回归预测体重。通过SAS 9.4软件的配对样本t检验当μ=0 时用t分布函数95%区间内来判断肉用西门塔尔牛实测体重与回归预测体重之间的差异性,两组体重数据间的相关系数为0.927 4(P<0.001),检验结果如表8所示,实测体重与回归预测体重之间无显著性差异(P=0.095),证实了乌拉盖地区肉用西门塔尔牛体重回归预测方程Y=-366.48 570+1.307 37X3+3.896 12X4-0.417 50X5具有统计学意义。
表8肉用西门塔尔牛实测体重与回归方程预测体重样本配对t检验
Table8SamplepairingttestofthemeasuredbodyweightandpredictedbodyweightbyregressionequationofSimmentalbeefcattle

性状Trait平均值Mean标准差SD标准误SE上限Lower下限Uppert自由度Df双侧P值Pvaluesonbothsides实际体重Actualbodyweight401.2547.792.303.44-7.52-0.741250.095预测体重Predictedbodyweight402.2130.282.77
3 讨 论
3.1 肉用西门塔尔牛体重生长曲线模型的讨论
前人通过研究比较不同模型来分析母牛的生长发育[23],一致认为用Brody模型描述母牛生长发育过程效果较差,这些牛品种包括安西母牛、延边母牛、秦川母牛、徽成母牛、安格斯母牛、海福特母牛和娟姗母牛。而本研究选取乌拉盖地区肉用西门塔尔牛从出生到20月龄的体重和体尺测量数据进行分析发现,4种生长曲线模型对体重和体尺性状都能够得到很好的拟合。动物生长曲线模型实质上是把动物生长过程中各个阶段的体重和体尺的数据资料提供的信息综合成少数几个可表现具体生物学意义的参数[24]。动物生长曲线的分析和拟合也是研究畜禽生长发育规律的主要方法之一,尤其是国外许多知名牛品种已通过多种数学模型建立了适合该品种的生长曲线方程[13,18],为个体选育提供数据支持。熊飞等[25]通过对槟榔江水牛的体重和体尺性状进行累计生长曲线的预测方程拟合发现,槟榔江水牛在犊牛时期的生长发育较快,其新陈代谢能力相对旺盛,而成年后则逐步趋于稳定。本研究中所应用的4种非线性模型中,Brody模型仅仅是描述渐近生长过程;Logistic、Gompertz是拐点固定的S形生长曲线模型[26];Bertalantfy是拐点可变的S形生长曲线模型。Logistic模型拐点在极限体重的1/2处拐点体重为0.5A,该模型适用于早期生长慢、生长拐点较迟的牛品种。Gompertz模型拐点在极限体重的1/e处,拐点体重为0.368A,所以Gompertz模型适合描述早期生长迅速的生长过程,也是当前使用较多的生长曲线模型。对于本试验群体,由于早期生长迅速,Gompertz模型拟合结果达到0.987 6,是4种模型中最好的,能很好的反映该品种的生长特性从而指导选育。
本研究所选试验群体数据是来自内蒙古乌拉盖地区肉用西门塔尔牛不同年份各生长阶段的体重体尺记录,乌拉盖地区属森林草原向典型草原过渡地带,以典型草原为主,气候属半湿润、半干旱大陆性气候,气温低,冷季较长,年均气温为-0.9 ℃,水资源丰富。本地肉用西门塔尔牛一般以放养为主,自由采食,生长速度较快,体型大,是优良的牛品种。通过对体重体尺生长曲线模型的分析发现,犊牛的体尺和体重在出生至1周岁上升速度较快。乌拉盖地区肉用西门塔尔牛的成熟体重为617.2~831.4 kg,这与陈江凌等[27]对荷斯坦、西门塔尔、夏洛莱、利木赞和红安格斯牛用Bert模型得到的成熟体重793.7~1 081.2 kg存在差距,主要是因为所测牛只进行3月龄早期断奶及6月龄分群饲养,由于受饲养、管理、天气、饲喂条件等因素制约,致使生长过程出现较大偏差。根据张丽[18]和左福元[15]等分别对南阳母牛和金黄阿奎顿杂交后代牛与黑安格斯杂交牛体重生长拐点的研究发现,南阳母牛(4.41月龄,113.77 kg)、金黄阿奎顿杂交牛后代(4.16月龄,71.83 kg)和黑安格斯杂交牛(4.97月龄,78.38 kg)生长拐点都出现在4月龄,而德国对西门塔尔杂交后代牛体重生长拐点的研究发现,拐点月龄为9.58月龄时体重是115.23 kg,本研究的肉用西门塔尔牛群体利用Gompertz 模型得到拐点月龄为8.47,此时的拐点体重为281.81 kg, Logistic模型则分别为9.46月龄和308.55 kg,是前人所报道的拐点体重的2倍。品种早熟性决定牛体重拐点时间,拐点时间越晚则表示该品种成熟越晚,体型更大。
3.2 肉用西门塔尔牛体尺与体重相关性和回归性的分析
畜禽体型外貌是遗传因素与环境因素相互作用的结果。与其他牛品种相比,新疆褐牛的体型外貌、尻部、后躯对品种特征、生产性能方面的影响非常大[28-29]。而肉用西门塔尔牛后备牛以达到理想的生长指标且14~15月龄可以配种(体高127 cm、体重360 kg)为主要目标[30-31]。肉用西门塔尔牛的体重和体尺是反映该群体身体结构及发育程度的重要指标,是用来衡量其经济用途最直接的依据之一。体尺测量是采用专门的工具对家畜各部位进行准确度量,研究本品种外貌特征、估计体重及生产性能的重要手段之一,不同月龄肉用西门塔尔牛体尺生长发育速度不同。通过对肉用西门塔尔牛进行相关性分析可知,体尺性状与体重之间均呈极显著正相关,各个体尺性状通过直接或间接的作用对体重产生影响。体尺与体重的相关性系数大小依次为胸围>腹围>体斜长>体高>十字部高。由此可以发现,胸围和腹围与体重的相关性系数分别达到0.958 55和0.945 39,是对体重产生影响最大的指标。在生产实践中应加以重视与体重相关性高的指标,提高经济效益。
多元线性分析是统计分析及建立预测方程的重要手段。通过对乌拉盖地区肉用西门塔尔牛体高、十字部高、体斜长、胸围、腹围与体重的线性回归分析,利用向前回归剔除显著性不明显的X1、X2和X3后得到体斜长、胸围、腹围与体重新的预测方程:Y=-366.485 70+1.307 37X3+3.896 12X4-0.417 50X5,并一步验证了该方程的实用性,预测体重与实际体重间无显著差异,该拟合方程有较好的估测能力。通过该研究可以看出,不同年龄的肉用西门塔尔牛在所研究阶段体重与体尺性状均呈一定程度的波动状态。
4 结 论
本研究通过对内蒙古乌拉盖地区肉用西门塔尔牛群体的体重、体高、体斜长、十字部高、胸围和腹围等指标数据的生长发育规律进行研究和分析发现,Gompertz和Bertallanffy两种模型对体重的拟合优于其他两种模型,Brody模型对体高、体斜长、胸围、腹围和十字部高的拟合效果均最优。通过SAS 9.4软件的配对样本t检验,当μ=0的t分布函数用95%区间内来判断肉用西门塔尔牛实测体重与回归预测体重之间的差异性,两组体重数据之间的相关系数为0.927(P<0.001),实测体重与回归预测体重之间无显著性差异(P<0.001),预测体重回归方程:Y=-366.485 70+1.307 37X3+3.896 12X4-0.417 50X5,可应用于估测肉用西门塔尔牛体重的生产实践中,为乌拉盖地区肉用西门塔尔牛的选育提供相应的数据支持。
参考文献(References):
[1]王雅春, 陈幼春. 世界西门塔尔牛育种现状及其在中国的应用方向[J].中国牛业科学, 2008, 34(6): 1-4.
WANG Y C, CHEN Y C. Breeding progress of simmental World-wide and the Principle of its application in China[J].ChinaIndustryScience, 2008, 34(6): 1-4. (in Chinese)
[2]许尚忠, 李俊雅, 任红艳, 等. 中国西门塔尔牛选育及其进展[J].中国畜禽种业, 2008, 4(5): 13-15.
XU S Z, LI J Y, REN H Y, et al. Chinese simmental breeding and its progress[J].TheChineseLivestockandPoultryBreeding, 2008, 4(5): 13-15. (in Chinese)
[3]方晓敏, 许尚忠, 张英汉, 等. 我国新的牛种资源——中国西门塔尔牛[J].黄牛杂志, 2002, 28(5): 67-69.
FANG X M, XU S Z, ZHANG Y H, et al. The new kind of resources-Chinese simmental cattle[J].JournalofYellowCattleScience, 2002, 28(5): 67-69. (in Chinese)
[4]FAN H Z, WU Y, ZHOU X J, et al. Pathway-based genome-wide association studies for two meat production traits in simmental cattle[J].SciRep, 2015, 5: 18389.
[5]WU Y, FAN H Z, WANG Y H, et al. Genome-wide association studies using haplotypes and individual SNPs in Simmental cattle[J].PLoSOne, 2014, 9(10): e109330.
[6]NIU H, ZHU B, GUO P, et al. Estimation of linkage disequilibrium levels and haplotype block structure in Chinese Simmental and Wagyu beef cattle using high-density genotypes[J].LivestSci, 2016, 190: 1-9.
[7]XIA J W, QI X, WU Y, et al. Genome-wide association study identifies loci and candidate genes for meat quality traits in Simmental beef cattle[J].MammGenome, 2016, 27(5-6): 246-255.
[8]ZHU B, NIU H, ZHANG W G, et al. Genome wide association study and genomic prediction for fatty acid composition in Chinese Simmental beef cattle using high density SNP array[J].BMCGenomics,2017, 18: 464.
[9]ZHU B, ZHU M, JIANG J C, et al. The impact of variable degrees of freedom and scale parameters in bayesian methods for genomic prediction in Chinese simmental beef cattle[J].PLoSOne, 2016, 11(5): e0154118.
[10]牛红, 宝金山, 吴洋, 等. 中国西门塔尔牛肉用群体重要经济性状遗传参数估计[J].畜牧兽医学报, 2016, 47(9): 1817-1823.
NIU H, BAO J S, WU Y, et al. Estimation of genetic parameters for economic important traits in Chinese Simmental beef cattle[J].ActaVeterinariaetZootechnicaSinica, 2016, 47(9): 1817-1823. (in Chinese)
[11]杨运清, 缪尧源. 动物生长曲线拟合方法的探讨[J].畜牧兽医学报, 1992, 23(3): 219-224.
YANG Y Q, MIAO Y Y. Animal growth curve fitting method discussion[J].ActaVeterinariaetZootechnicaSinica,1992, 23(3): 219-224. (in Chinese)
[12]杨运清. 动物生长模型的优化拟合方法[J].数理统计与管理, 1991, 10(5): 43-48.
YANG Y Q. Animal growth model of the optimum fitting method[J].ApplicationofStatisticsandManagement,1991, 10(5): 43-48. (in Chinese)
[14]BULLOCK K D, BERTRAND J K, BENYSHEK L L. Genetic and environmental parameters for mature weight and other growth measures in Polled Hereford cattle[J].JAnimSci, 1993, 71(7): 1737-1741.
[15]左福元, 王玲, 周沛, 等. 三峡库区川南山地黄牛及杂种后代生长曲线拟合分析[J].中国畜牧杂志, 2010, 46(9): 1-4.
ZUO F Y, WANG L, ZHOU P, et al. Analysis of growth curve of Chuannan Mountainous cattles and their hybrids in Three Gorges Reservoir Area[J].ChineseJournalofAnimalScience,2010, 46(9): 1-4. (in Chinese)
[16]杨晓冰, 陈宏, 滑留帅, 等. 固原地区秦川牛利杂群体生长曲线拟合分析[J].中国牛业科学, 2011, 37(6): 4-7.
YANG X B, CHEN H, HUA L S, et al. Growth curve analysis of Limousin×Qinchuan cattle in Guyuan Region[J].ChinaCattleScience,2011, 37(6): 4-7. (in Chinese)
[17]杨敏, 朱化彬, 殷宗俊, 等. 皮南肉牛选育初期的生长曲线分析[C]//第三届中国牛业发展大会论文集. 穆棱: 中国畜牧业协会, 2008.
YANG M, ZHU H B, YIN Z J, et al. Skin south beef cattle breeding in the early growth curve analysis[C]//The Third China Industry Development Conference. Muling: China Animal Agriculture Association, 2008. (in Chinese)
[18]张丽, 张良志, 张爱玲. 南阳黄牛体重曲线拟合的比较分析[J].广东海洋大学学报, 2008, 28(1): 98-100.
ZANG L, ZHANG L Z, ZHANG A L, et al. The comparison of Nanyang cattle weight curve fitting analysi[J].JournalofGuangdongOceanUniversity, 2008, 28(1): 98-100. (in Chinese)
[19]马光辉, 张文龙, 黄锡霞, 等. 新疆地区西门塔尔牛不同模型泌乳曲线拟合效果分析[J].新疆农业科学, 2013, 50(10): 1931-1936, 1930.
MA G H, ZHANG W L, HUANG X X, et al. Analysis of fitting effect on different models of lactation curve for Simmental Cattle in Xinjiang[J].XinjiangAgriculturalSciences, 2013, 50(10): 1931-1936, 1930. (in Chinese)
[20]杨运清, 杨玉林. 动物生长模型参数的常规估计法[J].东北农业大学学报, 1994, 25(2): 132-137.
YANG Y Q, YANG Y L. Routine parameter estimation methods for animal growth models[J].JournalofNortheastAgriculturalUniversity, 1994, 25(2): 132-137. (in Chinese)
[21]胡良平. 《Windows SAS6.12 & 8.0实用统计分析教程》出版[J].中华医学杂志, 2001, 81(8): 475.
HU L P. 《Windows SAS6.12 & 8.0 Practical statistical analysis tutorial》published[J].NationalMedicalJournalofChina, 2001, 81(8): 475. (in Chinese)
[22]于志, 高艳霞, 曹玉凤, 等. 中国荷斯坦犊牛和育成牛生长发育规律的研究[J].中国畜牧兽医, 2014, 41(6): 121-125.
YU Z, GAO Y X, CAO Y F, et al. Study on growth and development pattern of Chinese Holstein Calf and Heifer[J].ChinaAnimalHusbandry&VeterinaryMedicine, 2014, 41(6): 121-125. (in Chinese)
[23]张文举. 徽成盆地黄牛生长曲线方程的研究[J].甘肃畜牧兽医, 1998, 28(1): 3-6.
ZHANG W J. Cattle growth curve equation of the badge into basin research[J].GansuAnimalandVeterinarySciences,1998, 28(1): 3-6. (in Chinese)
[24]LARID A K. Postnatal growth of birds and mammals[J].Growth, 1966, 30(3): 349-363.
[25]熊飞, 苗永旺, 李大林, 等. 槟榔江水牛体重及体尺生长规律的研究[J].云南农业大学学报, 2011, 26(4):472-478.
XIONG F, MIAO Y W, LI D L, et al. Growth regularities of body weight and size of Binglangjiang buf-falo[J].JournalofYunnanAgriculturalUniversity,2011, 26(4): 472-478. (in Chinese)
[26]DARMANI KUHI H, KEBREAB E, LOPEZ S, et al. An evaluation of different growth functions for describing the profile of live weight with time (age) in meat and egg strains of chicken[J].PoultSci, 2003, 82(10): 1536-1543.
[27]陈江凌, 汪聪勇, 耿繁军. 种公牛早期生长曲线分析[J].安徽农业科学, 2014, 42(14): 4352-4353.
CHEN J L, WANG C Y, GENG F J. Analysis of growth curve of growing bulls[J].JournalofAnhuiAgriculturalSciences, 2014, 42(14): 4352-4353. (in Chinese)
[28]姚亚铃. 湘西黄牛生长发育规律及杂交利用效果研究[D]. 长沙: 湖南农业大学, 2006.
YAO Y L. Study on Xiangxi Cattle growth developmental mechanism and utilization of hybrid effect[D]. Changsha: Hunan Agricultural University, 2006. (in Chinese)
[29]马茂华, 孔令韶. 新疆呼图壁种牛场地区13种优势植物水溶性盐分的含量特点及数量分析[J].生态学报, 1996, 16(5): 509-516.
MA M H, KONG L S. Quantitative analysis and characteristics of water-soluble salt contents in 13 dominant plant species in the area of Hutubi cattle farm, Xinjiang[J].ActaEcologicaSinica, 1996, 16(5): 509-516. (in Chinese)
[30]张世元, 张伟. 西门塔尔后备牛的培育[J].新疆畜牧业, 2011(4): 32-35.
ZHANG S Y, ZHANG W. Simon tal replacement cattle breeding[J].JournalofAnimalHusbandryinXinjiang, 2011(4): 32-35. (in Chinese)
[31]付雪峰, 季生林, 黄锡霞, 等. 舍饲新疆褐牛犊牛体重与体尺指标的相关及回归分析[J].新疆农业科学, 2009, 46(4): 844-848.
FU X F, JI S L, HUANG X X, et al. Correlation and regression analysis of body weight and body size measurements for Xinjiang Brown cattle calf under pen feeding[J].XinjiangAgriculturalSciences, 2009, 46(4): 844-848. (in Chinese)
