纵横几何,探索规律—例谈初中几何的题组教学

广东省广州市华师附中番禺学校(511442)　古敏锋

初中数学几何部分对于中学数学教学来说非常重要,得几何者得中考数学天下,这句话一点也不夸张.然而对于大多数初中学生来说,几何部分却是条拦路虎,在面对一道题目时,由于所学过的几何定理、推论太多,学生往往觉得无从下手;有时感觉题目似曾相识,却又有所不同,陷入思维困惑中.因此,对于初中数学教师来说,如何提升学生几何问题解决能力是个值得探究的问题.

事实上,在教学中我们可以发现,几何题目虽千千万万,但总会发现有些题目图形特征相似或同类,有其基础模型,例如“蝴蝶型”、“A字型”、“平行线+角平分线”等.如果教师能够在教学中对几何题目进行分类,渗透基本模型,通过简单例题浅析初中几何的基础模型,通过简单例题的变式进行题组教学,引导学生探索几何规律及问题解决方法,那么在万千题海中学生也能较好地分析问题、解决问题.以下将展示三个题组教学的案例.

案例一三角形的角平分线的题组教学

例 1如图 1,△ABC中,∠A=40°,当∠ACB、∠ABC的平分线交于点O时,则∠BOC=____.

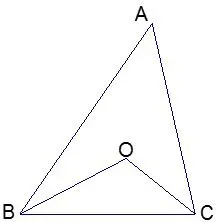
图1

引导解决该问题,我们可以使用三角形的内角和定理,或三角形的外角和定理.∠ABC+∠ACB=180°−∠A;∠BOC=180°−(∠OBC+∠OCB).

变式1如图1,在△ABC中,∠ACB、∠ABC的平分线交于点O.

(1)若∠A=α,则 ∠BOC=____.

(2)若 ∠BOC=140°,则 ∠A=___;若 ∠BOC=β,则∠A=____.

变式1是由特殊到一般,是对角平分线性质定理的直接应用,让学生从具体到抽象,初步应用几何的简单符号书写.

变式2如图,△ABC中,已知∠A=40°.(1)如图1,当∠ACB、∠ABC的平分线交于点O时,则∠BOC=___;(2)如图2,当∠ABC的平分线BD与∠ACB的外角平分线交于点O时,则∠BOC=___;(3)如图 3,当 ∠ABC的外角平分线与∠ACB的外角平分线交于点O时,则∠BOC=___.

图1

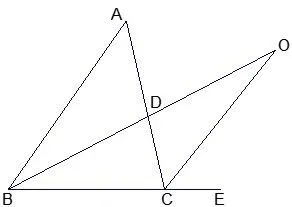
图2

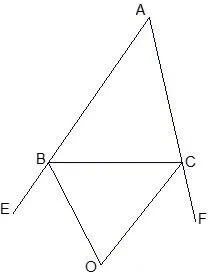
图3

变式2帮助学生加深对三角形内、外角的理解,及对角平分线位置的理解.

案例二证明三角形全等(以“边角边”为例)的题组教学

例2如图1,AD、BE相交于点C,CA=CD,CE=CB.求证:AB=DE.

变式1如图2,CA=CD,CE=CB,∠1=∠2.求证:AB=DE.

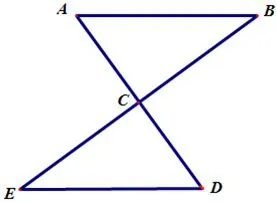
图1

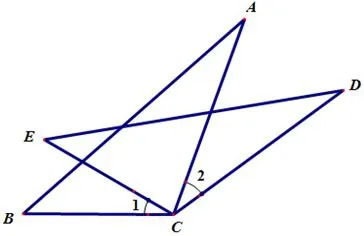
图2

变式2如图3,OC是∠AOB的平分线,P是OC上一点,PD⊥OA交OA于D,PE⊥OB交OB于E.F是OC上另一点,连接DF,EF求证:△PDF～=△PEF.

变式3如图4,AB=DE,AC=DF,BE=CF.求证:AB//DE,AC//DF.

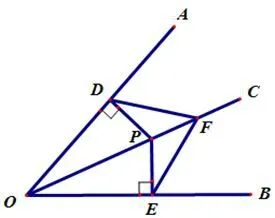
图3

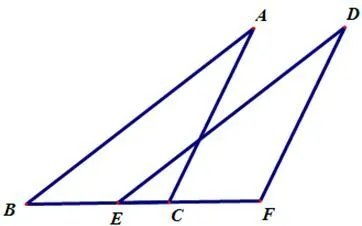
图4

本组题组教学由浅入深,是对三角形全等的性质及判定的学习应用,知识、难度逐层递增能更好地让学生理解几何图形的“性质、判定”的不同之处.题组中展示了四个层次教学:

层次一:直接(或间接)给出全部条件证明全等,然后直接得出结论.

层次二:先证明一个条件成立,再证明全等,然后直接得出结论.

层次三:先证明两个条件成立,再证明全等,然后直接得出结论.

层次四:证明全等后,得出中间结论,再证明最终结论.

在分析引导过程中,渗透几何证明的分析法与综合法.

案例三证明线段的和差的题组教学

在求线段的和差问题中,我们解决问题的思路是“截长补短”.而在这一类问题中,我们常见的模型是“一线三等角”.

例1在△ABC中,∠BAC=90°,AB=AC,直线m经过点A.已知BD垂直直线m,CE垂直直线m,垂足分别为点D,E,证明:DE=BD+CE.

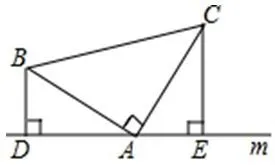
图1

我们可以将本题由特殊到一般,更改特殊角.

变式1:如图将1中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?如果成立,请你给出证明,若不成立,请说明理由.

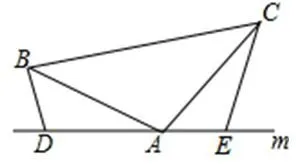
图2

甚至,我们可以将“两角”的位置改变.

变式2在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.

(1)当直线MN绕点C旋转到图3-1的位置时,试说明△ADC～=△CEB;

(2)当直线MN绕点C旋转到图3-2的位置时,试说明DE、AD、BE具有什么数量关系?并说明理由.

(3)当直线MN绕点C旋转到图3-3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并说明理由.

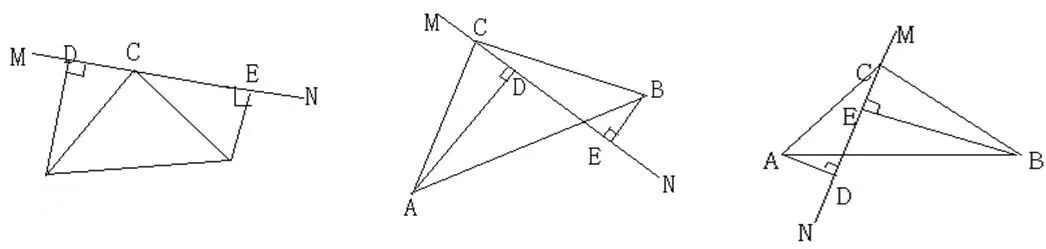
图3

由以上三个案例可以看到,在根据学生的认知规律情况下,对一个几何问题可设计一个由浅入深、由表及里的阶梯性的问题系列,采用变式题组教学,从而使问题具有层次性,满足各层次学生需求.

当然,进行题组教学时,教师需要注意以下几点:首先,题组教学时的选题、编题应有利于巩固基础知识、基本方法和揭示某些解题规律,每个题组中应做到由易到难,由单一到综合,同时要紧紧围绕课堂教学目标;其次,题组教学需安排反思总结环节,对于一组变式教师可引导学生回过来反思,本题组复习了哪里基础知识?利用了哪些基本技能?哪道题可以推广,即再引申变式?把疑问交给学生,使他们不断地反思,在反思中巩固、深化、提高,理解和巩固概念、法则、公式、定理,使他们的知识由点到面、由面到体、形成合理的知识结构,同时提高发现、分析和解决问题的能力;最后,题组教学时应能及时根据学生的反馈随时调节教学,奥苏贝尔教授说过:“影响学生学习的最重要的因素是学生已经知道了什么.”教师要及时了解学生掌握了什么?还未掌握什么?哪些学生掌握了?哪些学生还未掌握?······进而根据学生的情况调整教学安排,从而提高教学效率,确实提高学生解决几何问题的能力.