小知识,大联系

山东省菏泽一中(274000)　段宇飞

平面向量是数学中的重要内容,也是高中数学中的工具性知识,它具有代数和几何的双重身份,融数、形于一体,是沟通代数与几何的桥梁.能高中数学中多个知识交汇.向量也是沟通物理知识的桥梁,物理中的力、位移、速度、加速度等都可以用向量来表示.同时,向量也在日常生活中有重要的运用.

一、平面向量与其它数学知识的联系

1.平面向量的代数运算与函数的联系

由于平面向量的坐标与函数图象相对应,使函数图象及图象与平面向理产生密切的联系,形成数学知识交汇的一个网点.

例 1若是非零向量,且则函数是 ()

A.一次函数且是奇函数

B.一次函数但不是奇函数

C.二次函数且是偶函数

D.二次函数但不是偶函数

分析本题利用平面向量的数量积是一个实数,将平面向量与函数结合起来.由于平面向量的运算可经是坐标运算,所以通常通过以下知识,将平面向量与函数联系起来.

2.平面向量的代数运算与方程的联系

平面向量的代数运算是坐标运算,常常与方程联系要一起,也是形成数学知识网络的一个交汇点.

例 2已知点A(−1,−1)、B(1,3)、C(x,5),若对于平面上任意一点O,都有则x=___.

分析利用平面向量的代数运算,通过建立方程(组),来解决实际问题.建立方程(组),除胃上述知识外,还通常通过以下知识将平面向量与方程(组)联系起来.

(3)设点A(x1,y1),B(x2,y2),则

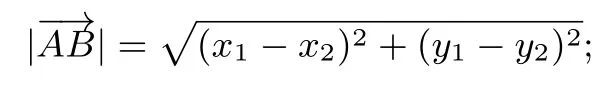
3.平面向量的代数运算与不等式的联系

平面向量的代数运算是坐标运算,常常与不等式联系要一起,也是形成数学知识网络的一个交汇点.

例3下列命题中,正确的是()

分析利用平面向量的代数运算,建立平面向量与不等式之间的联系.

4.平面向量与三角函数之间的联系

平面向量的夹角是平面向量与三角函数联系在一起的主要原因.从而形成了数学知识网络的一个交汇点.

例4在△ABC中,角A,B,C的对边分别为a,b,c.已知向量=(a+c,b−a),=(a−c,b),且

(I)求角C的大小;

(II)若sinA+sinB=求角A的值.

分析利用平面向量中两向量的夹角,沟通了平面向量与三角形的联系.

5.平面向量与几何的联系

向量的数量积与距离、角度紧密相联,它是度量几何学的基础.如何度量距离和角度是几何学发展两个强大的动力.从直接度量到相似和勾股计算,从解直角三角形,到正弦和余弦定理,人们已可解决各种各样的有关角度和距离的度量.向量的数量积使度量几何上升到一个崭新的层面,使人们能更有效地用代数方法研究几何,向量的数量积已成为研究几何度量的强有力的工具.

(1)平面向量与平面解析几何的联系

平面向量具有数与形的双重特征,形是平面向量与几何联系在一起的主要原因.

例 6已知直线l∶Ax+By+C=0,向量向量=(A,B),有下列说法:其中正确的有()

A.2个B.3个C.4个D.6个

分析利用平面向量是有向线段把平面向量与方向量、法向量联系在一起,沟通了平面向量与平面解析几何.

(2)平面向量与平面几何的联系

利用平面向量的几何表示与几何运算,是平面向量与平面几何产生联系的根本原因.

例7已知O,A,B是平面上的三个点,直线AB上有一点C,满足则=()

分析利用平面向量的几何运算,将平面向量与平面几何联系到一起,沟通了平面向量与平面几何.

6.平面向量与物理的联系

向量概念和运算,都有明确的物理背景.当向量与平面坐标系结合以后,向量的运算就可以完全转化为“代数”的计算,这就为我们解决物理问题带来极大的方便.

例8如图1,两条绳子提一个重物,每条绳子用力5N,这时两条强子的夹角为60°,则物体的重量G等于()

图1

分析利用平面向量的几何运算,将平面向量与物理问题联系到一起,沟通了平面向量与平面物理.

通过研究平面向量与不同数学知识与物理的联系,我理解了知识其实是相互联系的,所以学习知识应该“整体地学,联系地学”,才能真正理清知识结构,建立知识体系.

7.平面向量在生活的运用

平面向量可以用来解决现实生活中的许多问题,从而使平面向量用到了生活中的方方面面.

例1以某市人民广场的中心为原点建立直角坐标系,x轴指向东,y轴指向北一个单位表示实际路程100米,一人步行从广场入口处A(2,0)出发,始终沿一个方向均速前进,6分钟时路过少年宫C,10分钟后到达科技馆B(−3,5).求:(1)此人的位移向量;(2)此人行走的速度向量;(3)少年宫C点相对于广场中心所处的位置.

分析(1)AB的坐标等于它终点的坐标减去起点的坐标,代入A,B坐标可求;(2)习惯上单位取百米/小时,故需先将时间换成小时.而速度等于位移除以时间,由三角知识可求出坐标表示的速度向量.(3)通过向量的坐标运算及三角函数公式求解.

例2帆船是借助风帆推动船只在规定距离内竞速的一项水上运动.1900年第2届奥运会开始列为正式比赛项目,帆船的最大动力来源是”伯努利效应”.如果一帆船所受”伯努利效应”产生力的效果可使船向北偏东30°以速度20km/h行驶,而此时水的流向是正东,流速为20km/h.若不考虑其它因素,求帆船的速度与方向.

分析帆船水中行驶,受到两个速度影响:伯努利效应”产生力的效果为使船向北偏东30°,速度是20km/h,及水的流向是正东,流速为20km/h.这两个速度的和就为帆船行驶的速度.根据题意,建立数学模型,运用向量的坐标运算来解决问题.

例3某同学购买了x支A型笔,y支B型笔,A型笔的价格为m元,B型笔的价格为n元.把购买a、b型笔的数量x、y构成数量向量=(x,y),把价格m、n构成价格向量=(m,n). 则向量与的数量积表示的意义是____.

分析此题根据购卖A、B两种型号的笔的数量与价格构成了一个二元向量a,b.根据向量的数量积的运算公式可得=xm+ny.而xm表示购买A型笔所用的钱数;ny表示购买B型笔所用的钱数.所以向量的数量积表示的意义是购买两种笔所用的总钱数.