三角函数诱导公式的新记法

上海市华东师范大学教师教育学院(200062)　黄健

三角函数诱导公式,是高中生学习三角函数的基础,其目的是将任意角的三角函数转化为锐角的三角函数,便于计算.为后续的三角函数求值化简、简单证明以及三角函数图像和性质的学习等打好基础.由此可看出三角函数诱导公式的重要性.然而,三角函数的诱导公式繁多而且复杂,学生在初学三角函数的时候,很容易把一些公式混淆,并且总感觉记不牢.由于公式多,即使现在记住了,过后也可能很快忘掉,很多高中生都感到十分头痛.那有没有可以让学生很容易记住这些公式的方法呢?在此简单归纳诱导公式的记忆方法,同时提出在后期回顾复习和记忆时,可利用后续学习的三角函数图像帮助记忆诱导公式的新方法.

一、诱导公式记忆方法

1.口诀记忆法

“变”与“不变”是相对处于互余关系的函数而言的,sinα与cosα互余、tanα与cotα互余.

“向前看”就是根据“一正二正弦三切四余弦”(第一象限所有三角函数都是正的;第二象限正弦是正的;第三象限正切、余切是正的).

2.单位圆记忆法 [2]

新课标下三角函数的概念是放在直角坐标系下的单位圆中来定义的,为此,三角函数的所有的诱导公式都可以借助单位圆利用“角的终边的对称关系”的思想来理解和记忆.

又如,(2k+1)π+α(k∈)与α的终边关系,即π+α与α为的关系,而从α→π+α相当于把角的终边以坐标原点为旋转中心旋转π,于是(2k+1)π+α(k∈)与α的终边关于原点对称,设α的终边上一点P(x,y),则在(2k+1)π+α(k∈Z)的终边上的对应点P′(−x,−y).根据三角函数的定义,我们可以得到:sin((2k+1)π+α)=−sinα,cos((2k+1)π+α)=cosα.

类似其他几组诱导公式也可以用“角的终边的对称关系”来记忆,充分体现数形结合的思想.

二、利用函数图像记忆诱导公式的新方法

除了上面两类方法,我们还有其他的小方法可以帮助我们记忆,如利用周期性和奇偶性进行记忆等.不过相对来说较为局限,无法应用于所有诱导公式.

下面介绍的新方法是在学生已经学习了三角函数的图像的基础上进行的,所以可以在单元末复习、期末复习或高考前加强记忆时进行教学.

1.函数平移法

函数平移法可以在学生学习了三角函数的图像变换之后进行理解记忆.如记忆sin时,只需看成sinα的图像向左平移个单位长度,观察所得图像是 sinα、−sinα、cosα还是−cosα即可.如图所示,可得sin=cosα.

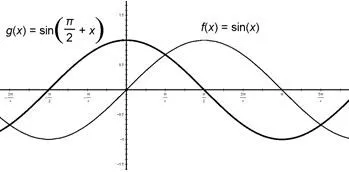
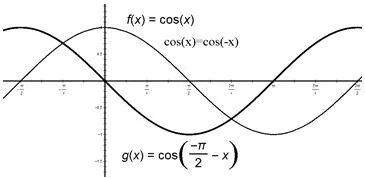
若α前为复号,则需认识到对称的含义.如cos的诱导公式,可看成是在cosα的基础上,先关于y轴对称,再向左平移个单位长度,得到−sinα.

2.函数绘制法

函数绘制法的原理同样是三角函数的图像变换,或者说是函数图像的本质.以前面两个诱导公式为例,先考虑sin我们可以将其看成在sinα图像的基础上,以为起点,向x轴的正向描绘函数图像,如图:

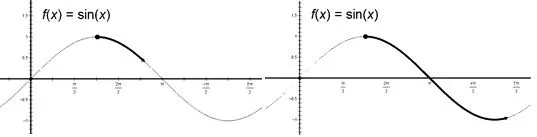
由此描绘出来的,即是以函数值1为起点,先递减至−1再递增的图像,明显为cosα的图像(如下图),故sin=cosα.

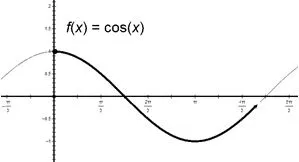
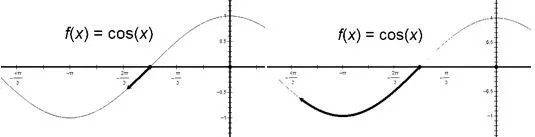
由此描绘出来的,即是以函数值0为起点,先递减至−1再递增的图像,明显为−sinα的图像(如下图),故cos=−sinα.

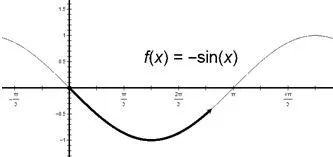
只要熟练掌握以上图像记忆方法,便可轻松得到任意诱导公式的结果,更可以加深对函数图像和三角函数函数平移的本质理解.以上方法为笔者高中时理解所得,一直沿用至今.且在多次家教和小班教学期间尝试用此方法帮助高二、高三学生(大部分学生忘记了诱导公式或者记混了诱导公式)记忆和理解三角诱导公式,并不定期进行记忆情况和运用情况的调查皆取得良好的效果.学生普遍认为,此方法能够很好地记忆诱导公式,比起一开始记忆时用的“口诀记忆法”(奇变偶不变,符号看象限)进行机械记忆来说,图像法的记忆更加牢固也更加准确.因此,新方法对记忆诱导公式、理解图像变换或者函数图像中自变量与因变量的关系等都有着巨大的作用.

三角函数诱导公式在高中数学三角函数一章中的重要性是不容忽视的.方法只是为掌握知识本身服务的,不管利用哪种方法来记忆诱导公式,我们的最终目标是能巧妙并准确地记忆公式本身,并能熟练地使用它来解决问题.

[1]廖佛成.三角函数诱导公式的三类记忆法[J].考试周刊,2014,31:61.

[2]杜彦军.三角函数诱导公式记忆新说[J].新课程学习(中),2012,04:136.