《一元二次方程试卷讲评课》的自我点评
2018-04-04广东省广州市海珠区聚德中学510305林彩满
广东省广州市海珠区聚德中学(510305) 林彩满
1 背景介绍
本课例是2016年9月20日上的试卷讲评课.这节课没经过试讲,是一节没经雕琢的平常课.与平时稍微不同的是,当时为了参加优课比赛,在9月18日整个年级统一测试后,我没有进行讲评,只是整理了一份答案给学生自行改正.9月19日测试了第二份试卷,第二份试卷的题目是第一份试卷题目的变式.这次录课的另一个不同:这是北京创先泰克科技有限公司帮忙拍摄,他们专业的拍摄也为这次优课能评上部优做了很大的贡献.
1.1 内容与学情分析
评讲内容是两次测试中,错误率比较高的题目.以题组的形式出现.任教班级学生的平均分在区统测时大约可以排在区第5名左右.
1.2 目标与目标解析
教法方面:通过题组练习,让学生更加意识到审题的重要性,感受题目形式不同,问法不同,所采用的方法也得相应改变.促使学生学会具体问题具体分析,不生搬硬套.通过成绩对比,让学生感受到自主学习的重要性,培养学生自主学习的习惯.从方法上的对比,让学生感受方法选择的重要性,引导学生在课后多与同伴交流.通过正误两类解法的展示,让学生学会如何有效检查.
学法指导方面:培养学生认真读题的习惯,逐步学会改编题目、自我修正的方法.
1.3 教学思路与理念
教学主线:题面的异同点,解法的变与知识点的不变.
理念:学习效果改变与学生本人态度改变有关,只有主动学习,类比地学,效率才会更高.
2 教学环节与环节评析
2.1 点评两次测试结果对比
(人数,前面数据是第1次人数,后面是第2次人数)
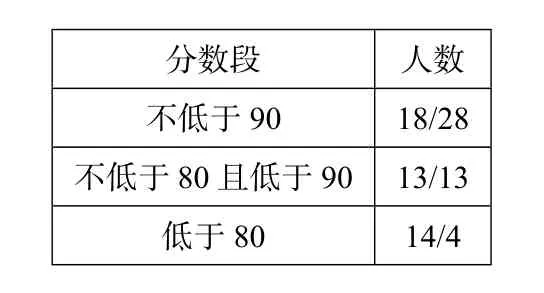
_________________________分数段 人数_____________________不低于9018/28__不低于80且低于90___13/13________________________低于8014/4_
2.2 点评
9个小组学生的分数变化,表扬进步大的学生、有合作精神的小组、学习态度优秀的同学.(该班45人,从初一开始就分为9个学习小组,5个女生小组,4个男生小组.刚开始的分组是同质分组,后期的小调整主要针对男同学,基本都有好、中、一般三个层次)
2.3 第1组题目讲评(方程有解)
若关于x的一元二次方程(x+2)2=k+1有解,则k的取值范围是___.
若关于x的一元二次方程x2+4x+3+k=0有解,则k的取值范围是____.
题目分析这是两道问法相同,形式不同的题目.主要想让学生引起注意的是,方法选择会因为形式的改变而改变.
学生板书:
何泳:k+1≥0,k≥−1.
黄浩文:x2+4x+4−k−1=0,x2+4x+3−k=0a=1,b=4,c=3−k b2−4ac≥0,16−4(−k+3)≥0,16+4k−12≥0 4k≥−4,k≥−1
谢雅岚:
a=1,b=4,c=3+k,∆=b2−4ac=16−4×1×(3+k)=16−12−4k=4−4k,因为有解,所以∆ ≥0,4−4k0,−4k≥−4,k≤1
学生郭逸希点评:把括号内的看成一个整体,根据一个数的平方的非负性(点评何泳的解法)
陈骏霖:以前做过类似的,习惯了这种方法(点评黄浩文的解法)
让学生点评的目的:引导学生从过程的繁简对比中,找到不同解法的共同点,更好地内化知识,更科学地选择方法.
2.4 第2组题目
若方程x2−6x+8=0的两根是某直角三角形的两直角边的长,则斜边长____.
若方程x2−kx+8=0的两根是某直角三角形的两直角边的长,则直角三角形的面积为___.
学生殷锦仁的板书:x2−6x+8=0,a=1,b=−6,c=8,x1+x2==(x1+x2)2−2x1x2=62−16=36−16=20.
卢颖欣:x2−kx+8=0,a=1,b=−k,c=8,x1x2==8,S=×8=4
李姝懿:x2−6x+8=0,x2−6x+9=1,(x−3)2=1,x−3=±1,x=3±1,x1=4,x2=
郭逸希的解法:x2−6x+8=0,(x−2)(x−4)=0,x1=2,x2=4
教师分别提问梁凯翔、莫志杰,为什么用到两根的积?为什么要求两根的平方和?让学生进一步意识到选择的方法跟题目所求有很大的关系.分析两种解法的优劣:能直接求的,用直接求的过程较简单;含参数的题型,用韦达定理更具普遍性,但得熟练掌握完全平方公式.
2.5 与上述题目解法相似的一道题目的简单讲评
已知关于x的一元二次方程
(1)求证方程x2−(2k+1)x+k(k+1)=0必有两个不等实数根(2)k为何值时,方程有一个正根和一个负根(求根公式)(3)若a,b为方程两个实数根,求k取何值时,a2+b2有最小值,最小值是多少?
本题在测试时,第(2)(3)小题完成情况不理想.学生不知道如何理解正根,负根,不知道题目要考查什么.这道题目放在这里的原因:跟上一道题的其中一种解法比较类似.
2.6 第3组题目
关于x的一元二次方程x2+(k2−4)x+k−1=0的两实根互为相反数,则k=___.
关于x的一元二次方程x2+(k2−4)x−1=0的两实根互为相反数,则k=___.
学生梁凯翔、袁华驹的板书

图1
周晔楠点评两道题目不一样的地方:c不相同
2.7 第4组题
在一次同学聚会时,参加这次聚会的同学共有x人,大家一见面就相互握手.
有人统计了一下,大家一共握了45次手,则方程可列为___.
在一次同学聚会时,参加这次聚会的同学共有x人,大家一见面就相互赠送了一件礼物
有人统计了一下,大家一共互赠了182件礼物,则方程可列为___.
选择这两道,除了学生得分率低,另外,主要想用具体的例子,让学生找到区分两种情景的方法,从而降低一些学生对于应用题的理解难度.提醒学生注意理解应用题的情景.
2.8 展示学生做对的题目所采用的不同解法.
2.8.1 让学生小结题目的方法:周晔楠,谢雅岚,何樱莉.

图2
2.8.2 让学生找错,被问的林依靖、黄许哲正是错题的主人.

图3
2.9 让学生感受不同解法的理解,被提问的王炜彬正是列式较繁杂的主人.

图4
2.10 让学生学习优秀同学的做法.
3 点评:亮点与困惑
1亮点
1.1教学行为重视细节
1.1.1评
比一般的直接讲题的试卷讲评课,点评的力度较大.先是面上点评,再分组表扬,具体到个人.也就是在这个环节中,笔者发现有一些第一次考得不理想但第2次进步了的学生,听课的精神状态很好.
1.1.2展
让学生到黑板板书;把最优秀的几张试卷,把最好做法的解法凑成一张试卷,让学生学习;用打印幻灯片的形式,班内学生的典型错例展示,让学生找错;让学生点评.给学生充分的展示机会.
1.1.3点
本节课上所有被点到名字的学生,绝大部分都是事先通过查看他们的试卷,了解他们解题情况后,事先拟好的名单,主要是有针对性地通过了解这些学生的解题情况来了解讲评课的效果.同时,也希望学生能通过思考,感受到自己的进步.让我欣慰的是,尽管板书环节无法预设他们的解法,但这节课上因为有更多的思维碰撞,所以有了更好的生成.导:学法指导渗透在课堂中,从题目设计到教师小结,都围绕着引导学生学会类比地学.
1.2题组教学更有利于纠错
2困惑
2.1板书环节的时间较长,是否值得?
如何引导学生更好地从板书中收益.因为有些学生可能觉得最对就行了,不一定很重视看黑板.
2.2不同层次学生是否得到了发展?
每次评卷,最大的困恼就是会的学生已经会了,不会的,好像讲了还是不会.两次测试,有些学生成绩进步特别大,那说明了什么问题呢?题目有很大的局限性?还是学生对于熟悉题型的自信心会影响答题效率?
2.3试卷讲评课,是组织重要,还是如何讲题重要?
2.4如何评价一节试卷讲评课?
