巧用几何直观 促进有效建模

邱月华

（石狮市第三实验小学，福建 石狮 362700）

几何直观是利用图形描述几何或者其他数学问题、探索解决问题的思路、预测结果。在许多情况下，借助几何直观能把复杂的数学问题变得简明、形象，这对于以形象思维为主的小学生来说，显得极为重要。建模是小学基本数学思想之一，大量存在于学生的数学学习中，如何巧妙运用几何直观，帮助学生进行有效建模，是一个值得思考的问题。下面笔者将结合实例论述在建模的五个阶段中（抽象、推理、模型、融通、应用），发挥几何直观的作用，使学生的体验更加到位，模型的感悟更加深刻。

一、借几何直观简化信息，聚焦核心助抽象

学生的视野里更多的是熟悉的生活原型，教学往往也是从生活入手，让学生在观察、发现、比较、分析中逐渐接近数学本原，抽象成数学模型。而摒弃现实情境中无关数学、无关本质的因素，进行信息的简化处理，有助于学生更好地进行抽象。如在北师大版一年级上册教学《快乐的家园》时，让每个学生手上拿一个实物说一说：“我手上有1个苹果。”“我手上有1块橡皮擦。”“我手上有1根铅笔。”在学生充分表述基础上提出：“能否在几秒内把手中的实物画下来并表示出各自手上的1个物品？”有的学生拿着的是苹果，马上开心地说行；有的提着1个书包，显得很为难。此时便有聪明的学生提议要画1个〇表示1个书包，教师适时组织学生讨论，明白能用简单符号表示实物。这时，利用直观符号，抛却材质、形状、大小等物品的物理属性，简化成半抽象符号，帮助学生建立数字的模型。又如教学“明明有苹果15个，军军的个数是明明个数的2倍多5个，军军的苹果有多少个？”的问题解决时，常借助线段图表示题目的关键信息（如图1），简化题目信息量，助推学生的进一步抽象思考，是学生建立乘加模型的基础。

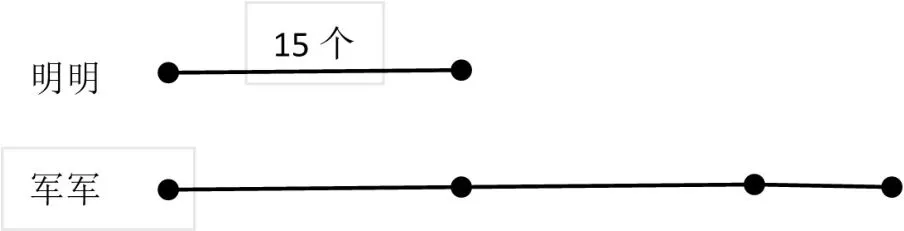
图1

二、借几何直观丰盈表象，辨析本质助推理

数学模型的建立，需要学生能透过现象发现数学本质，形成一般化的认识，这个过程需要提供丰富、变式的素材，让学生在观察与推理中建模。利用几何直观能为学生提供多种表征或多种不同思路，契合学生认知特点，有助于学生在辨析中进行逻辑推理，发现数学本质。如在“千以内数认识”的教学中，为帮助学生建立十进位值的模型，可以让学生用多种表征来体现235这个数字。学生不约而同地采用多种直观学具进行表达（如图2），在丰富的直观表征中，教师通过递进的问题串：1.仔细观察上面几种表示方法，有什么相同与不同？2.百位、十位、个位上一个珠子有什么不同？（揭示：不同位上表示珠子不同，个位上表示1个一、十位上表示1个十、百位上表示1个百）3.数字表示的235上的每个数字表示的含义是什么？这些问题引导学生进行逻辑推理，沟通不同几何直观之间的联系，在推理中完成十进位值模型的建构。

图2

三、借几何直观发现规律，符号表达助建模

数学的规律常常是在直观的表达中看出来的，而后再进行严谨的逻辑证明。借助几何直观的方式来解决问题，能让学生更迅速寻找到正确的思考方向，产生数学直觉，进而在不断抽象的符号表达中实现建模。如在教学“能被2和5整除的数特征”时，打破从观察数字特点入手的常规做法，放手让学生通过画一画的方式，判断46、127能否被2整除。学生尝试解决，在直观图形的启迪下（如图3），发现最后影响结果的是个位上的数字。提出猜想：能否被2整除，就看个位上的数能不能被2整除？教师引导学生用半抽象的符号表示，进行推理（如图4），得出肯定的结论。最后，再拓延到“能被5整除的数的特征”的探究。

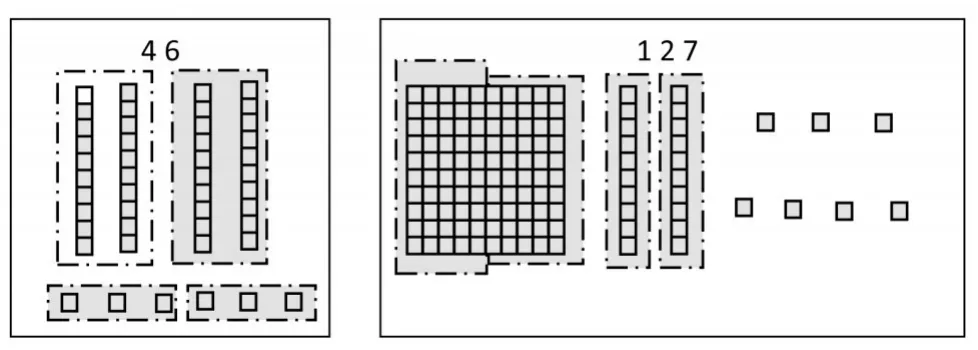
图3

图4

四、几何直观联结经验，阐释原理助融通

建立的数学模型要让学生真正内化通达，需要在建模的过程中阐释原理，让学生入其内而知其味，真正掌握模型的本质。几何直观的简明、形象性，能帮助学生快速实现经验的联结，感悟原理而实现知识的融会贯通。如教学“四舍五入”的近似值求法时，学生通过数据的观察及前期的建模，已经认识到求近似值时，要求精确到哪一位，就根据这一位后面的数值是否大于5进行求解，在方法与技能上学生的认识是到位的。但是从学生主要呈现的错例分析，可以发现学生对为什么取近似数时，只关注到指定数位的下一位，而忽略其他位数的情况，这一原理的感知是薄弱的，知其然而不知其所以然。基于这样的思考，设计一题让学生利用直观的数轴进行感知。1.请在下面的数轴上寻找到区分更接近30000或更接近40000的分界点（如图5）。学生迅速能找到是最正中的35000，以前的数更接近30000，以后的数更接近40000。2.在图6中找出更接近35000或更接近36000的分界点，学生找到两个数之间的35500。3.利用动态的放大镜，把图7中的刻度放大，请学生找出更接近35500或更接近35600的分界点，学生也正确找出35550这个分界点。让学生仔细观察3幅图，看看能发现什么？在直观的对比中，学生发现精确的程度越来越高，而每一次精确度的提高与下一个数位的中心分界点有关。此时，学生对求近似值时为什么要关注下一个数位的理解是到位的、连贯的，模型的建立才是丰盈的。

图5

图6

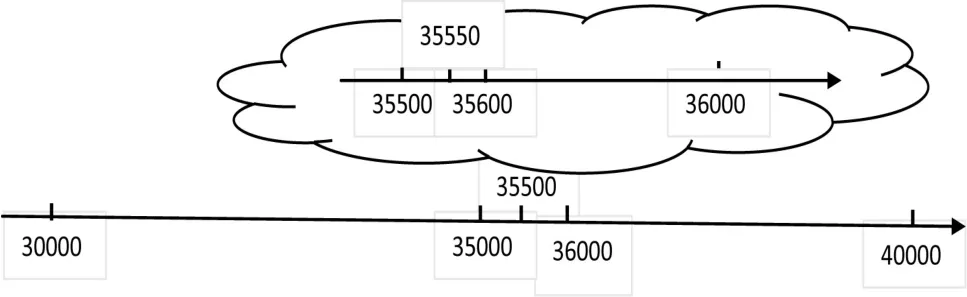
图7

五、借几何直观链接生活，把握本源助泛化

数学模型的建立从生活中来，回到生活中去。因其抽象性，每一个数学模型的生活原型较为多样，让学生真正把握本源，就要进行模型的实践应用。以几何直观的思考为载体，让学生进行联系生活的情境还原，有助于学生对模型本质的把握，感受模型应用的广泛性。如在学生构建完乘加的数学模型后，可以出示具有乘加运算结构的线段图（如图8），不附上任何情境信息，让学生自主去寻找生活的原型。学生提出多种不同的情境：1.每个布熊玩具50元，买3个布熊和一个30元的玩具鼓一共多少元；2.一个修路队每天修路50米，修了3天后剩下30米，这条路共长多少米；3.小汽车的速度是50千米/时，特快列车的速度是小汽车的3倍多30千米，特快列车的速度是多少千米；……深入分析学生还原的生活情境，可以发现有价格、修路、速度、长度等多个领域，有不同表述方式的情景再现，有进行信息转化的高维思考，这些多样化的表述都深化学生对乘加模型的认识，感悟到模型应用的广泛性，助推学生灵活通达的数学思维力的提升。

参考文献：

［1］冯崇和.几何直观：探索解决小学数学问题的重要手段［J］.内蒙古师范大学学报(教育科学版)，2014(8).

［2］黄伟星，顾晓华.培养几何直观能力的教学思考［J］.教育研究与评论(小学教育教学)，2011(6).