联合攻角约束视场角和落角的末制导律设计

曾耀华 谷永艳 李 娟

四川航天系统工程研究所，成都 610100

传统的比例导引律结构形式简单、需测量少、弹道特性好且制导精度高，在工程上得到了广泛应用。为了更好地发挥精确制导武器(如反坦克导弹)摧毁目标效能，要求能以期望的落角较小的攻角击中目标，而采用传统的比例导引律末端落角基本上已由初始制导视线角大小决定，不能主动控制落角使得传统比例导引律在该类武器中越来越难以适应。因此，出现了最早由Kim研究的偏置比例导引律(BPNG)[1]，通过在传统比例导引律基础上加上一个与落角偏差有关的偏置项构成。此后，随着越来越多的武器要求具有规定落角进行攻击，又出现了多种不同形式的带落角约束导引律[2-3]，其中比较典型的一类变系数比例导引律如文献[4]中描述，其形式类似BPNG，可看作是变系数的BPNG，其不需估计剩余时间而能达到期望落角约束。但该方法有适用局限，验证表明很多情况下难以达到需要的高制导精度。其他比较好的导引律如滑模导引律[5-6]，通过引入滑模变结构控制，提高落角约束项对测量或估计误差的鲁棒性。在带有偏置项的比例导引律中，由于偏置项的存在，可能会出现过大的视场角导致导引头丢失跟踪目标，因此还需要对视场角进行约束。文献[7]提出了一种开关逻辑型视场角约束方法，当视场角达到约束阈值时加入一个与视场角有关的约束偏置项，否则撤销该约束偏置项，通过设置合适的系数，可以平稳调节偏置项大小、平稳约束视场角在规定范围内。

任何的导引律其制导精度必须优先保证，由于传统的比例导引律具有高制导精度，因此文中以传统比例导引律为基础，借鉴偏置比例导引(BPNG)思想，基于滑模变结构控制的强鲁棒性，分析可见带落角约束的滑模导引律总体上为类偏置比例导引律形式，故设计了以比例导引为基本项，加上其他约束偏置项的结构构型为主要形式的末制导律。该末制导律在带重力补偿的传统比例导引律基础上，加入基于变参数滑模调节项和视线偏差比例项组成的落角约束变结构偏置项。同时，为约束导引头视场角超限，使该偏置项乘上一个指数形式的视场角约束带通型系数；为约束攻角过大，根据气动参数计算允许极限攻角对应的极限过载，把偏置项值限制在该极限过载内。最后，与最优系数BPNG方法通过对比仿真进行了验证。

1 多约束末制导律

1.1 落角约束末制导律

按照质点运动假设，建立俯仰平面内的弹目相对运动关系如图1所示。图中，M为导弹，T为目标，MT距离为弹目距r，MT连线为视线，视线倾角为q；导弹运动参数主要考虑弹道倾角θm、速度vm、速度相对视线的偏离角ηm=q-θm以及改变速度矢量方向的法向加速度控制量ac；目标运动参数主要考虑速度倾角θt、速度vt和速度相对视线的偏离角ηt=q-θt。

图1 弹目相对运动关系

建立弹目相对运动方程：

(1)

基于以上关系，根据零化弹-目视线角速率的准平行接近原理[4]，给定终点时刻tf的期望导弹终点弹道倾角θm(tf)，预测预估目标终点速度倾角θt(tf)，对于地面目标，一般可认为θt(tf)≈0。按照下式计算期望视线倾角λD为：

(2)

根据偏置比例导引原理[1]，参考滑模变结构制导律思想[5-6]，考虑重力补偿，本文提出带落角约束的末制导律形式如下：

(3)

式中，第1项为传统的比例导引，第2项为偏置项，第3项为滑模变结构项，最后一项为重力补偿项；N为导航比，kq和kg均为正的系数。

重写式(3)，表示为以下2项之和：

(4)

其中，aycsv为考虑重力补偿的传统比例导引项；aycsb为考虑落角约束的变结构偏置项，其由2部分组成：与视线偏差变化率有关的比例项和滑模调节项。

定义落角偏差变化率表示为：

(5)

其中，剩余时间采用如下估算公式[8]：

(6)

滑模项的存在，能够弱化剩余时间估计不准导致的大脱靶量。选取的滑模面切换函数为：

(7)

式中，k1>0，k2>0。

选取的滑模趋近律为：

(8)

式中，k>0，μ>0。

饱和函数形式为：

sat(S,δ)=S/|S|+δ

(9)

式中，饱和因子δ>0，δ越大，趋近饱和越平缓。

对滑模趋近调节系数ε设计为自适应变参数形式，其取值为与视线角速度有关的量，在末端能够保证获得最佳的脱靶量和较小的攻角，如下：

(10)

式中，系数ks>0。

1.2 落角偏差变化率约束

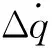
(11)

Ay1(·)函数表达为弹体系下的攻角对应的有舵偏时的法向加速度值，根据导弹动力学模型，给定时刻t导弹在某一攻角下所受的垂直弹轴的法向加速度可用下式近似计算：

(12)

(13)

然后乘以指数形式系数进行平滑过渡：

(14)

1.3 联合攻角和视场角约束

根据比例导引原理，传统比例导引项aycsv具有零化视线角速度的作用效果，即随着导引制导控制的不断进行，弹目视线角速度具有趋于0的平衡态，同时使得导弹速度矢量指向趋向视线方向。相反，落角约束变结构偏置项aycsb具有破坏aycsv零化视线角速度的反作用，使得导弹速度矢量指向偏离视线方向。速度矢量指向趋向视线方向的同时也具有使弹轴指向趋向视线方向的效果，而速度矢量指向偏离视线方向的同时也使得弹轴指向偏离视线方向。弹轴指向偏离视线方向导致导引头框架角增大，因此，为防止导引头框架运动范围超限导致无法跟踪

目标，要求控制导引头框架角大小，约束弹轴指向严重偏离视线，即视场角约束。

对于具有偏航和俯仰运动的两轴伺服平台式导引头，根据导引头性能指标，给定导引头俯仰框架角极限范围：qb∈[qbmin,qbmax]。无论对于BTT还是STT控制方式，aycsb的存在，主要影响俯仰框架方向，因此，只考虑俯仰框架角的约束。本文采用改进的框架角约束方式[7]，约束项作为系数用于调整aycsb的值，即aycsb乘以视场角约束带通型系数。该系数采用指数形式表示为：

kqb=(1-e-57.3τq(qb-qbmin))(1-e-57.3τq(qbmax-qb))

(15)

式中，τq为正的时间常数;kqb为约束项系数，且若kqb<0，则令kqb=0。

根据文献[7]的思想，可以设定一个阈值作为约束项系数起作用的缓冲区，即若满足

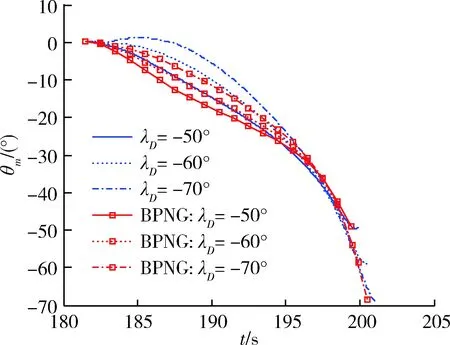
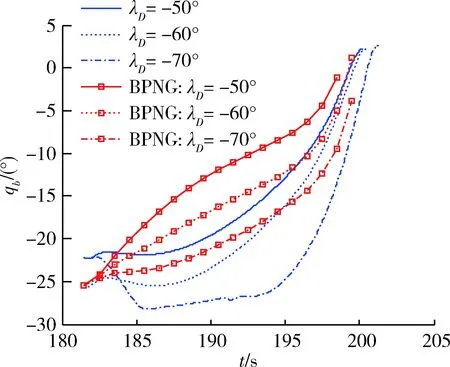
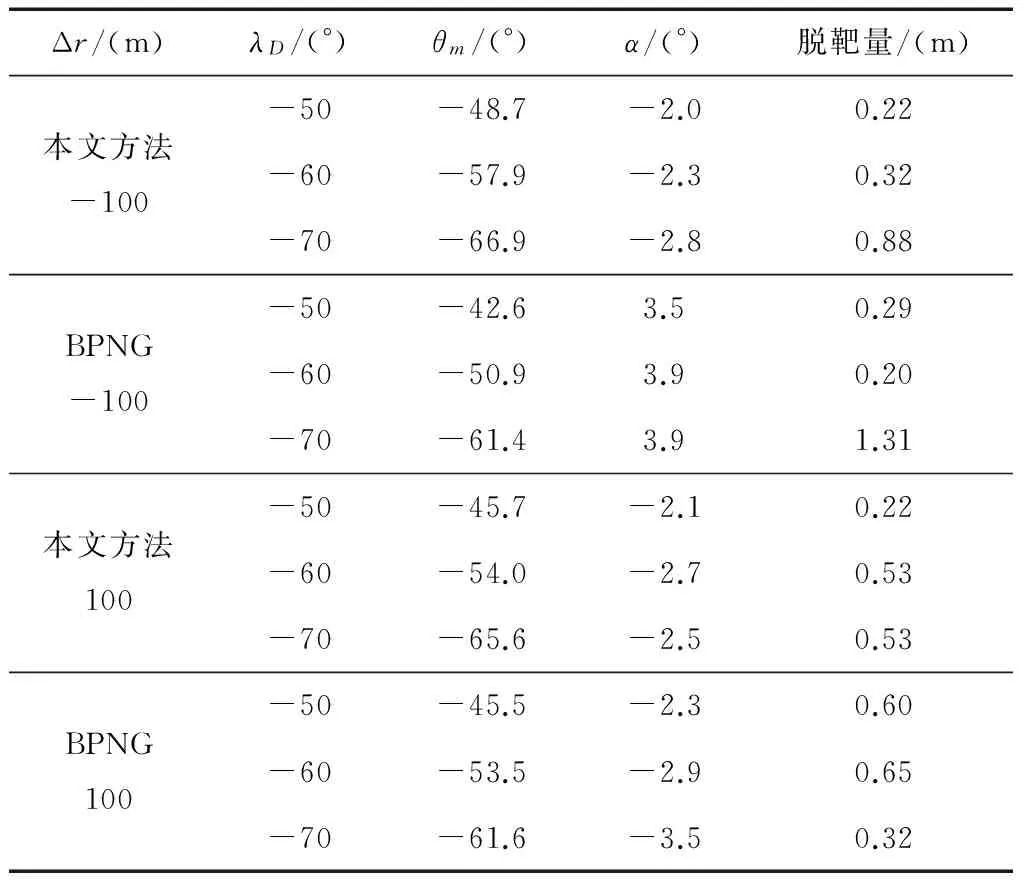
qbmin+Δη

(16)

则令kqb=1，其中Δη为正的框架角缓冲区宽度。

最后，根据允许极限攻角要求，对aycsb进行攻角约束。要求约束满足如下不等式

(17)

即

(18)

其中，

(19)

式中，舵偏上标“1”表示上一周期的值。

(20)

2 仿真分析

以某小型攻击巡飞弹末制导攻击目标为例，应用本文设计的多约束末制导律进行数学仿真分析，同时使用偏置比例导引律(BPNG)进行对比仿真，其形式如下：

(21)

该巡飞弹以平飞巡航方式进行侦察，发现待攻击目标后，导引头锁定目标，巡飞弹转入大落角导引攻击末制导。巡飞弹锁定目标时速度为30m/s，飞行高度为300m，锁定目标时刻弹目距离800m。设置参数N=3，kq=2，ks=3，要求飞行攻角范围α∈[-6°,12°]，导引头俯仰框架角范围qb∈[-30°,16°]，缓冲区宽度Δη=3。

不考虑弹目距离估计偏差进行仿真，即Δr=0，2种导引方法仿真结果比对见表1，从表中可见2种方法落角与期望值的偏差、脱靶量基本相当，但本文方法的落点攻角比BPNG的小。图2～4为相应仿真曲线，其中从图4可见，受视场角约束的作用，本文方法λD=-70°的仿真曲线表明俯仰框架角受到约束不至于超限。

表1 无弹目距离估计偏差仿真落点比对结果

图2 弹道倾角变化曲线

图3 攻角变化曲线

图4 俯仰框架角变化曲线

为检验弹目距离估计偏差对2种方法制导误差的影响，人为加入固定的正负弹目距离估计偏差进行仿真，即Δr=±100m，比对统计结果见表2，从表中数据可见，本文方法落角与期望值的偏差明显比BPNG小，正偏差时2种方法脱靶量基本相当，但当负偏差、大落角(-70°)时BPNG脱靶量出现超1.3m。可见，本文方法对弹目距离估计偏差有更强的鲁棒性。

表2 有弹目距离估计偏差仿真落点比对结果

3 结论

以要求对落角进行控制的目标攻击末制导律为核心设计对象，在带重力补偿的传统比例导引律基础上，设计了基于变参数滑模调节项和视线偏差比例项组成的落角约束变结构偏置项，构成了比例导引加偏置项形式的末制导律。滑模调节项采用变参数的滑模饱和函数，调节视线角速度和视线偏差占比分配，以达到既约束落角又保证制导精度。视线偏差比例项为视线偏差对剩余时间变化率成比例的乘积项，直接控制视线偏差趋向0。同时，考虑到偏置项可能导致导引头视场角超限和飞行攻角过大，设计了指数形式的视场角约束带通型系数，通过该系数乘上偏置项达到视场角约束的目的，合理调节系数时间常数以稳定控制，且可通过设置缓冲区来限制该系数起作用的范围。另外，根据气动参数计算允许极限攻角对应的极限过载，并把偏置项值限制在该极限过载内达到约束攻角的目的。通过对比仿真，验证了本文所提末制导律的有效性和鲁棒性，结果表明本文方法具有更小的落角偏差和末端攻角又不失高制导精度，对剩余时间估计误差容忍性更好，同时保证视场角不超限，有利于导引头持续跟踪目标。本文所设计的末制导律结构形式简单，需测量少，对估计误差不敏感，工程可实现。

[1] Kim B S, Lee J G, Han H S. Biased PNG Law for Impact with Angular Constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277-288.

[2] 张宽桥, 杨锁昌, 张凯. 带落角约束的导引律研究进展[J]. 飞航导弹, 2016, (7): 77-82. (Zhang Kuangqiao, Yang Suochang, Zhang Kai. Research Advances of Proportional Navigation Law with Impact Angle Constraint [J]. Aerodyn-amic Missile Journal, 2016, (7): 77-82.)

[3] 赵曜, 廖选平, 迟学谦, 等. 终端约束末制导律综述[J]. 航天控制, 2017, 35(2): 89-98. (Zhao Yao, Liao Xuanping, Chi Xueqian, et al. A Survey of Terminal Constrained Guidance Law [J]. Aerospace Control, 2017, 35(2): 89-98.)

[4] 覃天, 陈万春, 邢晓岚. 一种带落角约束的精确导引方法(英文)[J]. 宇航学报, 2012, 33(5): 570-576. (Tan Tian, Chen Wanchun, Xing Xiaolan. A Method for Precision Missile Guidance with Impact Attitude Angle Constraint [J]. Journal of Astronautics, 2012, 33(5): 570-576.)

[5] 张宽桥, 杨锁昌, 王刚. 带落角约束的有限时间收敛末制导律研究[J]. 弹道学报, 2015, 27(4): 30-36. (Zhang Kuanqiao, Yang Suochang, Wang Gang. Research of Finite-time Convergence Terminal Guidance Law with Impact Angle Constraint [J]. Journal of Ballistics, 2015, 27(4): 30-36.)

[6] 辛腾达, 范慧林, 王靖华, 等. 带落角约束的空地导弹滑模末制导律研究[J], 现代防御技术, 2016, 44(2): 86-91. (Xin Tengda, Fan Huiling, Wang Jinghua, et al. Sliding Mode Terminal Guidance Law for Air to Ground Missile with Impact Angle Constraint [J]. Modern Defence Technology, 2016, 44(2): 86-91.)

[7] 顾家立, 陈万春. 一种带导引头视角和落角约束的导引方法[J]. 宇航学报, 2013, 34(6): 782-787. (Gu Jiali, Chen Wanchun. Homing Guidance with Look Angle and Impact Angle Constraints [J]. Journal of Astronautics, 2013, 34(6): 782-787.)

[8] 张春妍, 宋建梅, 侯博, 等. 带落角和时间约束的网络化导弹协同制导律[J]. 兵工学报, 2016, 37(3): 431-438. (Zhang Chunyan, Song Jianmei, Hou Bo, et al. Cooperative Guidance Law with Impact Angle and Impact Time Constraints for Networked Missiles [J]. Acta Armamentarii, 2016, 37(3): 431-438.)