未知纬度下基于正交基构建的SINS直接解析对准方法

郑振宇 杨常青 唐 君

海军大连舰艇学院，大连 116018

捷联惯导初始对准是系统工作的基本前提，其核心任务是获取载体坐标系相对导航坐标系的姿态关系。近年来，捷联惯导初始对准已经形成了许多成熟的方法，如罗经对准法、基于最优估计的对准方法及基于矢量定姿的对准方法等[1-3]，诸多方法在应用过程中都需要精确的纬度信息支持。目前，纬度信息常来源于卫星或无线电定位手段，而对于水下、地下及密林等无线电信号无法覆盖的区域，获得纬度值并非易事，因此，研究未知纬度下的对准方法成为近年来初始对准研究的一个重要方向。

在静止基座下，捷联惯导自对准常采用解析式对准方法，该方法以地球自转角速度和重力矢量为基准，利用陀螺及加速度计观测解算姿态矩阵，该方法需要利用纬度信息建立地球自转角速度模型。为此，文献[4]提出了先利用地球自转矢量与重力矢量的角度关系估计纬度，再利用所估计纬度进行传统的解析对准方法，对准后不能保证姿态矩阵的正交性，需要进行正交化处理。本文从方向余弦矩阵的物理意义入手，提出直接利用加速度计、陀螺输出量构建标准正交基，最终建立姿态矩阵的对准方法，该方法未利用纬度信息，且不需要进行单独的正交化过程。对准实验表明该方法与已知纬度下的解析对准方法具有相同的精度，工程实用性较强。

1 未知纬度下传统解析对准方法

传统的解析式对准方法可表示为[5]：

(1)

(2)

由于2个矢量夹角与投影坐标系无关，因此，在静止基座下可根据以上角度关系估计纬度值[4]：

(3)

利用式(3)所求纬度仍可应用解析对准方法计算姿态阵，且纬度估计误差不影响对准精度。需要说明的是，采用式(1)得到的姿态矩阵并非正交矩阵，对准后需要进行正交化处理，常采用如下正交化处理方法[6]：

(4)

然而，在实际应用中，式(4)难以确保开方矩阵的正定性，工程上可采用如下迭代方法：

(5)

2 基于正交基构建的直接解析对准方法

2.1 方向余弦矩阵的正交基表示

解析对准方法本质上属于双矢量定姿的范畴，在数学上可以等效为利用线性无关向量组在2个坐标系下的坐标值求取坐标系之间的过渡矩阵。由于捷联惯导采用的坐标系均以(1,0,0)、(0,1,0)和(0,0,1)为标准正交基，因此，也可以直接利用观测量直接构建导航系正交基在载体系下的投影，该投影即为载体系到导航系的过渡矩阵。这种表示方式与方向余弦矩阵的物理意义是一致的，方向余弦矩阵的行向量正是导航系的轴向量在载体系的投影，如图1所示，姿态矩阵可以表示为：

(6)

其中，E，N，U分别为导航系x，y，z轴单位矢量在载体系下的投影，其中行向量元素代表该向量与载体系各轴向量的夹角余弦。

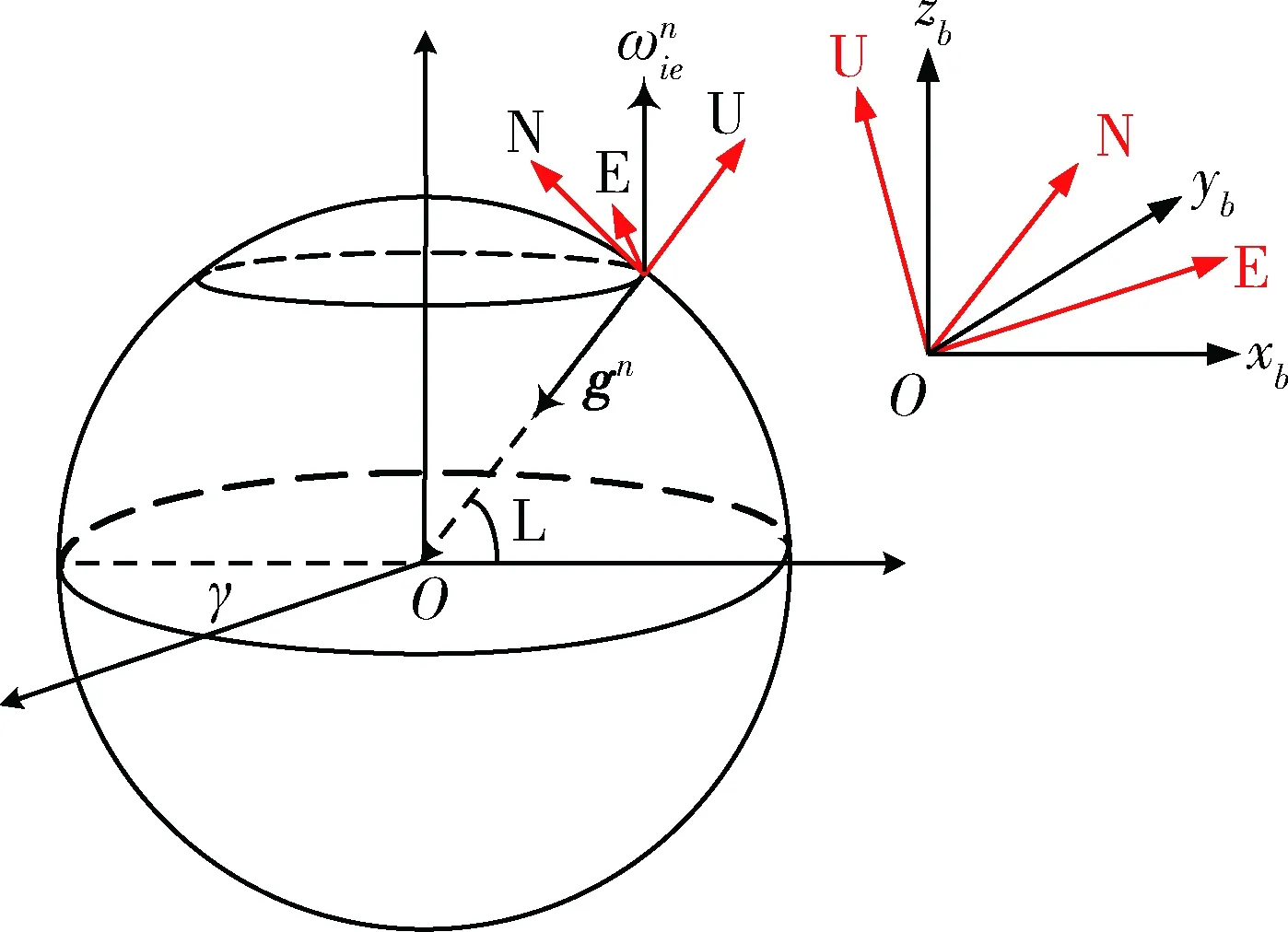
图1 方向余弦矩阵的正交基关系

2.2 直接解析对准方法

式(6)说明，只需求取导航系正交基在载体系的投影，即可确定姿态矩阵，该方法称为基于正交基构建的直接解析对准方法。由图1可以看出，在导航系下，“东北天”轴向标准正交基构成的单位阵可表示为：

(7)

其中，||表示对矢量取模。因此，静基座下载体坐标系下各轴向矢量的投影构成的姿态矩阵即可通过式(8)求取：

(8)

不难发现，式(8)仅利用了加速度与陀螺的观测矢量，无需纬度值。同时，各行向量均为单位向量且相互正交，无需再额外进行正交化处理，更具实用性。

2.3 与传统解析法的统一关系

式(1)中，M矩阵展开后可表示成：

(9)

将其代入式(1)可重新写为：

(10)

显然，矩阵M的作用有：1)矩阵N进行行变换；2)矩阵N行矢量取单位模。对比式(8)与(10)，不考虑误差条件下有：

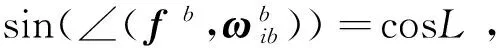
2.4 误差分析

(11)

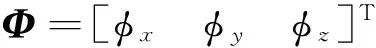
(12)

式中，▽b,εb分别为加速度计与陀螺的常值误差。根据式(11)有：

(13)

将式(12)其代入(13)，得到：

(14)

最终解算得到：

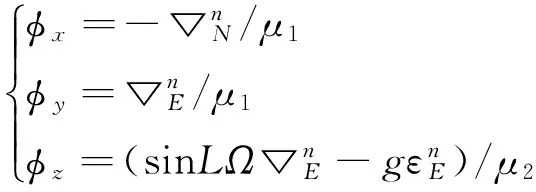
(15)

不考虑矢量模误差时，有μ1=g，μ2=gΩcosL。此时，式(15)与解析对准方法的对准误差关系式相同[8]。下面重点分析矢量模误差对精度的影响。以加速度计观测模为例，根据模解算关系：

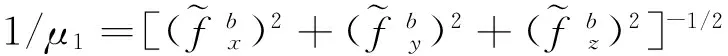
(16)

忽略误差二阶小量有：

对式(16)泰勒展开后可得：

1/μ1=[1-δfb/(2g2)]/g

(17)

以加速度计误差为1000μg为例，则δfb/(2g2)=0.001，矢量模误差形成的姿态误差为0.2″，显然，误差分析中可以忽略模观测误差的影响。另外，在IMU出厂前基本都需要进行矢量模标定，因此实际应用中可无需考虑矢量模误差的影响。

3 实验分析

3.1 仿真实验

仿真中设陀螺仪常值漂移为0.1(°)/h，随机漂移0.01(°)/h；加速度计零偏为1000μg，随机噪声为100μg；器件刻度系数误差均为50ppm，安装误差为5″。蒙特卡洛仿真次数设为100次，仿真步长设为0.01s，以静止基座100s的加速度计、陀螺数据为基础，采用平均滤波后分别采用式(1)与(8)的对准方法，对准解算误差统计结果如表1所示。从结果可发现，2种解析式的对准方法在精度上几乎没有差别，说明了在仿真中采用直接解析法时由常值误差和随机误差形成的模观测误差及纬度估计误差对精度影响十分微小，与误差分析结果是吻合的。

表1 2种解析式对准仿真实验精度比较

3.2 IMU数据解算实验

以自研光纤捷联惯导系统输出数据为仿真对象，系统采用陀螺的零偏稳定性优于为0.01(°)/h，加速度计零偏稳定性优于50μg。实验平台采用3KTD-565型三轴多功能转台，转台测角精度为3″，测角分辨率为0.36″，转台可实时输出台体真实姿态。实验采集时间为1h，静止状态下IMU输出数据，采用标定模型得到陀螺、加速度计标准单位输出，仍然选取100s数据的平均作为解算，进行20次对准解算，解算统计结果如表2所示。结果表明，实际系统中惯性器件误差特性虽较为复杂，但2种解析方法精度相当，因此，在实际工程应用中采用本文解算方法，无需纬度信息仍可获得同样的对准精度。

表2 2种解析式对准IMU数据解算精度对比

4 结论

在静止基座下可利用观测量直接建立东北天轴系在载体系下的投影，以此建立方向余弦矩阵，该方法是一种无需纬度支持的解析式对准方法，分析论证了该方法与传统解析对准方法在解析关系上的统一性，误差分析与实验均证明了该方法在精度上与传统方法是一致的，也表明了静基座下捷联惯导对准可不依赖纬度信息进行，且精度不受影响。

[1] 茹书山,赵忠华.基于逆向算法的捷联罗经快速对准技术研究[J].电子测量技术，2011,34(1):234-237.(Ru Shushan,Zhao Zhonghua.Study on Fast Alignmentmethod of Strapdown Gyrocompass Based on Converse Algorithm[J].Electronic Measurement Technology,2011,34(1): 234-237.)

[2] 高薪,卞鸿巍,傅中泽，等.捷联惯导晃动基座四元数估计对准算法[J].惯性技术学报，2014，22(6):724-728.(Gao Xin,Bian Hongwei,Fu Zhongze,et al.Alignment Algorithm Based on Quaternion Estimator for SINS on Rocking Base[J].Journal of Chinese Inertial Technology,2014,22(6):724-728.)

[3] Wu Y, Pan X. Optimization-based in-flight Alignment for Airborne INS/GPS Applications [C]://Proc.IGNSS Symp.Sydney, Australia,2011.

[4] 秦永元,严恭敏,顾冬晴,郑吉兵.摇摆基座上基于信息的捷联惯导粗对准研究[J].西北工业大学学报,2005,23(5):681-683.(Qin Yongyuan,Yan Gongmin,Gu Dongqing,Zheng Jibing. A Clever Way of SINS Coarse Alignment Despite Rocking Ship[J].Journal of Northwestern Polytechnical University，2005,23(5):681-683.)

[5] 陈令刚,刘建业,孙永荣,等.微小型捷联惯导系统解析式对准方法研究[J].航天控制, 2005, 23(4): 9-12. (Chen Linggang,Liu Jianye,Sun Yongrong， et al.Study of Analytic Coarse Alignment Methods to Micro SINS[J]. Aerospace Control,2005, 23(4): 9-12.)

[6] 严恭敏,严卫生,徐德民,等.纬度未知条件下捷联惯导系统初始对准分析[J].航天控制,2008,26(2):31-34. (Yan G M,Yan W S,Xu D M, et al.SINS Initial Aligment Analysis Under Geographic Latitude Uncertainty[J].Aerospace Control，2008，26(2):31-34.)

[7] 魏春岭,张洪钺.捷联惯导系统粗对准方法比较[J].航天控制,2000,18(3):16-21.(Wei Chunling,Zhang Hongyue.Comparison of Analytic Coarse Alignment Methods[J]. Aerospace Control, 2000,18(3):16-21.

[8] Error Analysis of Analytic Coarse Alignment Methods[J].IEEE Trans on Aerospace and Electronic Systems 1998,34(1):334-337.