电液伺服阀阀芯粘性阻尼系数辨识方法研究*

王书铭 蔡存坤 左哲清 延 皓 董立静

1.北京交通大学机械与电子控制工程学院，北京100044 2.北京精密机电控制设备研究所，北京100076

电液伺服系统在航空、航天、舰船、冶金和化工等领域中有着极为广泛的应用，具有结构紧凑、精度高和响应快[1-3]的优点。电液伺服阀作为电液伺服系统核心元件，可进行快速流量调节，在系统中起到了至关重要的作用[4-7]。由于工作可靠、性能稳定，滑阀一般被用作电液伺服阀的功率放大级。经多年研究，国内外学者已经建立了较为准确的滑阀模型，但由于液压系统中一些所谓的“软量”影响，模型中的一些参数较难确定[8-10]。这些“软量”包括阀芯粘性阻尼系数、液体弹性模量等。阀芯粘性阻尼系数反映了流体粘滞力与阀芯运动速度的关系，是滑阀模型中的重要组成部分，其大小与流体粘度、滑阀结构等有关，但至今仍未找到一种有效的理论计算方法或测试方法。所以，为建立滑阀的精确数学模型，乃至建立电液伺服阀的准确数学模型，需要寻求一种准确、有效的测试方法和辨识方法[11-18]，确定阀芯粘性阻尼系数的大小。

1 测试系统基本原理

粘性阻尼测试可以采用2种方法：1)从摩擦力与阀芯速度基本原理出发，结合合适的摩擦模型，拟合出粘性阻尼系数的静态测试方法[19]；2)利用振动系统模型辨识并计算出粘性阻尼系数的频率特性方法，即动态测试方法。

当阀芯行程较长的情况下，可采用静态测试方法，利用直线位移进给机构驱动阀芯作匀速运动，驱动杆上装有力传感器。根据牛顿力学运动定律，此时力传感器反馈值即为阀芯所受摩擦力，通过测定多个速度下的不同摩擦力值可拟合出阀芯所受摩擦力随速度变化曲线，从而可求出阀芯粘性阻尼系数σ。但阀芯行程较短时，静态测试方法所测试到的数据值往往误差较大，通用性不强，因而本文将采用动态测试方法，其动态测试基本原理如图1所示。

该测试系统主要由激振器、轻质弹簧、滑阀阀芯及激光位移传感器A与B组成，实物图如图2。

激振器输出位移信号，驱动质量-弹簧阻尼系统高频振荡。阀套右侧及激振器侧分别安装有一个激光传感器，将阀芯振动和激振器的位移信号通过数据采集卡采集进工控机。通过不同频率和幅值的位移指令信号，使得阀芯在不同频率下进行高频振动。通过采集的相应频率下的位移信号，绘制出系统幅频-相频特性曲线，计算机数据分析，拟合出系统的动态特性，从而得到系统的阻尼系数。

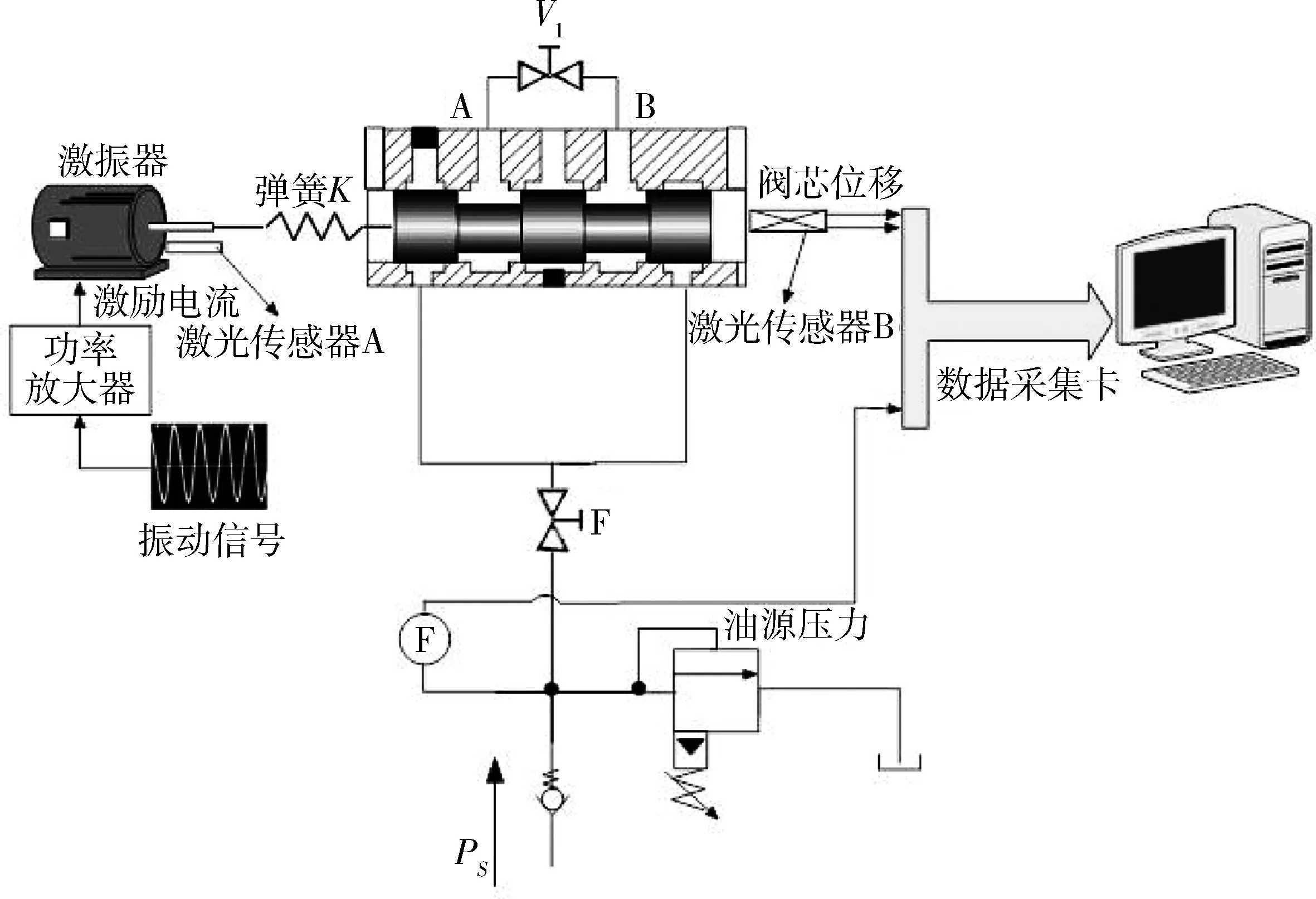
图1 粘性阻尼系数测试试验台原理图

图2 粘性阻尼系数测试试验台实物图

2 系统建模与辨识

2.1 粘性阻尼系统数学模型

通过对测试系统的结构分析，可以得到粘性阻尼系数测试系统的简化图，如图3所示。

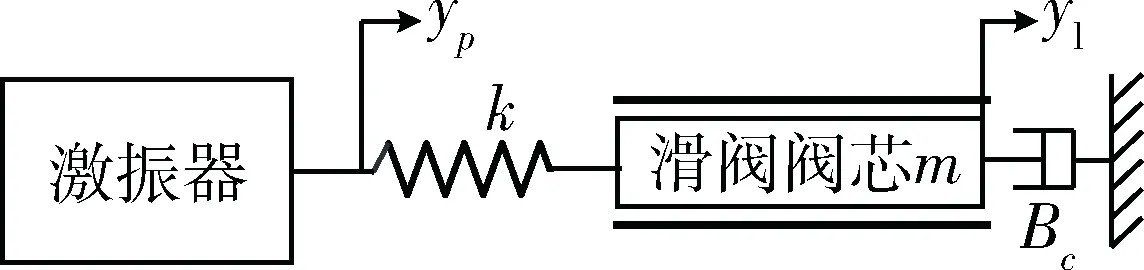
图3 粘性阻尼系数测试系统模型

其中，yp为激振器给定位移信号，即系统输入；yl为滑阀阀芯位移，即系统输出；k为连接弹簧的刚度；m为弹簧右端连接件质量+滑阀阀芯质量；Bc为滑阀粘性阻尼系数。

经过对滑阀阀芯的受力分析，且忽略库伦摩擦力非线性因素的影响，可得：

(1)

经拉氏变换后，得到系统的传递函数为：

(2)

通过传递函数，可以得到系统的固有频率ωn和阻尼比ε：

(3)

(4)

2.2 数据实时处理方法

对测控系统采集到的输入输出信号进行数据在线实时处理，可得频率特征曲线。

利用频率特性法，传递函数W(s)可以表示为：

W(jw)=A(w)ejφ(w)

(5)

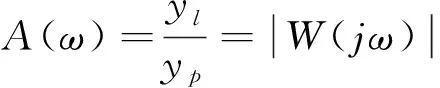
依据上述理论，位移传感器采集不同频率下系统的输入输出位移量，即可得到幅频特性曲线。

假设实测得到的正弦信号y(t)以一定频率f进行采样，需要辨识得到的信号形式为：

f(t)=vsin(wt+φ)

(6)

式中，v和φ分别代表信号的幅值及相位。其中幅值可通过工控机实时程序计算得到，w=2πf是已知的角频率。

取基函数φ0(t)=cos(wt)，φ1(t)=sin(wt)，式(6)可展开为：

f(t)=vsin(φ)cos(wt)+vcos(φ)sin(wt)
=A0φ0(t)+A1φ1(t)

(7)

式中，A0=vsin(φ)；A1=vcos(φ)，则

(8)

那么估计与实测的信号误差为：

Δ=f(t)-y(t)

(9)

建立优化方程：

(10)

式中，m为系统采样总数。这就将问题变成了线性极小化问题，根据上式分别对A0，A1求偏微分，得出：

(11)

对上式合并简化得：

(12)

(13)

那么，可以求出A0与A1，由式(8)可得到该估计信号的相位。

通过上述数据实时处理方法，可以求得该测试系统输入输出2个信号的相位差，进而得到该系统的相频特性。

2.3 系统传递函数辨识

根据试验得到的频率特征曲线，对其进行辨识，能够计算出系统的传递函数。

通过实验获得系统的实频特性Re(w)和虚频特性Im(w)，利用这些参数估计系统的传递函数。

设一个过程的传递函数为：

(14)

式中，n>m，对应的频率响应为：

(15)

而实测的频率特性数据为：

G*(jwi)=Re(wi)+jIm(wi)

(16)

在频率点wi上，估计与实测的频率响应误差为：

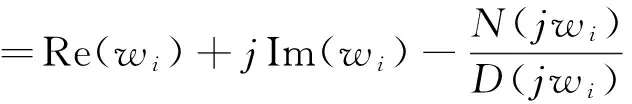
(17)

根据加权最小二乘法准则：

(18)

由式(17)和(18)，可以得出：

(19)

式中，

H(wi)=Re(wi)σ(wi)-Im(wi)τ(wi)-α(wi)

F(wi)=Re(wi)τ(wi)-Im(wi)σ(wi)-β(wi)

其中，

(a0=1,n=1,2，…)

(m=0,1,2，…)

即

(20)

解方程式便可求出传递函数的系数,从而可以得到系统的固有频率和阻尼比值，进而求出滑阀的粘性阻尼系数Bc。

3 实验过程及结果分析

针对某一型号的电液伺服阀滑阀，其阀芯质量m=0.0257kg，分别使用刚度K1=1.5N/mm和K2=1N/mm的2种轻质弹簧对其进行试验。该测试系统做扫频试验时，由上位机发出幅值为2mm的正弦指令信号，其初始频率设为1Hz，终止频率为50Hz，频率间隔为1Hz，每个频率点做10个周期往复运动。采样时间根据多媒体定时器取T=0.001s，对测试系统输入输出位移信号进行数据采集。通过采集的数据，利用第2.3节介绍的数据实时处理方法，可以得到系统的频率响应特性曲线，如图4所示。

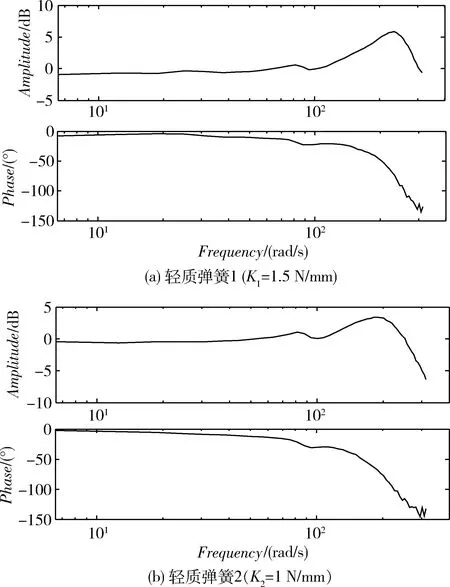
图4 实验所得幅频-相频曲线

再对所得实验曲线进行辨识，并将拟合出的系统幅频特性曲线与实验结果对比，如图5所示。

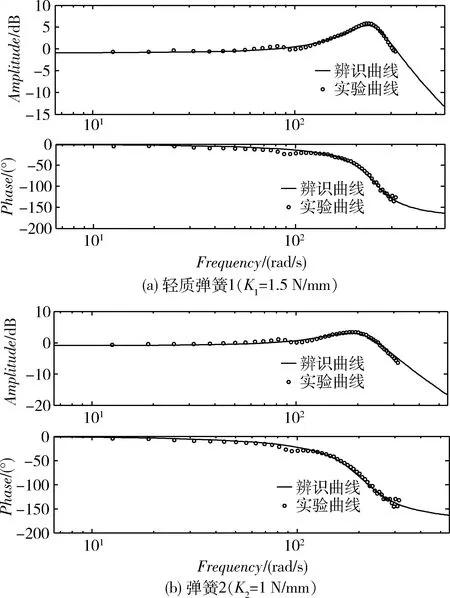
图5 辨识曲线与实验曲线对比图

根据图5的对比结果，可知辨识结果与实验所得数据基本吻合，验证了辨识方法的有效性。

相应的，根据此辨识结果可以得到轻质弹簧1及2系统的传递函数，其分别为：

(21)

(22)

据传递函数式(21)可以得到轻质弹簧1系统的固有频率ωn1=244.62rad/s以及阻尼比εz=0.25。根据传递函数式(22)可以得到轻质弹簧2系统的固有频率ωn2=210.35rad/s以及阻尼比ε2=0.314。由阻尼比ε，在已知阀芯质量和弹簧刚度的条件下，根据式(4)得到在不同弹簧刚度条件下测得的滑阀阀芯粘性阻尼系数分别为Bc1=3.11N/(m/s),Bc2=3.18N/(m/s)。从所得结果可以看出，在刚度为1.5N/mm和1N/mm的2种轻质弹簧试验条件下，得到的粘性阻尼系数的值基本一致，相差仅为2.25%，因此证明本测试方法是有效的、可靠的。

4 结论

阀芯粘性阻尼系数是电液伺服阀模型的重要组成部分。本文提出了一种基于加权最小二乘法准则的动态测试方法，能方便准确地辨识得到阀芯的粘性阻尼系数，为电液伺服阀的精确建模打下了坚实的基础。根据试验分析与辨识结果，主要结论如下：

1)将伺服阀阀芯看作一个二阶系统，通过测得其输入和输出，可直接得到系统粘性阻尼系数，且试验数据与理论推导相吻合；

2)利用加权最小二乘法辨识的数学方法，可准确得到系统的传递函数，这是推导粘性阻尼系数的有效方式；

3)在刚度为1.5N/mm和1N/mm的2种轻质弹簧试验条件下，得到的粘性阻尼系数值基本吻合，表明该动态测试和辨识方法可在较短的行程内较准确辨识出系统的粘性阻尼系数。

[1] Shang Yaoxing, Jiao Zongxia, Wang Xiaodong, et al. Study on Friction Torque Loading with an Electro-hydraulic Load Simulator [J]. Chinese Journal of Aeronautics, 2009, 22(6):691-699.

[2] 高炳微, 邵俊鹏, 韩桂华. 电液伺服系统位置和力模糊切换控制方法[J]. 电机与控制学报, 2014, 18(5):99-104. (Gao Bingwei, Shao Junpeng, Han Guihua. Fuzzy Switching Control Between Position and Force for Electro-Hydraulic Servo System [J]. Electric Machines and Control, 2014, 18(5):99-104.)

[3] Sangiah D K, Plummer A R, Bowen C R, et al. A Novel Piezo Hydraulic Aerospace Servovalve. Part 1: Design and Modelling [J]. Proceedings of The Institution of Mechanical Engineers Part I Journal of Systems & Control Engineering, 2013, 227(4):371-389.

[4] 康双琦, 江林秋. 电液伺服阀的发展历史及研究现状分析[J]. 资治文摘:管理版, 2009(5):194-194. (Kang Shuangqi, Jiang Linqiu. The Development History and Research Status Analyze of Electro-Hydraulic Servo Valve [J]. Views of Zizhi, 2009(5):194-194.)

[5] Sangiah D K, Plummer A R, Bowen C R, et al. Modelling and Experimental Validation of a Novel Piezo hydraulic Servo-valve [C]. ASME 2011 Dynamic Systems and Control Conference and Bath/ASME Symposium on Fluid Power and Motion Control. 2011:343-350.

[6] 陈彬, 易孟林. 电液伺服阀的研究现状和发展趋势[J]. 液压与气动, 2005,(6):5-8. (Chen Bin, Yi Menglin. The Present Research and Prospects of Electro-Hydraulic Servo Valve [J]. Chinese Hydraulics & Pneumatics, 2005, (6): 5-8.)

[7] 邹方晨, 郭栋. 电液伺服阀静动态性能测试台的设计[J]. 辽宁工业大学学报(自然科学版), 2016, 36(3):156-159. (Zou Fangchen, Guo Dong. Design of Static and Dynamic Performance Test Device for Electro-Hydraulic Servo Valve [J]. Journal of Liaoning University of Technology (Natural Science Edition), 2016, 36(3):156-159.)

[8] Shin W, Choi H, Shin H, et al. Development of a Direct Drive Servo Valve With Flow Force Compensated Spool [C]. Asme/jsme 2003, Joint Fluids Summer Engineering Conference. 2003:633-637.

[9] 水清皎. SM4-20双喷嘴挡板式电液伺服阀特性研究[D]. 兰州理工大学, 2013.(Shui Qingjiao. The Research of Characteristic O-n SM4-20 Twin Falapper-nozzle Servo Valve [D]. Lanzhou University of Technology, 2013: 62-90.)

[10] Pan X. Measurement of Spool Valve Overlap Value of Servo Valve [J]. Journal of Vibration Measurement & Diagnosis, 2009.

[11] Kadri M B. Comparison of Least Square Identification Schemes for a Model-Free Fuzzy Adaptive Controller [J]. Arabian Journal for Science & Engineering, 2014, 39(4):3067-3076.

[12] 宋涛, 于存贵. 基于MATLAB/Simulink液压伺服系统辨识仿真[J]. 液压与气动, 2015，(10):120-123. (Song Tao, Yu Cungui. Hydraulic Servo System Identification Simulation Based on MATLAB/Simulink [J]. Chinese Hydraulics & Pneumatics, 2015，(10):120-123.

[13] Wang D, Ding F. Input-output Data Filtering Based Recursive Least Squares Identification for CARARMA Systems [M]. Digital Signal Processing, 2010, 20(4): 991-999.

[14] 蒙杨超, 董自安, 王珂. 电液比例泵控马达系统辨识及实验分析研究[J]. 液压气动与密封, 2015，(3):35-40. (Meng Yangchao, Dong Zian, Wang Ke. Identification and Experimental Analysis of Electro-hydraulic Proportial Pump Control Motor System [J]. Hydraulics Pneumatics & Seals, 2015，(3):35-40.)

[15] 姚巍. 自行车机器人系统辨识及MATLAB仿真[D]. 北京邮电大学, 2008. (Yu Wei. System Identification and Simulation of Bicycle Robot [D]. Beijing University of Post and Telecommunication, 2008.)

[16] 于刚. 伺服阀控液压马达系统的辨识与控制研究[D]. 山东大学, 2007. (Yu Gang. Study on Identification and Control of Servovalve-Controlled Motor Control System [D]. Shandong University, 2007.)

[18] 田勇. 电液比例阀控马达液压系统辨识与恒功率控制策略研究[D]. 长安大学, 2014. (Tian Yong. The Identification of Electro-hydraulic Proportional Valve-controlled Motor System and The Study of Constant Power Control Strategy [D]. Chang’an University, 2014.)

[19] 弓萌野, 刘向东, 赖汝. 一种基于LabVIEW的新型阻尼测试系统设计[J]. 控制工程, 2012, 19(6):1206-1209. (Gong Mengye, Liu Xiangdong, Lai Ru. A Novel Damping Test System Based On LabVIEW [J]. Control Engineering. 2012, 19(6):1206-1209.)