一类具有预防控制的传染病模型研究

闫婷婷

（晋中职业技术学院，山西 晋中 030600）

传染病是人类疾病中不可避免且广泛存在的一种疾病，因其种类繁多危害性大且情况各异，所以人类对传染病的研究一直在深入且细化。通过数学模型对传染病的传播过程、病龄结构、预防控制进行细化分析研究，做出疾病控制的有效措施。

在辛京奇等文中基于经典的具有常数输入率和双线性传染率的SIR模型，建立一类具有接种的SIR-V传染病模型，得到了基本再生数，并证明了全局渐近稳定性[1]。杨亚莉等讨论了一类具有接种和因病死亡的SIS-V传染病模型的全局稳定性[2]。本文主要讨论一类具有预防接种的传染病模型，分析其平衡点的类型及无病平衡点和有病平衡点的全局稳定性。

1 模型的建立

如式（1）所示为一种具有预防接种的传染病模型，

其中S(t)表示t时刻易感染者数量，I(t)表示t时刻染病者数量，R(t)表示t时刻恢复者数量。N =S +I+R 表示总人口数量，a1表示出生率与死亡率的差值，a2表示染病率，a3表示接种率，a4表示恢复率。

引理1常数变量公式

2 系统的平衡点分析

定理1 总人口数量N是不变的。

证明 由于 N =S +I +R ，故有

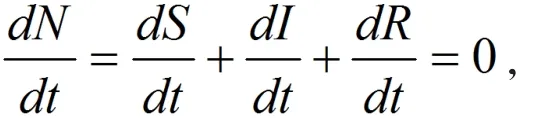
因此N是不变的，即 N= N0。

定理2系统（1）的解是有界的。

证明 因S(t)，I(t)，R(t)均表示人口数量，故S(t)，I(t)，R(t)≥0，又 N =S +I +R，再利用定理1知

系统（1）的平衡点应满足方程组

经计算，知（2）有两个解

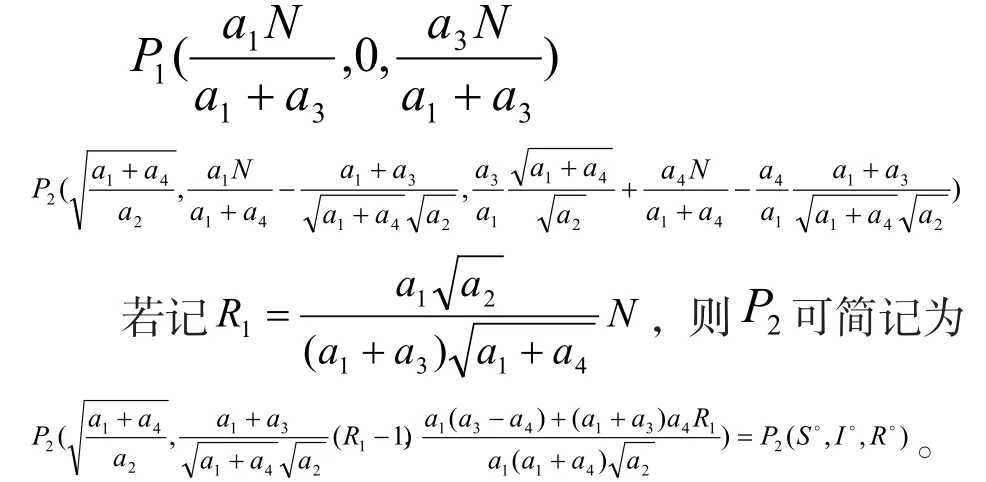
设P(S∗,I∗,R∗)为系统（1）的任意一个平衡点，则（1）在P处的线性近似系统的特征方程为

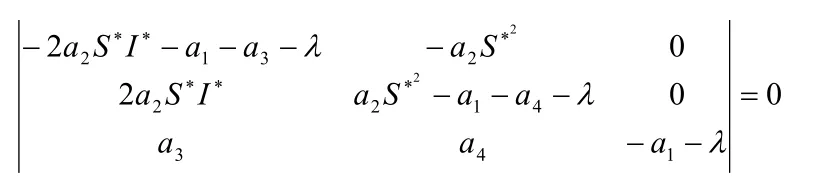
因此系统（1）在1P处的特征方程为：

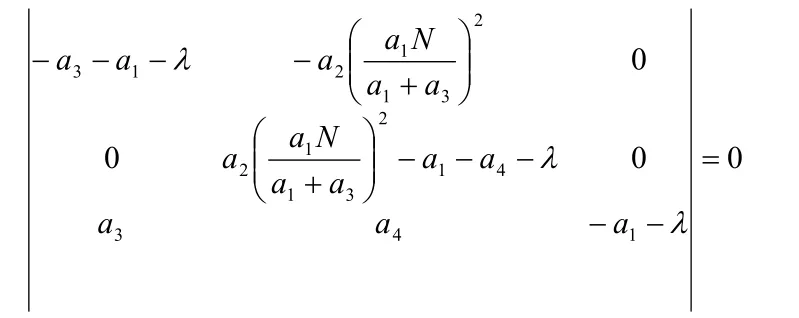
经计算解得

当 R1＜1时， λ2＜0，因此当 R1＜1时，为稳定的平衡点；

当 R1＞1时， λ2＞0，因此，当 R1＞1时，P1为不稳定的平衡点。

当 R1＞1，P2为正的平衡点，符合实际情况，系统（1）在P2点处的特征方程为;

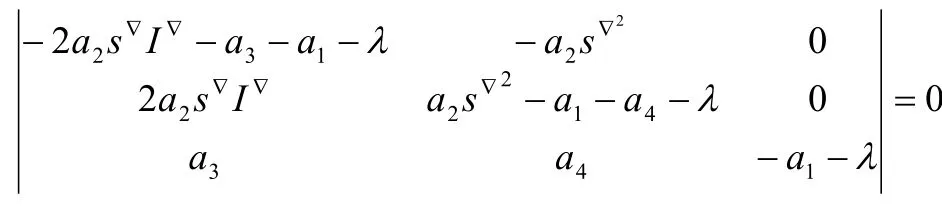
特征根 λ1=-a1＜0，剩下的两特征根应满足方程

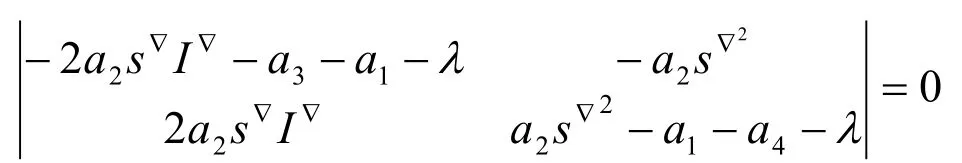
化简，得

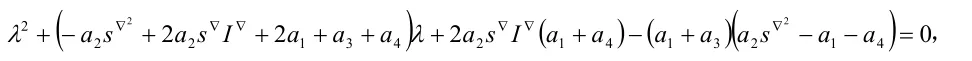
进一步化简，得

故由引理4知，P2为稳定的平衡点。

定理3 当 R1＜1时，系统（1）的平衡点 P1是稳定的；当 R1＞1时，平衡点 P1是不稳定的，但平衡点P2是稳定的。

3 平衡点的全局稳定性

定理4 当 R1＜1时，系统（1）的平衡点 P1是全局渐近稳定的。

由Bendixson判定知，系统（1）在G内无闭轨，又知当 R1＜1时，在G内只有一个平衡点 P1是稳定的，故 P1点是全局稳定的。

由于（1）中的两个方程不含R，故也可以考察（1）的前两个方程构成的子系统：

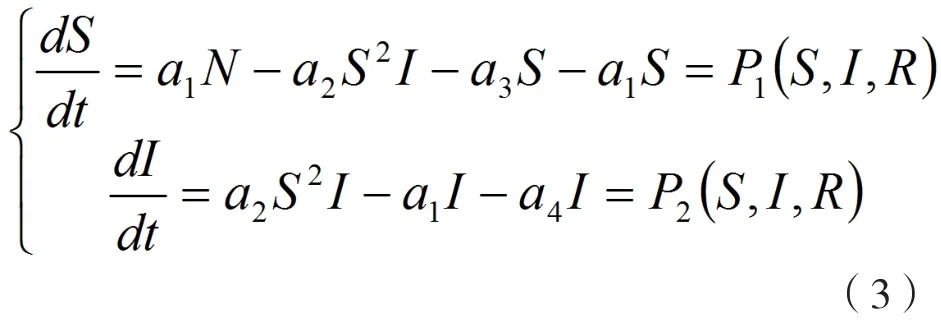
（3）的平衡点应满足方程组

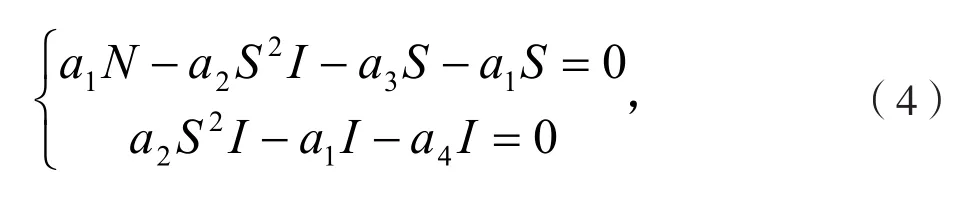
经计算知（4）有两个解

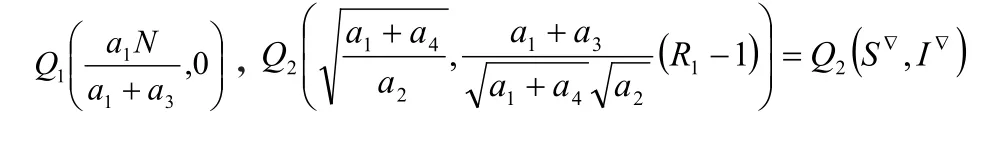
（3）在 Q (S∗,I∗)处的线性近似系统的特征方程为

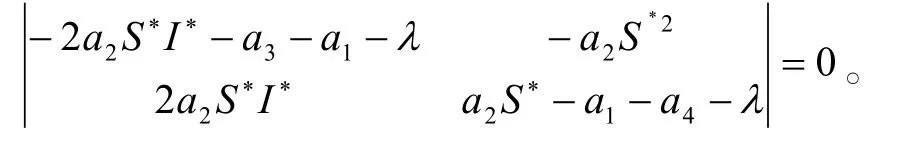
因此（3）在Q1处的特征方程为：

解得 λ1= -(a1+a3)＜ 0，

因此可见当 R1＜1时， λ2＜0，因此Q1为稳定的平衡点。当 R1＞1， λ2＞0，Q1为不稳定的平衡点。

系统（3）在Q2处的特征方程为

显然，从上式可以看出，当 R1＜1时，有特征根λ ＜0，故Q2为稳定的平衡点。

即有如下的结论：

定理5 当 R1＜1时，（3）的平衡点Q1是稳定的；当 R1＞1时，Q1是不稳定的，但Q2是稳定的。

定理6 对于系统（1）当 R1＜1时，有

证明 当 R1＜1时，Q1是全局稳定的，因此有

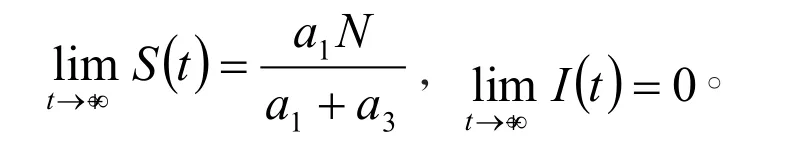
将上式代入系统（1）中，有如下的极限方程

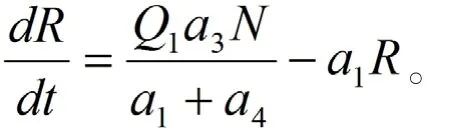
利用常数变量公式解得

又因R(0)=0，故C=0，即

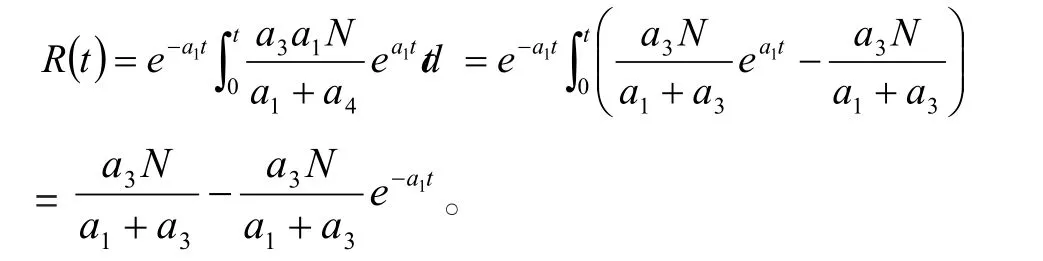
从上述分析可以看出，当 R1＜1时，该传染病根本不会传播开来。但 R1＞1时，该传染病将会流行开来，因此，需要通过降低R1的值来控制。

4 结论

本文主要讨论了一类具有预防接种的传染病模型，利用常数变量公式及Bandixson判定法进行了理论研究，分析了其平衡点类型，得到了无病平衡点和有病平衡点的全局稳定性。当基本再生指数小于1时，该传染病根本不会传播开来。但基本再生指数大于1时，该传染病将会流行开来，因此，需要通过降低R1的值来控制传染病的流行。

[1] 辛京奇，王文娟.一类带有接种的SIR传染病模型的全局分析[J].数学的实践与认识，2001,(20):71-76.

[2] 杨亚莉，李建全，张吉广.一类带有接种的传染病模型的全局性分析[J].西北大学学报，2009,(5):729-731+749.