巧用“对称关系”，妙求“最短路径”

☉江苏徐州市第十三中学 杨亚秋

在初中阶段，我们经常会碰到求线段之和最短、多边形的周长最小等类型的问题，面对这些问题，许多学生往往束手无策，一头雾水，究其原因，多半是平时不善于对所学知识、所做题型进行小结与反思.一旦学生平时缺少整理与反思，碰到问题时，自然会无据可依，无从下手.今天，我就和大家一起来谈谈最短路径问题中的一类简单问题的处理策略，以飨读者.

【问题背景】我们知道，当点A、B在直线l的异侧时，要在直线l上找点P，使得PA+PB值最小，只需连接AB，与直线l的交点P即为所求.那么，若点A、B在直线l的同侧，要在直线l上找点P，使得PA+PB值最小，我们又该如何处理呢？对于这种类型，可以找出A点关于直线l的对称点A′，连接A′B，与直线l交于点P，由对称性可知，PA′=PA，此时A′、P、B在同一直线上，PA+PB有最小值.

许多考题中都隐含了这种处理的策略，先来看一道函数题，如下：

【问题1】如图1，已知点P是抛物线y=-x2+2x+3的对称轴上的一个动点，抛物线与x轴交于A、B两点，与y轴交于C点，当PA+PC的值最小时，求P点的坐标.

【思路分析】由于A、B两点关于对称轴对称，所以可以利用二次函数的对称性，将线段PA转化成线段PB，这样当点C、P、B在一条直线上时，PA+PC有最小值.

【简析】根据抛物线的表达式y=-x2+2x+3，易求得点A（-1，0）、B（3，0）、C（0，3）.

因为A、B两点关于对称轴对称，所以PA=PB，如图2，故（PA+PC）min=（PB+PC）min.不难发现，当C、P、B在一条直线上时，（PB+PC）min=BC=3，此时直线BC的解析式为y=-x+3，与抛物线的对称轴直线x=1的交点为P（1，2）.

【点评】这是二次函数中典型的最短路径问题，解题时关键是要借助二次函数本身固有的对称性，将对称轴同侧的两定点转化到对称轴的异侧，这样问题就变得清晰、明朗了.

再来看一道几何题：

【问题2】如图3，正方形ABCD的边长为3，点E在边AB上，且BE=1.若点P在对角线BD上移动，则PA+PE的最小值是______.

【思路分析】A、E两点分布在直线DB的同侧.由于正方形关于其对角线成轴对称，所以可以借助A、C两点关于对角线DB对称，将线段PA转化成线段PC来解决.当点C、P、E在同一直线上时，PA+PE有最小值.

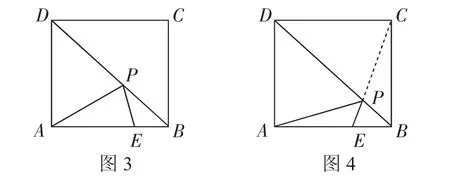
【简析】连接CE交DB于点P，连接PA，如图4.

由正方形的对称性，可知PA=PC，则（PA+PE）min=（PC+PE）min=EC=

【点评】遇到正方形这类本身就具有对称性的特殊图形，要仔细分析题设条件，挖掘图形中隐含的对称关系，发现其中蕴含的基本图形结构，从而顺利解题.

最后，我们一起来看一道中考题：

【考题再现】如图5，矩形ABCD中，AB=10，BC=5，点E、F、G、H分别在矩形ABCD各边上，且AE=CG，BF=DH，则四边形EFGH周长的最小值为______.

【思路分析】由AE=CG，BF=DH，易证得四边形EFGH为平行四边形.要求平行四边形EFGH周长的最小值，只要求得其周长的一半的最小值即可，即EF+FG的最小值.点E、G分布在直线BC的同一侧，求最小值问题，这就又回到了两点在直线的同侧，求线段之和最小值的基本问题上了.

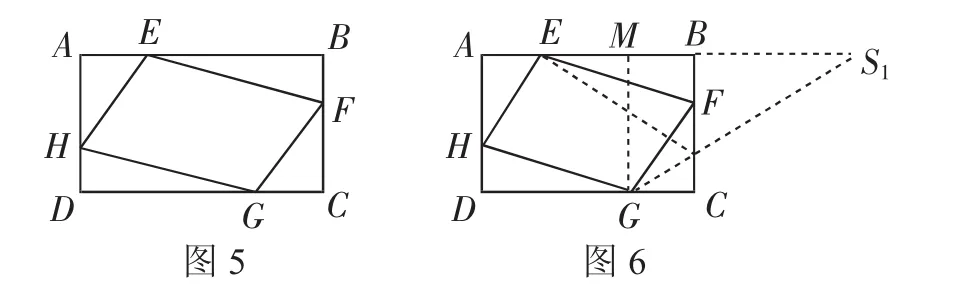
【简析】如图6，作E点关于BC的对称点E1，连接GE1，交BC于点K，连接KE，再过点G作GM⊥AB于点M.

由AE=CG，BE=BE1，得ME1=AB=10.

又GM=AD=5，则GE1=

则四边形EFGH周长的最小值为2E1G=10

【点评】此题是一道中考的中档题，由于定矩形中的平行四边形是个动平行四边形，这在一定程度上加大了此题的难度，仔细推敲后，我们可以发现，利用AE=CG及点E的对称点E1，总可以构造一个以矩形的长、宽为直角边的直角三角形，这样就可以求得斜边的长度，其实就是所求平行四边形的周长的一半.解决此题运用了“动中寻静”“变中探不变”的数学思想.

数学中的最短路径问题，对初中学生来说还是有一定困难的，其类型繁多，有时要利用图形中的对称关系，有时要对几何体进行侧面展开等.但是，只要我们掌握了其中一类问题的求解策略及解决问题的基本方法，那么再难、再复杂的最短路径问题，我们也可以将其化繁为简，将问题基本化.这就要求我们平时在学习数学时，要多总结、多反思，以不变应万变.W