CNC系统NURBS直接插补的应用研究

赵晓运，霍亚光，宋绪丁

（1.长安大学 道路施工技术与装备教育部重点实验室，西安 710064；2.台州学院 机械工程学院，台州 318000；3.长安大学 现代工程训练中心，西安 710064）

0 引言

在现代制造的数控加工领域，CNC系统NURBS直接插补技术，无论是在三轴还是在多轴系统加工中，都受到了广泛的重视和深入研究与发展[1～16]。随着社会和科学技术的进步，人们对各种各样产品的性能和外观等要求日益增高，对曲面设计尤其是复杂曲面已逐渐过渡到了用NURBS参数形式统一表示[16～20]。而伴随着数控加工过程的高速、高精和高效的要求，NURBS直接插补技术不仅日益凸显重要，而且是现代高端数控系统的一个重要发展方向[1,7,10～14]。CNC系统插补的实质是根据有限的输入信息，实时完成数据点的密化工作，从而使刀具按给定精度沿着规定的轨迹运动。插补技术是CNC系统的核心，各种轮廓加工均是通过插补技术来实现的。常规的CNC数控系统只包含直线插补和圆弧插补功能，对于复杂的不规则的曲面，一般由CAD/CAM系统生成符合精度要求的刀具路径，其实质是将加工对象离散成大量的直线或圆弧段，然后再将数据输入CNC系统，由数控系统执行直线插补或圆弧插补实现逼近加工。理论和经验证明[3,6～8,14]，采用基本的直线和圆弧插补方式，在面对非圆曲线曲面加工时，其主要不足有：加工质量和精度不高，程序量过大，加工效率偏低，因而不能适应现代工业高精、高速和高效的发展要求。为了弥补上述不足，人们研究发展了参数曲线直接插补方式[8,10,21～22]。在参数曲线中，样条曲线由于其良好的几何特性，受到了广泛的研究和发展。基于样条理论而发展起来的NURBS曲线，其特点是节点之间不等距，并用有理分式表达B样条曲线，吸纳了B样条曲线和贝齐尔曲线的几何形状特点，具有分段表示和整体连续等优良特性。目前，对于可以统一表达初等解析曲线和其它不规则的自由型曲线的NURBS曲线，由于其既可以较好地保留曲线的几何特性，又具有良好的操控性等，得到了较高的重视和发展。样条插补是指在数控程序编程时，采用参数曲线描述加工轨迹曲线，将包含曲线信息的数控加工程序输送至数控系统，由数控系统进行数据处理和曲线插补工作[14]。NURBS直接插补是基于样条插补的思想演化而来的，也就是说，在数控编程时，直接用NURBS曲线的描述参数进行数控加工轨迹描述，曲线的插补工作由数控装置直接计算完成，其实质是，基于参数变化，求出相邻两坐标之间的增量值，然后，通过坐标轴移动来实现插补折线，用于逼近目标曲线。NURBS插补可以使数控机床切削运动，严格按照理论NURBS曲线运动[4,23]，其主要优点有：加工精度高，刀轨光顺性好，程序量小，能适应高速、高精和高效加工等，其研究成果在不少高档数控机床上得到了应用。

本文基于NURBS基本理论，分析了NURBS插补的过程和实现方式，并通过实例，在所选定的机床上进行了加工测试，验证了NURBS插补方式的优良性，对工程编程实践具有指导意义。

1 NURBS曲线的参数表达

一条k次NURBS曲线可以表示为一分段的有理多项式矢函数：

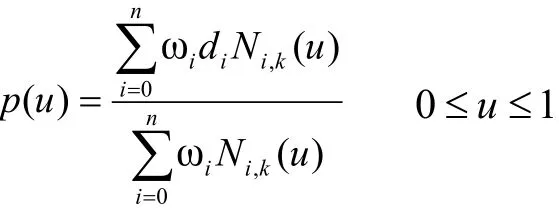
工程应用中多为已知型值点条件，要求根据型值点数据构建NURBS曲线，即曲线反求。在反求过程中，首先构造节点矢量，不同的参数化形式对节点矢量的构造有着较大的影响。常用的参数化形式[19，25]有：均匀参数化、积累弦长参数化、向心参数化和修正弦长参数化。当参数化和权因子确定后，NURBS曲线坐标值计算的关键核心问题是控制顶点的反求。控制顶点的反求，可以利用递推定义的递推公式，求出所有k次B样条的表达式，然后，再利用所选参数化形式所确定的参数值与型值点的对应值关系，列出矩阵方程，求出控制顶点。由B样条递推定义可知，随着曲线次数的升高，B样条计算的幂次也将上升，将给数值计算带来较严重的波动。实际应用中，常采用仿射变换直线段长度比不变原理所得到的矩阵表达式[18,25]计算控制顶点，该方法计算稳定，累积误差不敏感。

其中：

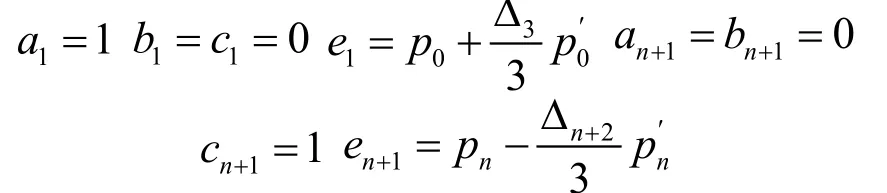
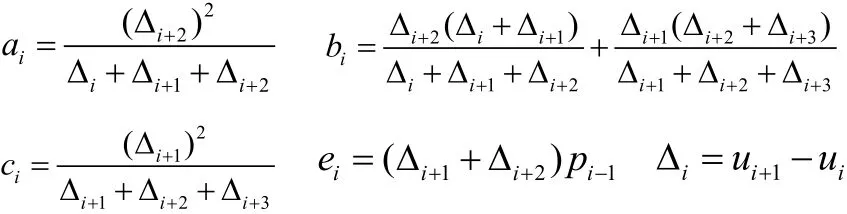
当节点矢量、权因子和控制顶点这三个参数完全确定下来之后，便可根据NURBS曲线方程表达式进行数据计算，并进行曲线插补工作。

2 NURBS曲线插补

根据NURBS曲线的理论知识可知，当曲线的阶次确定后，该NURBS曲线可由其节点矢量、权因子矢量和控制顶点三组基本参数唯一确定。数据点参数化形式，不仅决定了节点矢量的构建，也决定了控制顶点的反求和坐标点迭代运算的性质。NURBS曲线插补，就是根据当前插补点的参数，按照给定的条件，求出下一个插补点的参数，然后由NURBS曲线坐标方程，计算出下一个插补点坐标，进而由数控装置将坐标数据传送给驱动器，对机床进行运动控制，实现工件轮廓加工。

NURBS插补代码格式的特点是将NURBS曲线三个参数（节点矢量、权因子矢量和控制顶点）作为NC程序指令的组成部分。NURBS技术在CAD/CAM领域已经取得较为成熟的应用，但在CNC系统领域仍然相对滞后。常用的方法是，在CAD中采用NURBS曲线曲面构造出零件几何模型，然后在CAM中进行数控编程时，将零件的几何模型转化为含有NURBS插补代码的NC文件，最后，数控系统能够直接识别这些代码并进行NURBS插补运算。现行的三坐标NURBS插补指令，仍未形成统一的标准格式[10]。不少厂商如SIEMENS、FANUC等都开发出自己的带NURBS插补功能的CNC系统，但不同供应商的数控系统提供的NURBS插补指令G代码不尽相同，比较典型的G代码格式是，由G06.2作为NURBS插补开始的标志，数控装置读入三组NURBS刀心点数据，通过运算实现NURBS插补工作。本文选用现有的FANUC立式数控加工中心进行加工，其FANUC数控系统的NURBS插补功能代码格式如表1所

示[3,24]。

表1 FANUC18i-MB系统的NURBS插补G代码

通过NURBS直接插补，CNC系统可以精确控制机床实现NURBS曲线刀具轨迹的运动，从而克服由基本线型（直线或圆弧）插补而引起的插补技术误差。图1是NURBS刀具路径示意图。

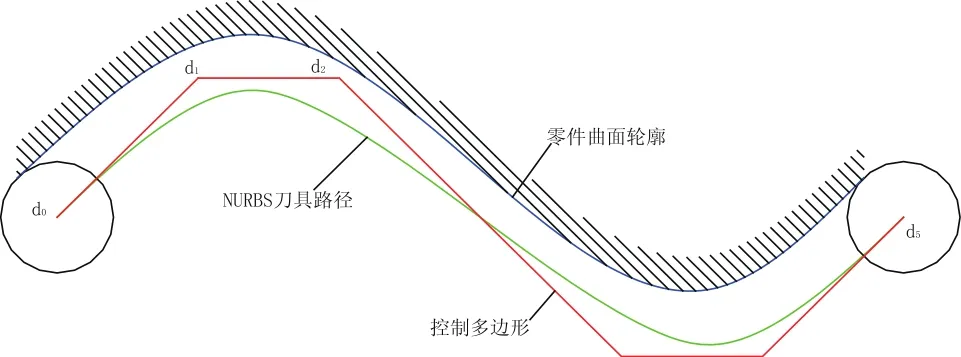
图1 NURBS刀具路径示意图

NURBS刀具路径是由CNC系统的NURBS插补器来实现内部的曲线运算，其主要优点体现在：可以减少数控加工代码的程序段数，提高系统对数据的处理能力；可避免直线插补时频繁的速度变化，缩短加工时间，适应高速加工；可以改善加工表面质量并提高加工表面的光顺性。

3 NURBS曲线插补实例

在自由曲面加工刀具路径规划中进行NURBS曲线拟合的主要任务是拟合已知的刀位点，将大量有序的刀位点直接拟合成NURBS曲线刀具路径，便可以直接传输给数控系统进行NURBS刀具路径的数控加工。这里，给定一组二维抛物线数据点如表2所示。

用插值法构造3次NURBS曲线，采用积累弦长参数化法构造出节点矢量为：

用曲线两端切矢条件构造补充方程，根据所给3次NURBS曲线控制顶点反求矩阵方程，求出控制顶点为：

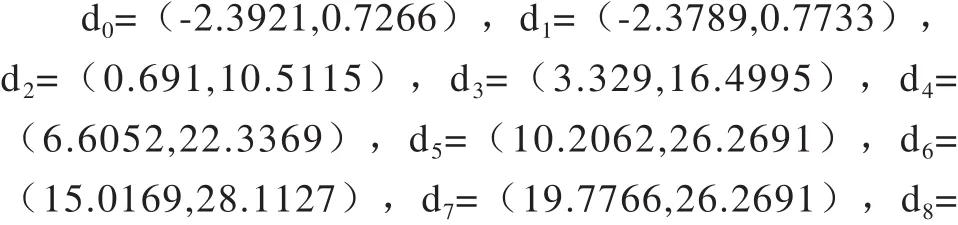
数据点理论曲线如图2所示。采用积累弦长参数化的插值曲线误差如图3所示。

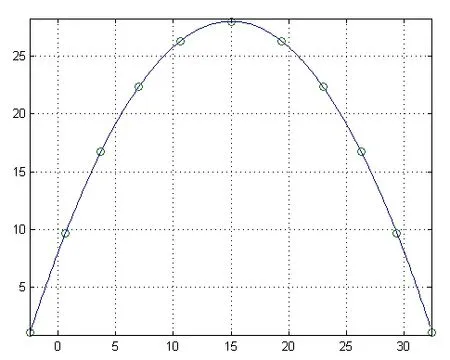
图2 数据点的理论曲线

图3 积累弦长参数化插值曲线误差

根据上述计算后得到的节点矢量和控制顶点，并取所有权因子为1，编写FANUC格式的NURBS数控代码如下：

表2 所给型值点数据

在商业软件上构建零件的三维模型如图4所示。选择FANUC 18i-MB数控系统的Hardinge/Bridgeport Vmc1000xp立式数控加工中心（如图5所示）进行铣削加工，定位精度为0.01mm，重复定位精度为：0.005 mm。分别采用直线插补、直线圆弧组合插补和NURBS插补方式进行加工，所得到的工件曲面如图6所示。

三种不同插补方式数控加工代码比较如表3所示。

表3 不同插补方式的数控代码

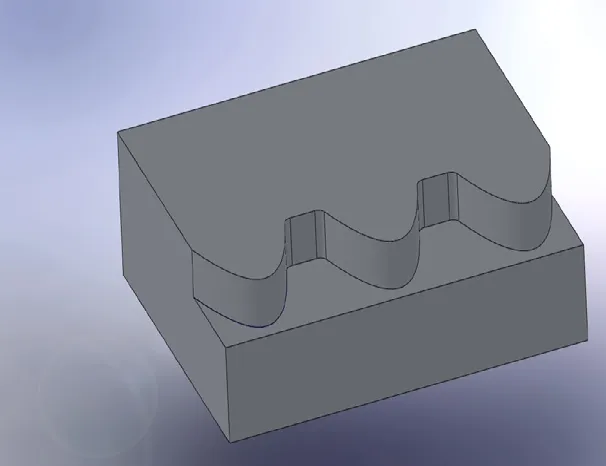
图4 工件的三维模型

图5 立式数控铣加工中心

图6 工件的加工曲面

在加工过程中发现，针对相同的刀位路线，采用直线插补，编程精度为0.01mm时，NC代码长度为213步；采用直线-圆弧插补，编程精度为0.01mm时，NC代码长度为592步；若要求更高的数控加工精度，则上述对应的数控加工NC代码的数量还会急剧增加。采用NURBS直接插补，程序段从G06.2指令开始，数控装置读取G06.2指令后面的三组数据进行插补计算，按NURBS曲线的定义直接实现NURBS插补，不需要近似插补所需的大量指令代码段。NURBS直接插补，程序段精简短小，与近似直线插补或直线圆弧插补相比，数控代码能减少50%至80%左右，大大地提高了效率和数控高速加工能力。

根据上述分析和图6可知，采用NURBS直接插补进行数控加工，不仅可以得到相对简洁的数控代码，而且还可以改善轮廓曲线光顺性，提高表面加工质量等。

4 结论

通过分析NURBS曲线的参数表达及其数据计算方法，研究了NURBS曲线插补过程及其数控代码格式。采用积累弦长参数化方式构造出给定数据的NURBS轮廓曲线，并编写出了其NURBS直接插补程序代码。通过加工实例，验证了NURBS插补的优良性。由实例可知，采用直线圆弧插补方式，数控加工的NC代码最长，592步；其次是采用直线插补方式的数控加工NC代码，213步；采用NURBS直接插补方式，其对应的数控加工NC代码最简练。结果表明：采用NURBS直接插补方式进行数控加工，数控加工NC代码精简短小，能适应高速加工，显著地提高加工效率和能力，具有较好的刀路光顺性和表面加工质量，对工程编程实践具有一定的指导意义。

[1]张小明,朱利民,丁汉,等.五轴加工刀具姿态球面NURBS曲线设计及优化 [J].机械工程学报,2010,46(17):140-144.

[2]黄翔,曾荣,岳伏军,等.NURBS插补技术在高速加工中的应用[J].南京航空航天大学学报,2002,4(1):82-85.

[3]刘萍,王民权,范进桢,等.FANUC系统中实时前瞻的NURBS插补研究与实现[J].机械科学与技术,2012,31(5):791-795.

[4]霍亚光,宋绪丁,刘海明.NURBS插补方式对数控铣削加工质量的影响[J].现代制造工程,2012,8:57-60.

[5]于志宏,陈刚.NURBS曲线插补理论与实践[J].制造技术与机床,2010,11:142-144.

[6]赵鸿,袁哲俊,卢泽生.NURBS曲线插补技术的应用[J].制造技术与机床,1999,12:44-46.

[7]张珲,徐宗俊,郭钢,等.CNC机床中的NURBS插补[J].制造技术与机床,1999,3:19-21.

[8]张永超,于洋,魏展鹏,等.自由曲面加工中NURBS曲线的插补实现[J].现代制造工程,2010,9:38-41.

[9]蔡善乐,张春政,石凯.反求NURBS曲线及其插补算法[J].新技术新工艺,2010,6:24-26.

[10]陈良骥,李慧莹.多轴加工曲线曲面实时插补理论与方法[M].郑州:郑州大学出版社,2016.

[11]陈良骥.复杂曲面数控加工相关技术[M].北京:知识产权出版社,2011.

[12]丁汉,朱利民.复杂曲面数字化制造的几何学理论与方法[M].北京:科学出版社,2011.

[13]于洋.五轴自由曲面NC加工刀路优化及误差控制[M].北京:国防工业出版社,2015.

[14]丁国富,江磊,朱绍维,等.五轴数控加工精度建模、分析及控制技术[M].北京:科学出版社,2016.

[15]解乃军,仲高艳.数控技术及应用[M].北京:科学出版社,2015.

[16]赵晓运,陈燕丽,宋绪丁.基于MATLAB和NURBS的叶片曲面造型[J].机械设计与制造工程,2016,26(2):22-26.

[17]Les Piegl, Wayne Tiller.The NURBS Book, 2nd ed[M].New York:Springer-Verlag,1997.

[18]Gerald Farin. Curves and Surfaces for Computer Aided Geometric Design,A Practical Guide, 2nd ed[M].Salt Lake City:Academic Press,1990.

[19]赵罡,穆国旺,王立柱.非均匀有理B样条[M].2版.北京:清华大学出版社,2010.

[20]陈燕丽,宋绪丁.基于B样条递推算法的NURBUS双四次曲面矩阵表示[J].制造业自动化,2014,36(2):90-93.

[21]桂贵生,何庆.高速加工机理与关键技术的研究进展[J].农业机械学报,2004,35(4):192-195.

[22]Bedi S, Ali I, Quan N.Advanced interpolation techniques for CNC machines[J].Journal of Engineering for Industry,Vol.115(3),1993:329-336.

[23]杨旭静,胡仲勋,钟志华.面向刀具路径生成的NURBS曲线拟合算法研究[J].中国机械工程,2009,20(8):984-987.

[24]杨旭静.自由曲面高性能数控加工刀具路径技术研究[D].长沙:湖南大学,2006.

[25]施法中.计算机辅助几何设计与非均匀有理B样条（修订版）CAGD&NURBS[M].北京:高等教育出版社,2013.