正交矩阵的性质初探

陕西省西安文理学院 樊 荣

一、正交矩阵的定义

定义1 一个n阶实矩阵A叫作正交矩阵， 如果AA'-A'A=E。

注：（1）一个n阶实矩阵A叫作正交矩阵， 如果A'=A-1。

（2）若n阶实矩阵A的n个行（列）向量是两两正交的单位向量，则为正交矩阵。

定义2 在n阶对角阵A中，若a11=a22=…ann=λ，λ∈R，则称此时的A为数量阵。记A=λE，其中E为n阶单位阵。

定义3 若n阶方阵A满足AT=A，其中AT为A的转置阵，则称A为对称阵。

定义5 若同阶A，B 方阵满足AB=BA=E，其中E为同阶单位阵，则称A与B互为逆方阵，记逆矩阵A-1=B或者B-1=A。

二、正交矩阵的性质

性质1 设A，B均为正交矩阵，则：（1）|A|=±1。（2）A'，A-1，A＊，AB 都是正交矩阵。

性质2 设A为正交矩阵，则其特征值的模等于1，且属于A的不同特征值的特征向量互相正交。

性质3 设A为正交矩阵，

（1）若|A|=-1，则A一定有特征值-1。

（2）若|A|=1， 且n为奇数，则A一定有特征值1。

性质4 设A是n阶正交矩阵，α是欧式空间Rn中的列向量，

性质6 （1）设A为对称正交矩阵，则A必为对合矩阵，从而A的特征值只能等于±1。

（2）设A为上（下）三角的正交矩阵，则A必为对角矩阵，且主对角线上的元素为±1。

性质7 设A为非对称的正交矩阵， 则A的特征值不可能全为实数。

性质8 设A为正交矩阵，

（1）若|A|=1，则A的任意子式与其代数余子式相等。

（2）若|A|=-1，则A的任意子式与其代数余子式仅差一个符号。

三、例题说明

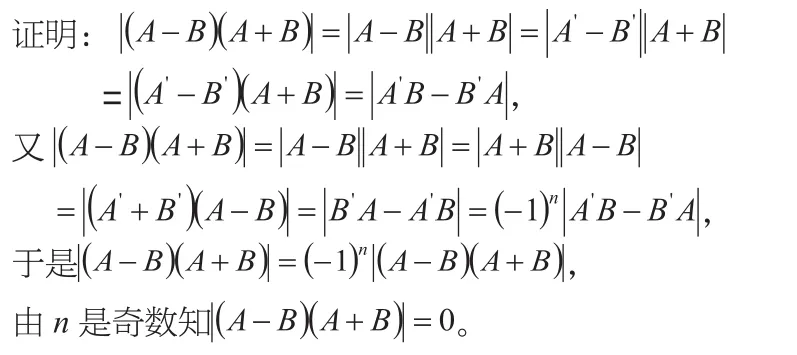
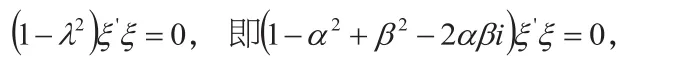
由性质2知α2+β2=1， 所以得

故x，y的模长相等且互相正交。

[1]张禾瑞，郝炳新.高等代数[M].北京：高等教育出版社，1983：321-328.

[2]戴立辉，王泽文，刘龙章.正交矩阵的若干性质[J].华东地质学院学报，2002，25（3）：267-269.

[3]郑艳林，刘少庆.关于正交矩阵特征值与行列式的两个定理[J].大学数学，2011，27（1）：161-163.

[4]吴险锋，张晓琳.正交矩阵的进一步探究[J].齐齐哈尔大学学报，2008，24（6）：65-68.