导学模式下高中数学高效课堂构建的探讨
2018-03-29江苏省泰兴市第三高级中学
江苏省泰兴市第三高级中学 陈 文
导学模式是一种高效的教学方法,该教学模式强调通过合理引导,让学生产生自主学习的意识,帮助其养成良好的学习习惯,培养学生创新思维能力,从而促进学生的全面发展。在新课改背景下,为保证数学教学达到相关目标,高中数学教师就应在课堂中实行导学模式,继而实现高效课堂的构建。
一、设计合理的预习学案,让学生做好学习准备
高效的课堂教学应从预习开始,预习不但是学习活动的开始,同时也是导学模式实施的重要环节。在预习阶段,学生若能够形成自觉主动的思维态势,可以让学生积极主动地参与到知识的探究与学习中,这样为学生迎接新的知识学习提供了巨大帮助。如在学习《直线与方程》时,课前预习阶段,教师就可以让学生思考如下问题:(1)倾斜角同斜率存在何种方式?(2)直线方程有五种形式,将各种形式的名称及对应的方程列出来;(3)两点间距离公式及运用。上述内容是《直线与方程》最基础的概念,如果学生不能够在预习阶段了解上述基本内容,实际学习起来就比较困难。学生在预习阶段通过解决上述问题,能够初步感受到直线与方程存在的联系,也正是在学生思考过程中,能够对预习过程中遇到的问题进行汇总,这样,教师实际上课的时候就可以通过提问的方式来获得具体的答案,这样的学习方式对学生掌握相关知识有重要的帮助。
预习阶段是导学模式的重点,主要是通过预习引导学生能够了解知识,让学生在思维上与心理上做好准备,同时充分培养学生自主学习与探究的积极性,让学生通过主动感知相关知识内容以达到提升学习效果的目的。
二、创设知识情境,激发学生学习兴趣
传统的高中数学教学中,教师常常会忽略课程讲解前的铺垫工作,往往单刀直入将本课堂的教学内容讲述给学生,这样学生很难对课程内容产生兴趣,这对高效课堂的构建不利。而在导学模式下,则要求教师需要关注主体课程教学之前的情境创设工作,通过情境引导学生进行相应知识的探究与思考,让学生产生深入了解知识的意愿。如《向量的概念与表示》的学习,该内容为入门课,概念比较多,教学内容比较枯燥,因而在实际教学中,教师可以创设如下情境:战国时期,有一个北方人要到位于南方的楚国。他从太行山脚出发,乘马车一直向北走,有人提醒他:“到楚国应该朝南走,你怎么往北呢?”他却说:“不要紧,我有一匹好马!”同学们猜猜结果这个人能够到达楚国吗?为什么?学生思考后立即回答到不了,因为方向错了。在学生回答后,教师就可以引入本节课主体内容“向量”的概念。
上述引导方式是通过情境创设激发学生的好奇心,让学生能够将思维与注意力转移到课程内容中,这样可以有效避免平铺直叙带来的生硬感。在课前导入阶段,通过问题引导,让学生在潜移默化中进入主体课程,这样可提高学生的积极性与主动性。
三、合理设置提问,引导学生深入理解知识
高中数学课堂教学中,教师不能一味地进行讲解,而是应通过在课堂中巧妙设置问题来激发学生思考,让课堂教学落实到解答老问题、发现新问题的良性循环中,培养与提升学生的主动思维能力。如学习《函数与方程》这一课时,教师可以提出如下问题:
问题一:确定如下方程根的个数:(1)3x+2=0;(2)x2-5x+6=0;(3)lnx+2x-6=0。探究方程的根与函数图象的联系。
问题二:函数y=f(x)的零点、方程f(x)=0的实数根、函数y=f(x)的图象与x轴交点横坐标,三者之间有什么关系?
问题三:零点个数一定是一个吗?试结合图形进行分析。
上述三个问题的难度不断递增,在几个问题的引导下,学生能够感受知识不断走向深入的节奏,这样可以让学生逐渐掌握相关知识内容,课堂教学质量不言而喻。
四、鼓励学生提炼总结,丰富思维拓宽知识
高中数学教学中,课后总结反思也是非常重要的环节。在教学结束后,引导学生进行反思与总结,可以让学生发现并且掌握规律性的思想方法,这样对学生进行难度更大、层级更高的学习与探究有重要帮助。如在《点、线、面之间的位置关系》的学习中,可以引导学生总结,并且探究如下问题:图1中,S为平行四边形ABCD外一点,M、N分别为SA、BD上的点,同时求证:MN∥平面SBC。
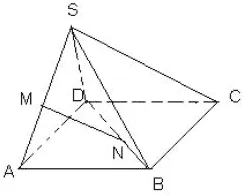
图1
上面这个习题整合了课程的基础内容,学生在求解这道题时,可以巩固课程相关知识,掌握知识运用方法,这对提升学生的数学综合水平有重要意义。
总之,在新课改背景下,高中数学教师可以使用导学模式引导学生预习、探究与理解,将学习的主动权交给学生,激发学生自主学习积极性,构建良好的课堂学习氛围,让学生能够真正将数学课本知识转变成自己的知识,提高学生的数学综合水平。
[1]李红叶.学案导学模式在高中数学教学中的实践研究[J].新校园,2016(02).
[2]白福明,吕玉娟.导学模式下的实效高中数学课堂初探[J].中学数学,2017(05).
