大跨钢桁拱桥局部杆件动力特性及涡振发生风速的影响因素研究

遆子龙， 李永乐， 徐昕宇

(西南交通大学 桥梁工程系，成都 610031)

钢桁拱桥具有外观雄伟、跨越能力大、承载能力高等优点，在现代桥梁建设中有较广泛的应用，如大宁河大桥[1]，南京大胜关长江大桥[2]，重庆朝天门大桥[3]。大跨度桥梁柔度较大，在强风的作用下，容易引发风致振动，影响桥梁的安全性与行车的舒适性，严重时会造成结构风致灾害，抗风性能已成为大跨度桥梁设计的控制性因素[4]。与斜拉桥、悬索桥等大跨桥梁相比，钢桁拱桥的刚度较大，整体抗风性能较好。但拱架局部杆件所用的箱型或H型等钝体断面杆件，因其长细比较大，在低风速下，当漩涡脱落频率与构件的固有频率接近时，持续不断的涡激力可能会导致涡激共振[5]。虽然涡激振动是限幅振动，但仍可能使局部杆件失稳或在杆件连接处产生疲劳损害。1973年，施工中的美国Commodore Barry三跨连续钢桁桥在强风作用下，导致9根H型杆件节点翼板处完全断裂。因此，针对大跨钢桁拱桥局部杆件的涡激振动性能开展研究十分必要。

结构的涡激振动发生风速与其自振频率密切相关，因此，准确计算局部杆件的自振频率对涡振发生风速的确定至关重要。Rudge等[6]对海洋导管架的局部杆件进行了涡振研究，指出局部杆件的约束条件是介于1(两端刚性约束)与0(两端铰接)之间，对于焊接，建议使用0.7的近似约束系数来计算自振频率。汪睿等[7]对导管架局部杆件动力特性进行了分析，并对杆件在不同约束系数下的自振频率进行了对比研究。张著名[8]对大跨钢桁桥的局部杆件进行了稳定性与风致振动的数值模拟与风洞试验研究，研究中杆件两端采用了固结的处理方式近似考虑。李晓猛[9]对集装箱起重机圆截面杆件风致振动进行了研究，计算了局部杆件在不同杆端约束下的自振频率，并对结果进行了讨论。邓洪洲等[10]对输电塔典型节点钢管杆件动力特性进行了研究，计算并比较了钢管杆件在不同节点板种类下的自振频率。

针对大跨钢桁拱桥局部杆件的风致振动问题，现有研究较少，且已有类似研究中，多将局部杆件的边界约束简化为固结，或简单的乘以经验的约束系数。钢桁拱桥局部杆件约束条件复杂，事实上，对于钢桁拱桥，杆端约束条件不仅只有三个杆端转动自由度的变化，还有三个平动自由度的变化。采用两端固结的约束条件与工程实际不符，通过经验公式笼统地取一个支撑系数的方法普适性与精度也较低。同时，考虑成桥荷载作用下刚度变化、杆件内力、节点板长度均会对杆件自振频率造成影响，不可忽略。

本文针对沿海某大跨度钢桁拱桥中长细比较大的箱型、H型两种断面杆件，通过有限元及计算流体力学的方法，研究了考虑全桥约束下杆件的涡激振动性能。使用“零密度”法进行局部杆件动力分析，考查了结构内力、节点板长度对杆件自振频率的影响，采用计算流体力学CFD(Computational Fluid Dynamics)的方法研究了两种钝体断面的气动特性，分析了局部杆件涡激振动性能的影响因素。

1 工程概况

某沿海地区中承式公路钢桁拱桥1/2桁拱立面布置图见图1(a)，主拱跨度较大，达424 m，全桥均采用钢结构。沿海地区常年受强季风、台风侵袭，结构抗风问题至关重要。在主拱圈端部附近，由于结构矢跨比设计需要，局部杆件长度较大，刚度下降，发生振动的可能性较高。同时，这些杆件断面均为箱型或H型等钝体，杆件整体气动性能较差。

以结构的长细比作为指标，选择典型的细长杆件。由材料力学长细比λ的定义

(1)

式中：I为惯性矩；A为截面面积；l为杆件长度，μ为与杆端约束有关的长度系数。假设所有杆件两端约束条件相似，系数均为μ1，对主拱圈端部附近较长杆件进行计算，确定了主拱圈端部附近两类典型长细比较大的杆件，编号为#1和#2，位置见图1(b)。#1、#2杆截面长度分别为23.8 m、19.3 m，断面参数见图1(c)，计算得其长细比分别为54.7μ1，124.3μ1。成桥状态下，#1、#2杆件各项参数见表1。

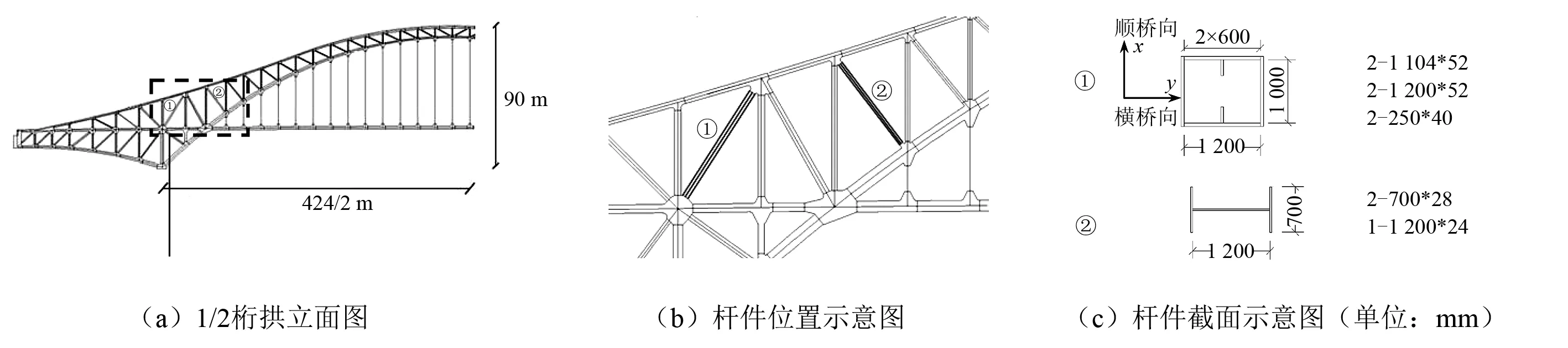
图1 全桥及截面示意图Fig.1 General layout of the bridge and local members

杆件A/m2Iy/m4Iz/m4内力/kN#10．2604．91×10-26．0×10-2-28840．1#20．0800．189×10-21．82×10-24118

2 局部杆件动力特性分析方法

2.1 常规分析方法

对于大跨钢桁拱桥局部杆件的动力特性问题，其边界条件的确定是重点和难点。以往对局部杆件的研究，边界约束主要采用两种方法：理想约束和经验公式法。张著名和李晓猛使用固结或铰接等典型理想约束对杆件的动力特性及风致响应进行了分析。Rudge等使用经验公式(2)对海洋工程中导管架结构的固有频率进行了计算

(2)

式中：φ为0～1，来表示边界条件从铰支到固结之间的变化系数，并建议使用φ=0.7。

事实上，在全桥约束下，杆端约束条件并非介于铰接与固结之间，杆端不仅有三个杆端弯曲自由度ROTx，ROTy，ROTz的位移，也有Ux，Uy，Uz的平动位移。采用两段铰接或固结的约束条件与实际结构不符。

在整体结构有限元模型上，也可进行局部杆件动力特性分析，但由于整体结构模态和局部杆件模态处在不同频段，加上整体结构自由度数量庞大，模态计算量过大，且局部杆件进行涡激振动分析所需的特定模态往往难以寻找。因此，需要寻找对局部杆件更合理的求解方法。

2.2 “零密度”法

对于大跨度钢桁架拱桥，局部杆件的振动有以下特点：

(1)局部杆件模态(高频)和整体结构模态(低频)不在同一个频段，整体模态和局部模态耦联效应很弱。

(2)杆件的涡激振动通常是基频控制，周边杆件振动的参与质量很有限。

基于以上两个前提，对于全桥结构中的局部杆件自振频率求解的问题，可以简化为求解局部杆件在全桥其他杆件约束下的动力特性的问题。此时，将全桥除目标杆件之外的其他结构看作理想钢架约束(即只有刚度没有质量)，对整个系统进行动力分析，这时：

(1)从结构力学的角度看，其他杆件的刚度与约束仍然不变，除目标杆件外的其余所有结构相当于一个理想的钢架，作为目标杆件的边界条件。此时求出的整个结构的自振频率也即目标杆件在整体结构约束下的自振频率。

(2)从结构动力学角度看，对于多自由度无阻尼自由振动方程，

(3)

结构的内力会影响结构刚度，从而影响结构动力特性。一般情况下，压力会使单元刚度减弱，从而减小自振频率，拉力反之。钢桁拱桥局部杆件以受轴力为主，内力对动力特性的影响不可忽略。但“零密度”法忽略了全桥质量，由重力产生的杆件内力无法直接获得。由于在有限元计算中，荷载均以单元节点力的形式施加，因此，可以通过施加重力等效节点力的方式来考虑内力对全桥刚度的影响。具体步骤如下：首先进行正常密度下的全桥建模(考虑所有质量)，然后将模型所有节点刚性约束，施加重力，并进行静力求解。提取静力结果中所有的节点力，即是重力等效节点力。将等效节点力按节点号再施加到“零密度”模型上，进行考虑重力引起的内力下的局部杆件动力求解。

进行钢桁架拱桥有限元建模时，桁架中杆件单元之间通常以共节点的方式直接连接，这在进行全桥动力特性求解时，是可以满足求解精度的[11]。但对于局部杆件，杆件的真实长度对自振频率影响显著，不可忽略。杆件之间是通过节点板相连的，节点板刚度明显大于杆件刚度[12]，因此，计算中将节点板按刚臂进行考虑，刚臂密度设为零，如图2。

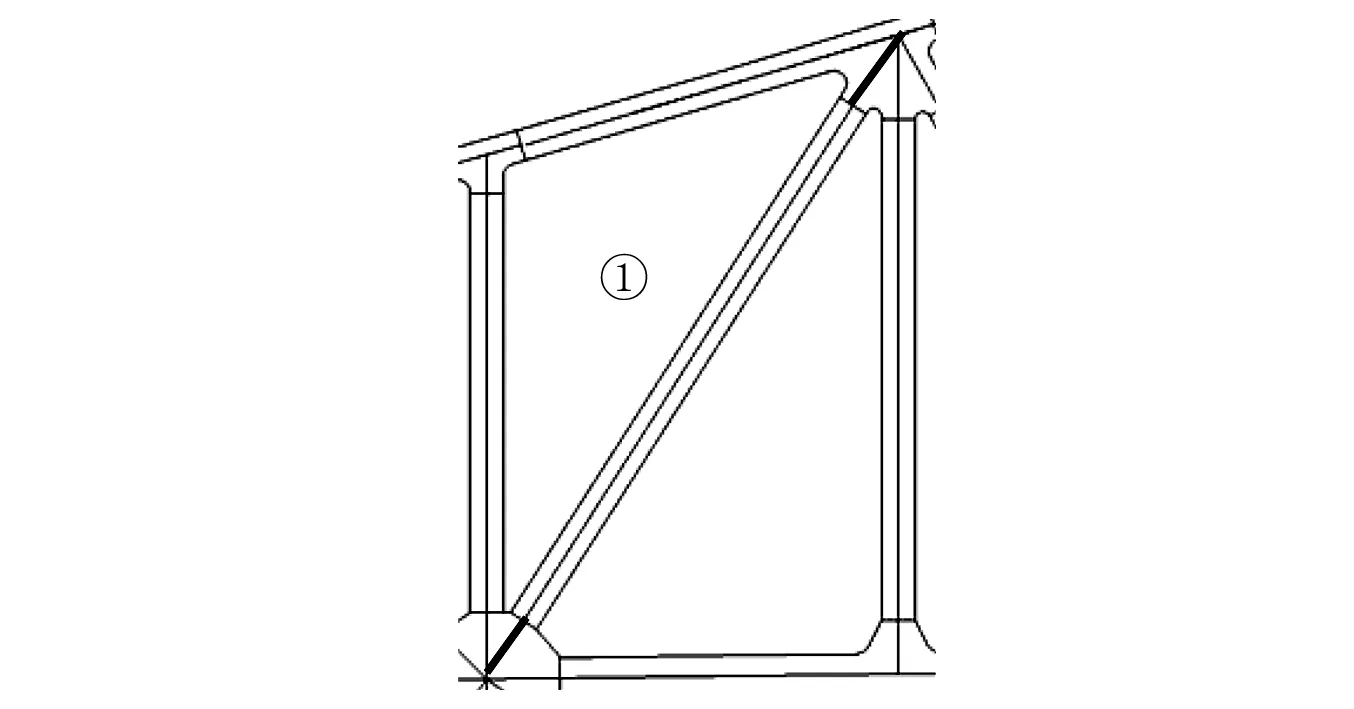
图2 节点板简化示意图Fig.2 Schematic diagram of simplified gusset plates

综上，对局部杆件的动力特性分析流程如图3所示

2.3 方法验证

谐响应分析是用于确定线性结构在承受随时间按正弦规律变化的荷载时的稳态响应，其目的是计算出结构在几种频率下的响应，并得到一些响应值(位移)对频率的曲线。从这些曲线峰值中，可以观察出峰值对应频率，即共振频率。谐响应分析常用于局部激励下，整体结构的响应问题。将局部杆件涡激振动时的涡脱力简化为均布正弦周期荷载进行加载，进行谐响应分析，曲线峰值处可认为是杆件涡振对应的弯曲基频[13]。以#1杆件为例，为得到杆件在横桥、顺桥两个方向的弯曲基频，基于有限元软件ANSYS，对杆件进行谐响应分析。对#1局部杆件每个单元节点上施加1 kN的正弦荷载，加载方向及工况如图4所示，并提取杆件中间节点的位移作为相应指标。计算频率区间为7～9.5 Hz，频率分割数100。分别使用上述“零密度”法与谐响应法进行动力分析，计算结果如图5与表2。

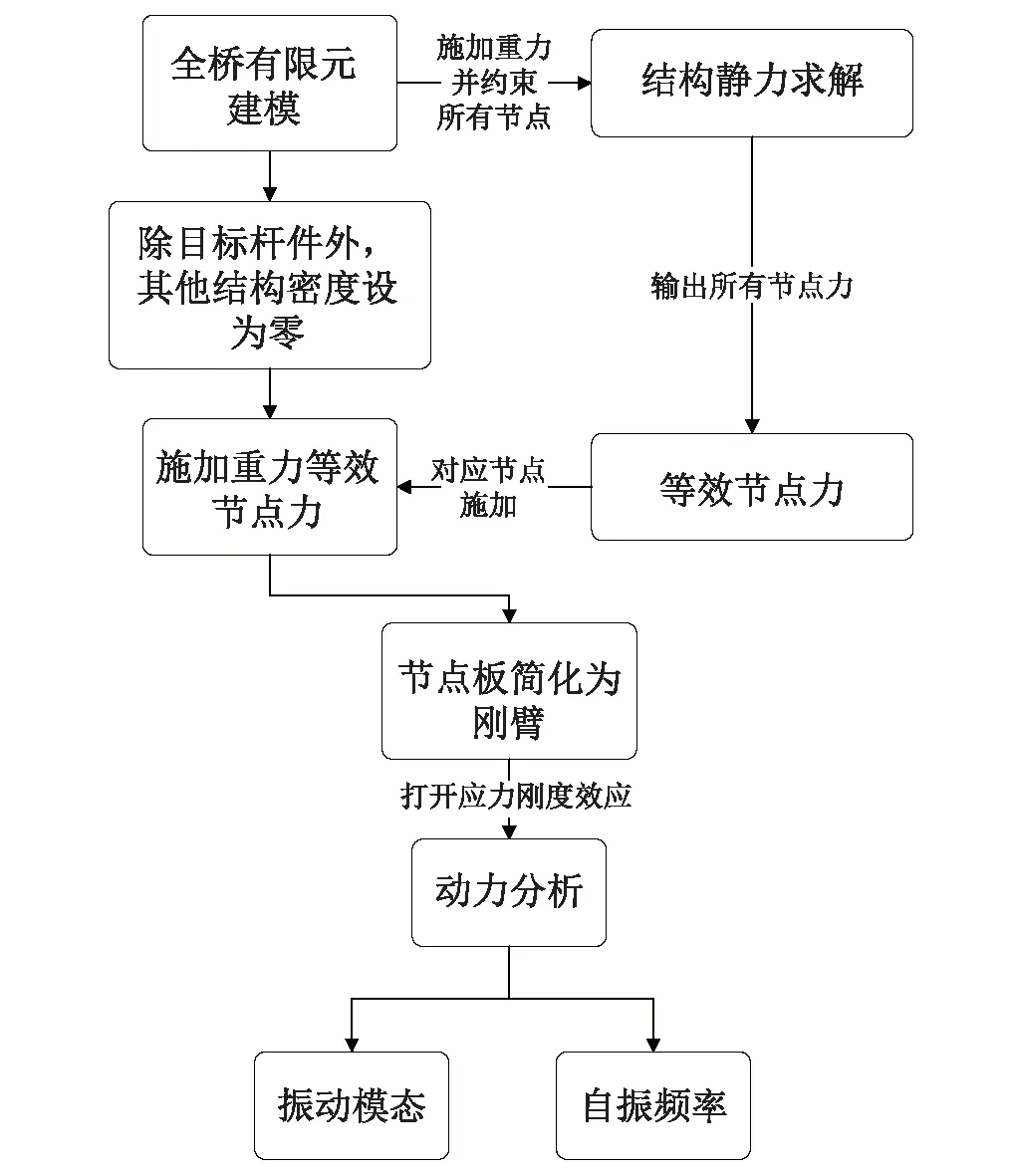
图3 局部杆件动力特性分析流程图Fig.3 Flow diagram to calculate the dynamic characteristics of local members

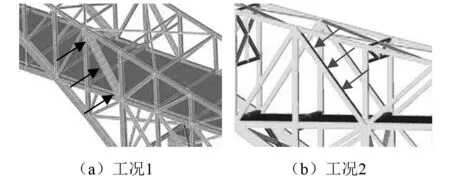
图4 谐响应分析加载工况示意图Fig.4 Schematic diagram of loading cases of harmonic response analysis

由图5、表2，谐响应分析结果显示，杆件横桥向位移峰值对应的频率，即横桥向弯曲基频为7.72 Hz，顺桥向位移峰值对应的频率，即顺桥向弯曲基频为8.79 Hz。“零密度”法计算结果与谐响应法很接近，基频计算误差在4%以下。值得注意的是，“零密度”法计算结果均比谐响应法大，这是由于其基本假设所决定的。“零密度”法将局部杆件动力特性求解问题，简化为了求解局部杆件在全桥其他杆件约束下的动力特性的问题。这种假设忽略了目标杆件之外，其他结构的质量贡献，从而使得自振频率的计算结果偏大。但由于当局部杆件振动时，其他结构的质量参与很小，因而对结果影响也有限。从计算时间上看，谐响应法计算时间是“零密度”法的36倍(计算机：Intel CoreTMi5@3.60 GHz)，且由于谐响应法是通过施加荷载来对频率进行估计，由于加载方式的限制，仅能对基频进行估计，而对于高阶振动频率，由于其振型复杂，谐响应法较难实现。同时，谐响应法查看频率对应振型较为不便，无法方便查看风致振动所需振型。而使用“零密度”法，可以在精度保证的情况下，较好解决上述问题。以下使用“零密度”法对#1、#2局部杆件进行分析。

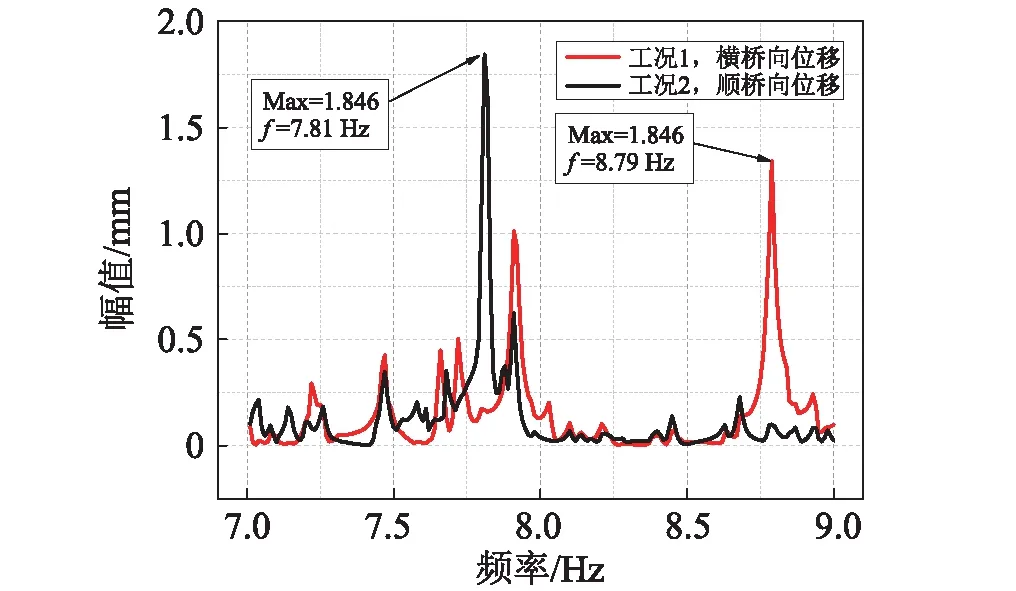
图5 谐响应分析计算结果Fig.5 Harmonic response analysis calculation results

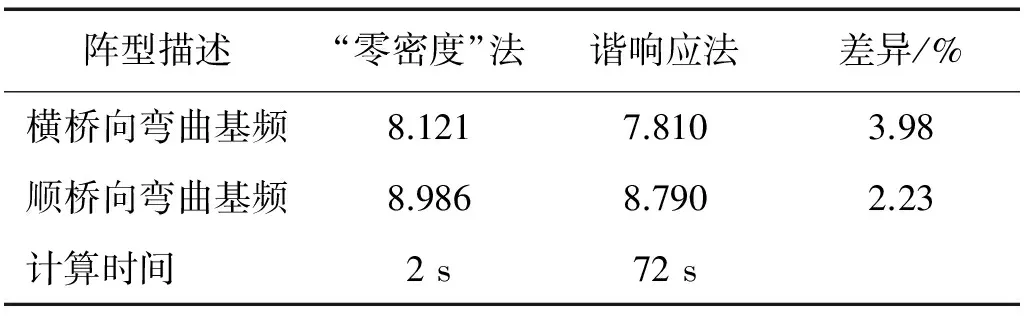
阵型描述“零密度”法谐响应法差异/%横桥向弯曲基频8．1217．8103．98顺桥向弯曲基频8．9868．7902．23计算时间 2s72s

3 局部杆件动力特性影响因素

3.1 约束条件影响

对#1杆件和#2杆件使用“零密度”法进行动力特性分析，各阶振型结果见图6、图7，并与采用杆端固结条件下的动力特性进行对比，见表3。

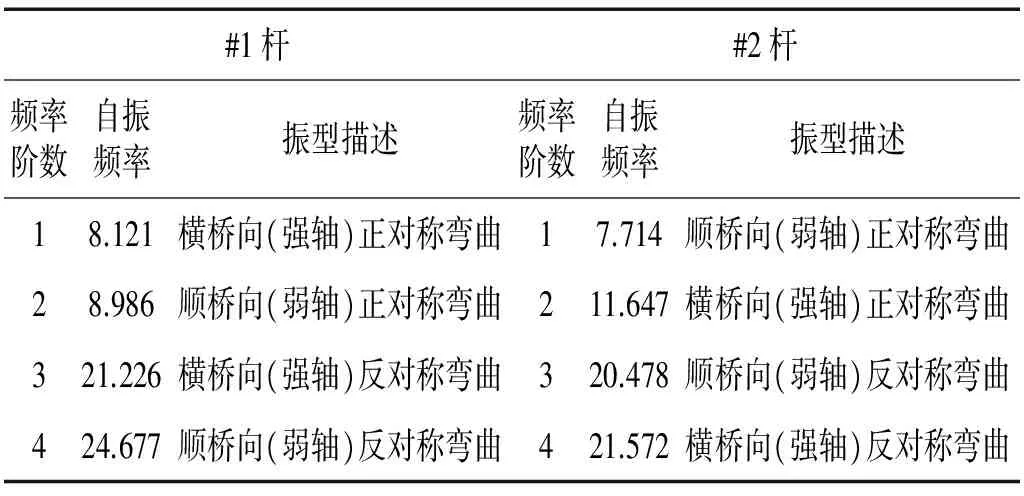
表3 #1和#2杆件动力特性

图6 #1杆件振型图(前4阶)Fig.6 Modal shape of #1 member (first 4 order)

图7 #2杆件振型图(前4阶)Fig.7 Modal shape of #2 member (first 4 order)

由图6、图7可见，使用“零密度”法进行动力特性计算，可以合理反映出目标杆件的振动情况。#1、#2杆件前4阶模态均为横桥或顺桥向弯曲。值得注意的是，从图6、图7的模态示意图可以看出，与杆端固结或铰接等对称约束不同，杆件的弯曲并非是严格的对称弯曲。这是由于在全桥状态下，杆件两端的约束不同造成的。以#1杆第一阶振型为例，由图6可见，杆件下端靠近拱脚处的约束由于桥面系及周围较强杆件的存在，其约束显然比上端拱圈附近更强，因此#1杆件整体呈现出靠上方杆端附近位移较大，靠下方杆端位移较小的特点。

为了对比使用“零密度”法与杆端固结边界下，杆件动力特性的差异，对#1、#2杆件杆端固结边界下的自振频率与模态进行了计算，计算及对比结果如表4、表5。其中，表4、表5中的自振频率按振型进行分类排序。

由表4、表5可见，使用“零密度”法考虑全桥约束时，与杆两端固结情况下相比，#1、#2杆件的自振频率与阶数产生了明显的差异。对于#1杆件，在全桥约束下，首先出现了强轴方向的弯曲振动，而在固结约束下，首先出现的是弱轴方向的弯曲振动，且前4阶各阶频率差异较大，均在35%以上。这是由于在全桥约束下，强轴方向(横桥向)的约束较弱产生的。大跨钢桁拱桥的设计是以受向下的荷载为主，竖向或顺桥向刚度很大，而横向刚度仅由拱片之间的横联提供，横联主要作用是保证左右拱片受力的整体性，本身强度较弱。对于#2杆件，在全桥约束下，弱轴向(顺桥向)自振频率与固结约束下自振频率差异较小，强轴向(横桥向)差异较大。这也是由于全桥结构在顺桥向刚度较大，对#2杆件而言接近固结约束，而全桥结构在横桥向刚度较小，与固结约束差异较大。值得注意的是，在全桥约束下，#2杆件一阶自振频率比两端固结下的一阶频率大2.65%。这是由于#2杆件是受拉杆件，在拉力作用下，杆件自振频率升高。可见，将杆端约束简单考虑为固结、铰接或使用某一约束系数计算局部杆件的动力特性是不准确的。

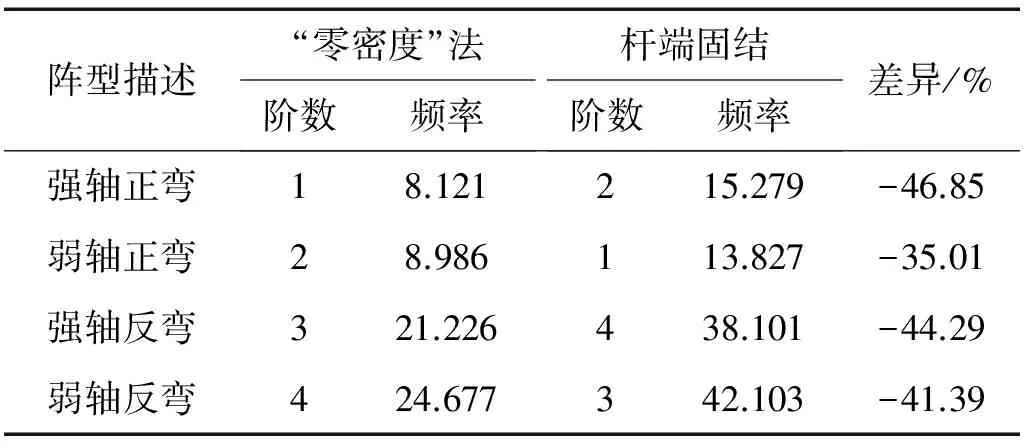
表4 #1杆件不同约束下动力特性对比

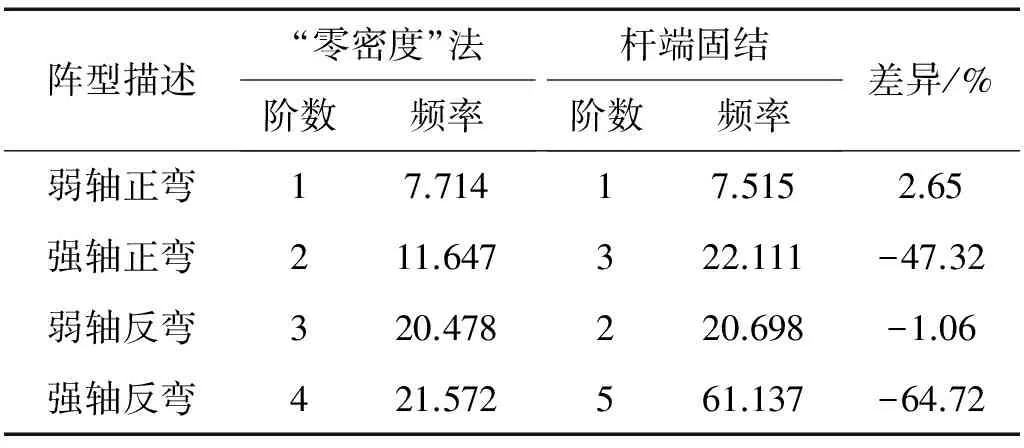
表5 #2杆件不同约束下动力特性对比

3.2 杆件内力影响

由于零密度法无法考虑重力，因此采用等效节点力的方式考虑重力对杆件自振频率的影响。对于局部杆件，等效节点力的影响机理是，一方面改变了全桥所有构件的内力，由于应力刚度效应，使全桥刚度发生变化，从而影响了目标杆件的约束条件；另一方面，由于等效节点力的施加，目标杆件中产生内力，而内力不同程度影响着杆件的自振频率。表6、表7分别#1杆件和#2杆件在有、无重力等效节点力作用下，杆件自振频率计算结果与对比。可以看出，对于#1杆件，杆件类型为压杆，加入重力等效节点力后，杆件产生内力，全桥刚度发生变化，各阶频率均有所降低。可见对于#1杆件，不考虑重力等效节点力时，计算的频率偏大，对抗风设计而言是偏危险的。对于#2杆件，杆件类型为拉杆，加入重力等效节点力后，1阶、3阶频率均有所升高，2阶、4阶频率基本不变。可见对于#1杆件，不考虑重力等效节点力时，计算的频率偏小，对抗风设计而言是偏保守的。

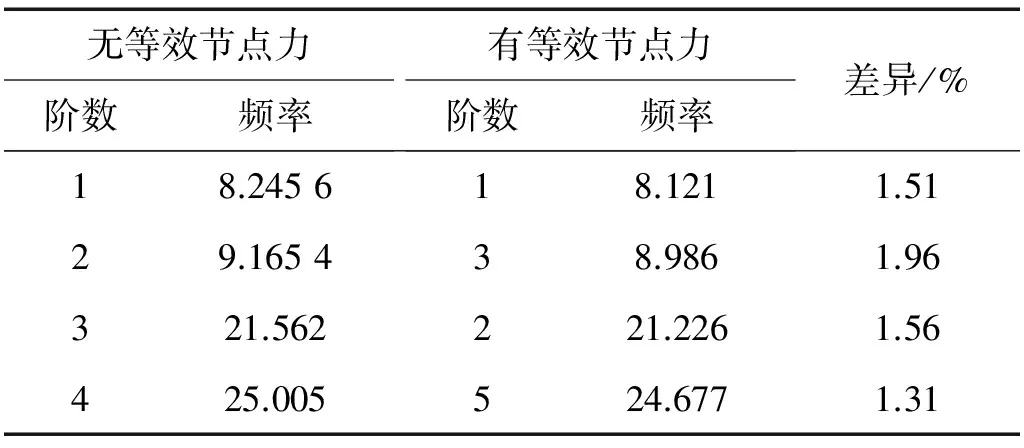
表6 #1杆件动力特性有无等效节点力对比

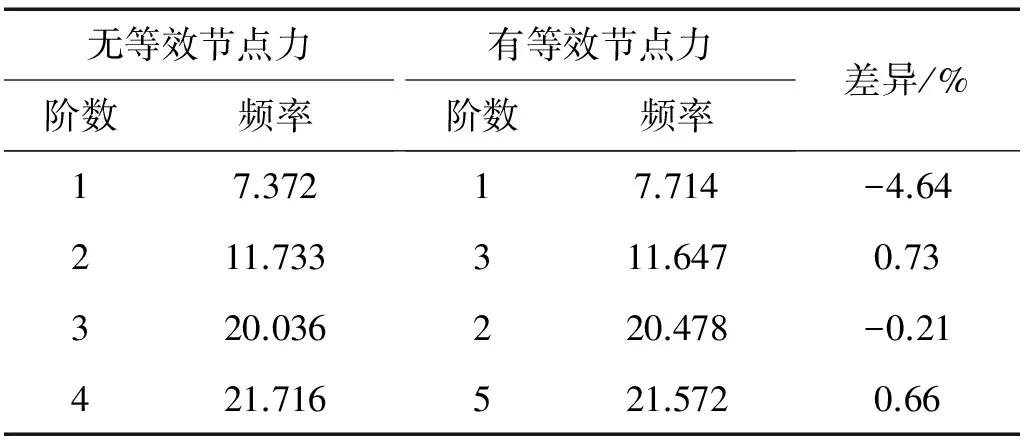
表7 #2杆件动力特性有无等效节点力对比

3.3 节点板长度影响

在框架结构或桁架桥梁有限元模型中，杆件与杆件之间直接以共节点的方式建模，忽略节点板的长度对整体结构的自振频率影响很小。但对于局部杆件，忽略节点板会显著增加杆件的长度，从而影响自振频率。表8、表9分别#1、#2杆件在不考虑与考虑节点板长度下，杆件自振频率的计算结果与对比。

由表8、表9可见，模型中节点板长度会显著影响杆件自振频率，最大差异达-37%以上。事实上，杆件的自振频率对杆件长度十分敏感，在模型中，若不考虑节点板长度，相当于增加了杆件长度，使自振频率显著减小。因此，对于局部杆件自振特性求解建模中，应全面考虑节点板的长度。

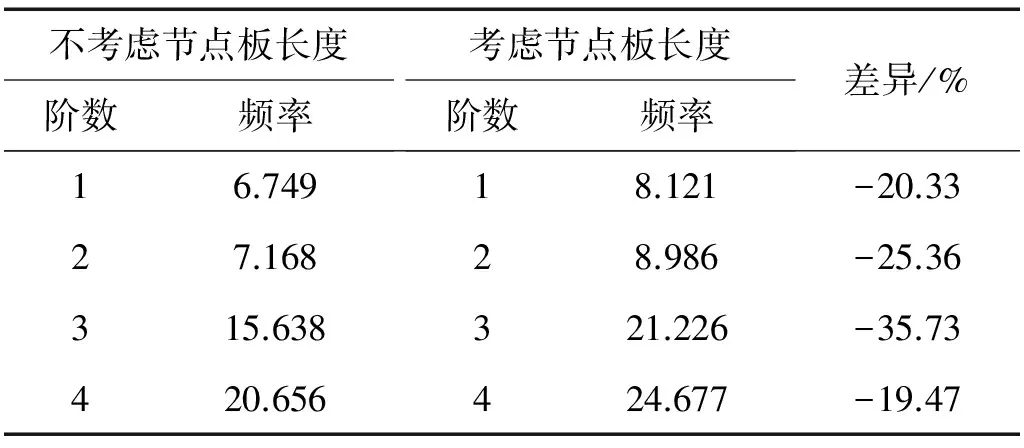
表8 #1杆件动力特性是否考虑节点板长度对比

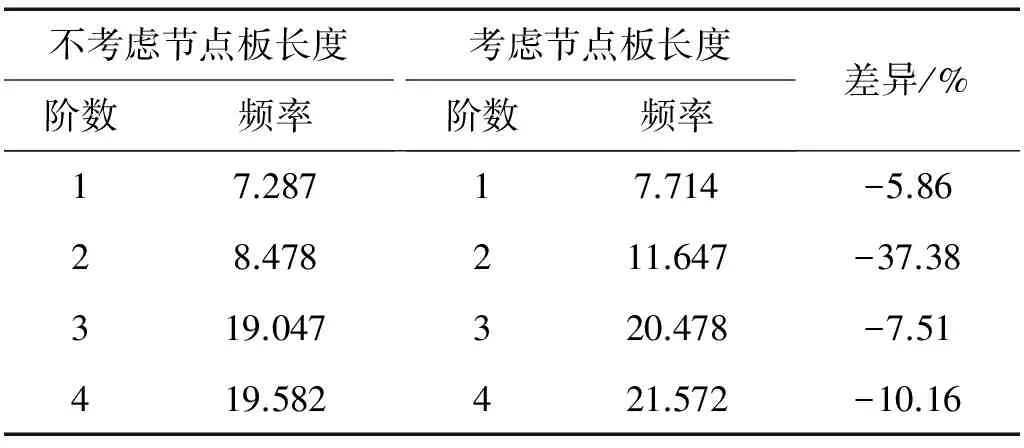
表9 #2杆件动力特性是否考虑节点板长度对比

4 杆件截面气动特性及涡振发生风速

涡激振动是大柔度构件在低风速下，在垂直于来流方向发生振动的物理现象，工程中应该避免发生涡激共振或将其振幅限制在可接受的范围内。研究假定局部杆件的涡激振动均发生在大致垂直于来流方向，即对应顺桥向的低阶振动模态。

旋涡脱落频率与来流风速及结构的截面形状有关，可用Strouhal数来描述[14]，如式(4)所示。

St=fD/U

(4)

式中：f为旋涡脱落频率；U为风速；D为物体垂直于来流方向平面上的特征尺寸。由CFD计算结果进行频谱分析，可求得截面涡脱频率f，由式(4)可求得截面Strouhal数St。

4.1 模型设置

计算区域设置如图8所示。计算模型尺寸为b示，断面中心位置坐标为(0，0)，其中L1=7b，L2=12b，B=11b，保证顺风向的阻塞率不大于5%。杆件截面采用无缩尺，以确保数值模拟的雷诺数与实际雷诺数相等。

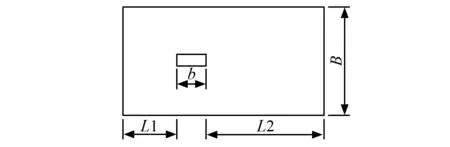
图8 计算域尺寸Fig.8 Size of the computational domain

采用长方形计算边界，迎风侧边界设置为速度进口条件(设置来流风速大小及方向条件)，背风侧边界选取为压力出口条件(静压大小设置与未扰动流场静压相同)进行模拟计算。上下边界条件视来流风速方向而定，若风向角为零，上下边界均设置为对称边界；若更改风向角，则下边界设置为速度进口，上边界设置为压力出口。

网格的划分对数值模拟计算结果有很大影响。为了能够满足计算结果的精确度并兼顾计算成本，网格划分采用放射性网格。对网格进行无关性检验，最终确定网格方案为边界层网格厚度0.001 m，网格总数约为10万左右，整体网格划分如图9所示，。

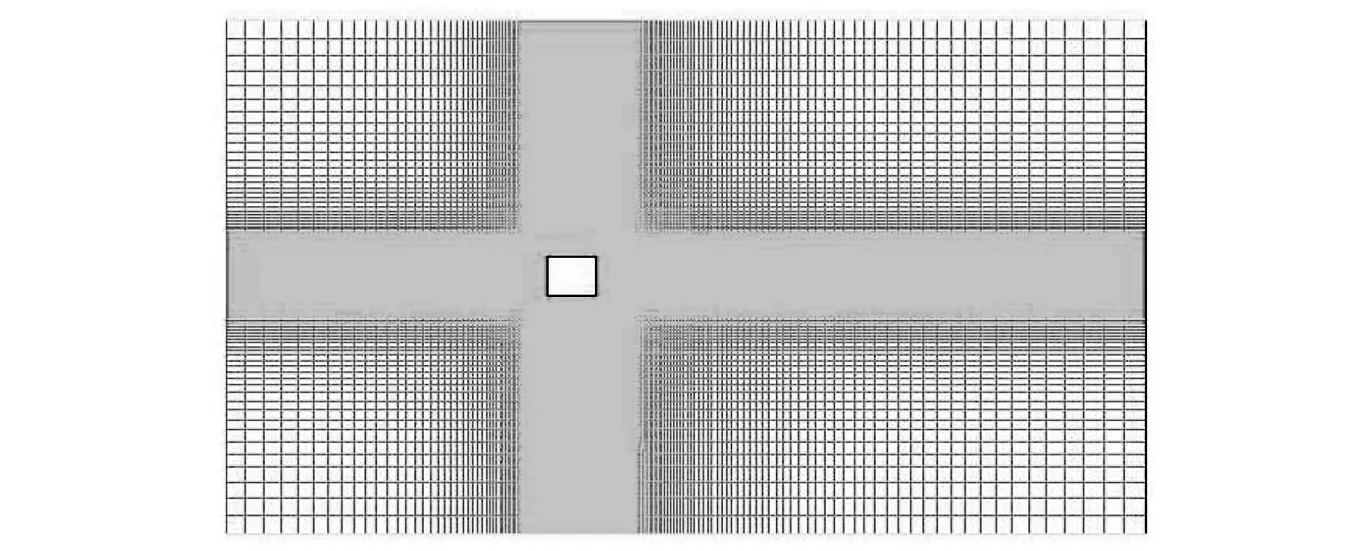
图9 计算域网格划分Fig.9 Mesh of the computational domain

使用大型商用软件FLUENT进行CFD计算。选用SSTk-ω湍流模型；用SIMPLE算法解决动量方程中速度分量和压力的耦合问题；动量方程、湍动能方程及湍流耗散率方程均采用二阶离散格式。湍流因子取0.5%，黏性系数取为2。采用非定常模型进行模拟，时间步长取5×10-4s。对#1、#2杆件截面在0°、10°、20°攻角下分别进行计算分析。钝体截面相对来说对雷诺数不敏感，加之涡振常发生在低风速下，故计算风速取30 m/s。

4.2 计算结果

对升力时程曲线进行频谱分析，得到卓越频率，即涡脱频率，根据式(4)求出截面在不同风攻角下的Strouhal数St，计算结果见表10。

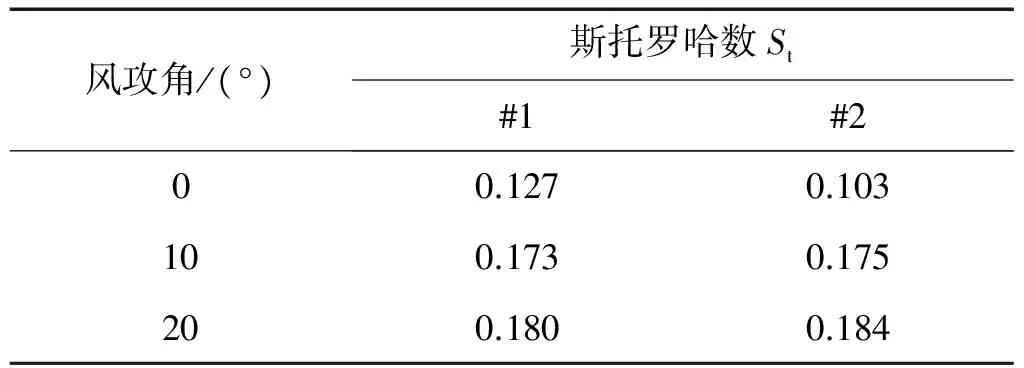
表10 杆件截面Strouhal数计算结果

4.3 涡振发生风速计算

杆件涡振发生风速可由式(5)计算

U=fD/St

(5)

式中：St为杆件截面斯托罗哈数；f为杆件自振频率，D为截面迎风面宽度；U为涡振发生风速。其中，自振频率f取杆件在垂直于来流风向(即顺桥向)的低阶弯曲振动模态，即，#1杆件取第二阶模态频率f#1=7.714 Hz，#2杆件取第一阶模态频率f#2=8.986 Hz。St采用表9计算结果进行取值。D按截面不同攻角下的迎风尺寸计算而得。涡振发生风速计算结果如表11所示。

由表11可见，两端固结边界条件下，计算结果与“零密度”法计算结果有明显差异。对#1杆件，使用两端固结边界条件时，过大地估计了杆端约束，且未考虑到杆件所受压力对频率的影响，从而高估了涡振发生风速，这在工程上可能是偏危险的。对于#2杆件，使用两端固结边界，未考虑杆件所受拉力对频率的影响，对涡振发生风速略有低估。

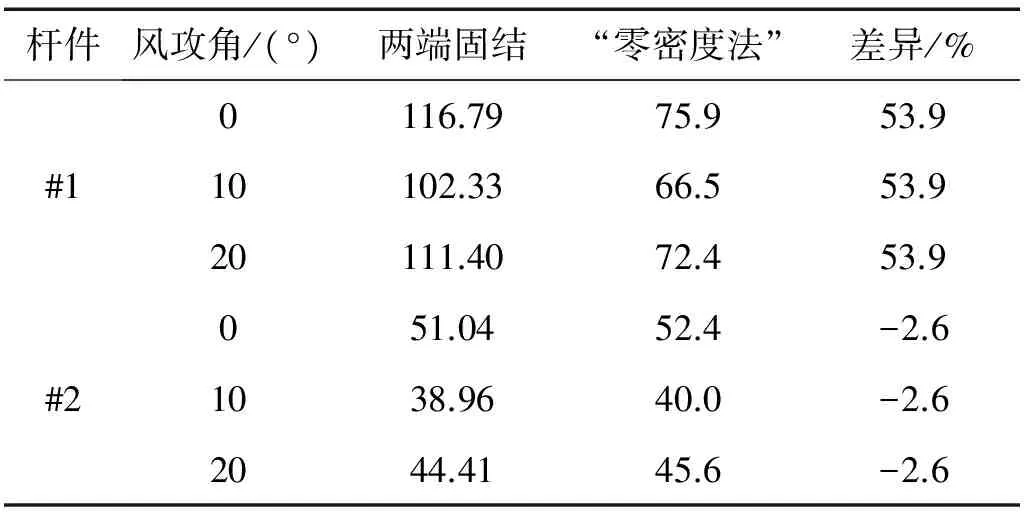
表11 涡振发生风速计算结果

总体来看，局部杆件涡振发生风速较高，其中#1杆件涡振发生风速在66 m/s以上，发生涡振可能性较低。#2杆件涡振发生风速在40 m/s左右，对于台风区内的沿海地区桥梁，这样的风速有可能引发杆件涡激共振。风攻角对杆件涡振发生风速有较大影响，#1、#2杆件均在10°攻角下发生风速最小，这与截面本身的气动特性有关。

5 结 论

(1)全桥约束下，局部杆件的边界条件复杂，难以直接确定，需对不同杆件具体进行全桥建模分析。“零密度”法分析结果表明，采用以往的固结边界条件可能会高估杆件(如#1杆件)的自振频率，差异可达46%以上。

(2)结构内力对局部杆件自振频率有不同程度的影响。一方面，内力通过影响全桥结构的刚度，改变了目标杆件的边界条件；另一方面，局部杆件内的拉力或压力会显著增加或减小杆件的自振频率。是否考虑结构内力对杆件自振频率影响可达5%左右。在局部杆件动力特性分析时，需考虑结构内力的影响。

(3)节点板长度会显著改变局部杆件的自振频率。虽然节点板对全桥动力特性分析影响很小，但对于局部杆件动力特性分析，由于杆件自振频率对长度较为敏感，节点板长度需进行合理考虑。节点板长度对自振频率的影响可达35%以上。

(4)总体来看，局部杆件涡振发生风速较高，其中#1杆件涡振发生风速在66 m/s以上，发生涡振可能性较小。#2杆件涡振发生风速在40 m/s左右，对于台风区内的沿海地区桥梁，这样的风速有引发杆件涡激共振的可能。风攻角对杆件涡振发生风速有较大影响，#1、#2杆件均在10°攻角下发生风速最小，这与截面本身的气动特性有关。

[ 1 ] 孙海涛.大跨度钢桁架拱桥关键问题研究[D].上海：同济大学,2007.

[ 2 ] 易伦雄. 南京大胜关长江大桥大跨度钢桁拱桥设计研究[J]. 桥梁建设,2009(5): 1-5.

YI Lunxiong. Design of Nanjing Dashengguan Yangtze river bridge large span steel truss arch bridge [J]. Journal of Bridge Construction, 2009(5): 1-5.

[ 3 ] 王福敏,徐伟. 重庆朝天门长江大桥主桥结构体系研究[J]. 公路交通技术,2005(增刊1): 23-28.

WANG Fumin, XU Wei. Study on structural system of main bridge of Chaotianmen Chongqing Yangtze river bridge[J]. Technology of Highway and Transport, 2005(Sup 1): 23-28.

[ 4 ] 李杏平,李爱群,王浩,等. 基于长期监测数据的苏通大桥桥址区风特性研究[J]. 振动与冲击,2010,29(10): 82-85.

LI Xingping, LI Aiqun, WANG Hao,et al. Study on wind characteristics of the bridge site of Su Tong Bridge Based on long-term monitoring data [J]. Journal of Vibration and Shock, 2010,29(10): 82-85.

[ 5 ] 欧阳克俭,陈政清,韩艳,等. 桥面中央开口悬索桥涡激共振与制涡试验研究[J]. 振动与冲击,2009,28(7): 199-202.

OUYANG Kejian,CHEN Zhengqing, HAN Yan, et al. The central opening suspension bridge vortex resonance and experimental study on the vortex [J]. Journal of Vibration and Shock, 2009,28(7): 199-202.

[ 6 ] RUDGE D, FEI C Y, RUDGE D, et al. Response of structural members to wind-induced vortex shedding[D]. Boston: Massachusetts Institute of Technology, 1991.

[ 7 ] 汪睿,吴刚,杨树耕. 导管架局部杆件固有频率计算实验研究[J]. 中国海洋平台,2012,27(4): 38-43.

WANG Rui, WU Gang, YANG Shugeng. Experimental study on the natural frequency calculation of the local bar of the jacket [J]. China Offshore Platform, 2012,27(4): 38-43.

[ 8 ] 张著名. 大跨度钢桁架拱桥局部杆件稳定问题研究[D].长沙：湖南大学,2007.

[ 9 ] 李晓猛. 岸边集装箱起重机圆截面杆件风致振动及控制的研究[D].上海：上海海事大学,2004.

[10] 邓洪洲,李峰,陈强,等. 输电塔典型节点钢管杆件动力特性研究[J]. 振动与冲击,2009,28(10): 60-63.

DENG Hongzhou, LI Feng, CHEN Qiang, et al. Study on dynamic characteristics of typical joints of the tube rod transmission tower[J]. Journal of Vibration and Shock, 2009,28(10): 60-63.

[11] 邓育林,彭天波,李建中,等. 大跨度三塔悬索桥动力特性及抗震性能研究[J]. 振动与冲击,2008,27(9): 105-110.

DENG Yulin, PENG Tianbo, LI Jianzhong, et al . Dynamic characteristics and seismic performance of the large span three tower suspension bridge[J]. Journal of Vibration and Shock, 2008,27(9):105-110.

[12] 张花. 大跨度钢—混组合桁架节点刚度研究[D].长沙：中南大学,2012.

[13] 詹昊,方秦汉,李万平. 钢桁拱桥吊杆涡激振动仿真分析[J]. 中国铁道科学,2009,30(2): 31-37.

ZHAN Hao, FANG Qinhan, LI Wanping. Simulation and analysis of vortex induced vibration of steel truss arch bridge [J]. China Railway Science, 2009,30(2): 31-37.

[14] 陈政清. 桥梁风工程[M]. 北京: 人民交通出版社,2005.