基于线扫描图像技术的立井多绳摩擦提升钢丝绳承载特性研究

蔡 翔， 曹国华， 韦 磊， 王 磊， 王海鑫(中国矿业大学 机电工程学院， 江苏 徐州 221116)

深立井提升中，一般采用多绳摩擦提升系统，为了保障其安全健康的运行，对其提升钢丝绳承载特性的研究极其重要。由于在承载运行的过程中，各提升钢丝绳受到摩擦轮绳槽磨损不同以及各钢丝绳捻制参数存在微小区别等影响，其张力很难保证一样，因此提升钢丝绳之间会存在张力差[1]。为了保证提升系统的安全可靠运行，《煤矿安全规程》第372条规定“多绳提升装置任一根提升钢丝绳的张力同平均张力之差不得超过±10%”[2]。

在提升运行过程中，提升钢丝绳的横向振动与其受力直接相关,为了掌握提升钢丝绳振动和张力特性，相关学者进行了论证、实验等研究。如朱艳军等[3]提出的基于CCD传感器的钢丝绳振动位移检测；梁敏等[4-5]应用Hamilton原理建立提升系统钢丝绳运动微分方程进行钢丝绳振动特性分析；王中琪等[6]利用提升绳张力研究钢丝绳在动负荷下的振动；王金峰等[7]采用水平位移法测提升钢丝绳张力和张力差等。由于建立振动微分方程[8-11]主要是在忽略外在次要因素的干扰下，从理论上进行分析，得出理想振动情况，而采用CCD传感器虽能够进行振动位移的检测，但数据分析量较大。针对上述分析，本文提出基于线扫描图像技术的多绳摩擦提升绳承载特性评估方法，实现同一时段内多根提升钢丝绳振动偏移量的实时检测和承载评估。首先通过线扫描技术结合VC++开发的图像采集程序来获取线单元图片，将数据传输给上位机，实现数据采集；其次采用基于小波变换的边缘提取算法，得出线单元图片中钢丝绳的中心位置相对于初始位置的偏移量；最后进行带通滤波及相应的FFT变换，消除外在噪声及其他因素的干扰，得到提升钢丝绳的时间位移图和幅频图，并掌握弦绳横向振动的固有频率，为提升钢丝绳张力的评估提供基础数据，同时也为立井多绳摩擦提升系统的健康运行提供保障。

1 线扫描检测模型

在多绳摩擦提升系统中，卷筒的转动会带动提升钢丝绳一起转动，从而实现矿井提升系统的提升和下放。在提升容器上下运行的过程中，提升钢丝绳起着悬吊提升容器并传递动力的作用，因此其安全性对整个提升系统至关重要。提升容器在上下运行过程中，弦绳会产生横向的振动，且其振动的频率与其张紧状态有关。为了能够方便检测提升钢丝绳的张力，掌握其运行过程中的承载特性，采用线扫描仪(SAPERA线阵相机)采集提升钢丝绳运行中的状态，其线扫描检测模型如图1所示，现场新郑煤电矿井提升钢丝绳振动检测和承载评估如图2所示。其中，电机带动卷筒正转时，上天轮上悬挂的箕斗处于空载下行的状态，下天轮上悬挂的箕斗处于满载上行的状态；当卷筒反转时，上天轮上悬挂的箕斗处于满载上行的状态，下天轮上悬挂的箕斗处于空载下行的状态。

1. 线扫描仪器；2. 滚筒；3. 弦绳；4. 主天轮；5. 副天轮；6. 主箕斗；7. 等重尾绳；8. 副箕斗

图1 线扫描提升绳模型

Fig.1 Line scan lifting rope model

通过现场实验，所获取的4根提升钢丝绳在某一时刻线单元图片如图3、图4所示。

图2 现场实验图

图3 1-2号提升钢丝绳的线单元图

Fig.3 Line unit diagram of No.1-2 hoisting rope

图4 3-4号提升钢丝绳的线单元图

Fig.4 Line unit diagram of No.3-4 hoisting rope

2 边界提取算法

线扫描图像技术获取的线单元图片经过VC++开发的程序实时处理，转化为灰度图数值后，需通过进一步的边界提取算法来识别提升钢丝绳的振动偏移量。设每获得一组线单元图片对应的数值矩阵为A1

A1=[a1,1a1,2…a1,2 047a1,2 048]

由于在灰度值图像中，颜色范围是0～255，考虑到线单元图片中会存在白色与灰色和灰色与黑色之间的过渡，数据之间的差距太小，因此在区分线单元图片中的提升钢丝绳所在位置时会存在较大的误差，所以需要将其数据范围放大。通过将原始数据转换为12位的二进制数据后，所得到的数值矩阵中的数值范围也变为0～4 095，且其中较大的数值偏白色，较小的数值偏黑色。则：

0≤ai,j≤4 095 (1≤i≤n,1≤j≤2 048)

ai,j表示线单元图片中的像素值，其中i表示线单元图片数，j表示线单元图片中像素的列数。

为了体现提升钢丝绳在整个运行过程中的承载特性，本实验获取了其完整运行的连续两个周期，且设置的获取线单元图片的帧率是100 f/s，因此线单元图片数较多，设在这两个完整的循环中获取的线单元图片数为n，则所有线单元图片组成的数值矩阵为A

(1)

进一步为了区分所获得线单元图片中的提升钢丝绳与背景，本文采用了基于小波变换的图像边缘提取算法[12]。根据式(1)，可知线单元图片中各像素值的位置坐标，因此以i，j对应所建XOY坐标系中的x和y值，则ai,j对应ax,y，通过边缘提取算法，以x，y为参数，建立边缘函数，得出边缘点的坐标值，从而确定提升钢丝绳边缘位置。

设二元函数h满足条件

则称h(x,y)为二元平滑函数，对于h(x,y)，定义两个小波函数

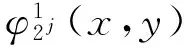
并记作

按照卷积和导数的关系，可以将其改写为

2j▽(f*h2j)(x,y)

(2)

定义在尺度时函数小波变换的模和幅角为

(3)

(4)

由式(2)～(4)可以看出，平滑后函数的突变点对应于梯度矢量方向A2jf(x,y)上M2jf(x,y)的局部极大值点，因此只需沿A2jf(x,y)方向检测M2jf(x,y)的局部极大值点，就可得到函数的突变点即图像的边缘点。对∀点(x0，y0)，若M2jf(x0,y0)再由A2jf(x0,y0)给定的梯度方向上取局部极大值，则称点(x0，y0)为f(x,y)的二进小波变换的模的局部极大值点。这些二进小波变换的模取极大值点的位置就给出了图像的一个多尺度边缘，从而实现图像边界的提取。

通过提取出边界后，可知边界以内为提升钢丝绳，边界以外为背景，则采用0，1矩阵置换法，将数值矩阵中所有对应提升钢丝绳的数值置换为1，所有对应背景的数值置换为0，此时数值矩阵A为只含0，1数值的矩阵。

像素列与实际尺寸之间的转换，每一张线单元图片中像素列都为2 048，其中钢丝绳所占像素列之和为

an,1+an,2+…+an,2 047+an,2 048=m

(5)

由于钢丝绳的实际直径为D，则转换的比率为η

η=D/m

(6)

通过小波算法的边界提取，可知每一张线单元图片中提升钢丝绳出现的边界点(x0，y0)，从而可得边界处首位像素列，即为kj(1≤j≤2 048)，则每一线单元中提升钢丝绳的中心位置为Pi(1≤i≤n)

Pi=kj+(m-1)/2

在线扫描检测提升钢丝绳时，提升钢丝绳的初始状态是静止的，则以第一张线单元中提升钢丝绳的中心位置为原点，而后面连续线单元相对于原点的像素列偏移量即为ΔPi

ΔP1=P1-P1=0

ΔPi=Pi-P1

(7)

由式(6)和(7)，可知实际的偏移量尺寸为S(mm)

S=η·ΔPi

3 试验结果及分析

3.1 提升参数

提升系统具体参数：提升高度为H=448 m，提升速度为v=10.89 m/s，箕斗自重为M0=28.5 t，额定载重M=20 t，提升钢丝绳直径D=44 mm、单位长度质量为ρ=8.08 kg/m，弦长l=47.5 m，采用等重尾绳。

当提升容器处于空载下行的匀速阶段时，在张力平衡装置调节下，可知每根提升钢丝绳在天轮端的张力T

(8)

根据弦绳振动固有频率的计算公式[13]

(9)

当i=1时，可得弦绳横向振动的一阶固有频率

f=1.202 Hz

3.2 结果及分析

通过式(9)可知提升钢丝绳张力与其多阶固有频率相关，且张力越大，其振动的固有频率越大。由于钢丝绳的承载特性直接由其张力反映，且多阶固有频率所对应的张力是一致的，因而分析其一阶固有频率便可掌握其承载特性，下面所述固有频率都为钢丝绳振动的一阶固有频率。为了掌握提升钢丝绳的承载特性，通过线扫描技术得到四根提升钢丝绳在提升过程中的实际振动偏移量随时间变化的曲线如图5所示。

(a) 1号钢丝绳实际振动位移图

(b) 2号钢丝绳实际振动位移图

(c) 3号钢丝绳实际振动位移图

(d) 4号钢丝绳实际振动位移图

为了明确的表明在提升钢丝绳承载的过程中，提升钢丝绳张力与提升绳振动固有频率之间的关系，本文通过选取提升容器上下运行1个周期来进行说明，在这个循环周期中，将其运行过程分为8个时间段，当主箕斗空载下行和满载上行时，t0段表示卸载箕斗静止时段，t1表示箕斗空载下行加速段，t2表示箕斗空载下行匀速段，t3表示箕斗空载下行减速段，t4表示箕斗装载静止时段，t5表示箕斗满载上行加速段，t6表示箕斗满载上行匀速段，t7表示箕斗满载上行减速段，且其中2号提升钢丝绳在不同时刻的振动情况，如图6所示。

图6 2号提升绳1个周期内的偏移图

由图6可知，t0与t4时段是装卸载过程，提升钢丝绳处于非工作状态，而t1与t3时段是加减速段，提升钢丝绳的张力处于变化状态，较难描述其与提升钢丝绳振动频率之间的联系，因此本文选择分析四根提升绳匀速段即t2时段的振动偏移情况如图7～13所示，同时为了能够分析不同时刻下的张力特性，将t2时段分为36～41 s，41～46 s，46～51 s，51～56 s四个时间段进行分析对比。由于通过理论分析知弦绳横向振动的频率为1.2 Hz左右，故将匀速段的振动偏移量进行0.5～2.0 Hz的带通滤波，减小外在因素的干扰，并将四个时间段滤波后的数据进行FFT变换，得到如图8～14所示的幅频图。

从以上分析的幅频图中，可以得出4根钢丝绳在匀速的各时间段内的的实际振动频率和张力值，如表1所示。

通过将匀速段分为四个时段进行分析，可知其幅频图几乎完全一致，由此可知在提升过程中，1～3号提升钢丝绳振动的固有频率为1.198 Hz，4号提升钢丝绳前期振动的固有频率为1.198 Hz，后期振动的固有频率为1.2 Hz，但与理论计算出的固有频率1.202 Hz极为接近。同时为了进一步验证本方法的合理性，分析了2号钢丝绳的二阶和三阶固有频率，分别为2.38 Hz和3.66 Hz，也与理论值2.404 Hz和3.606 Hz基本吻合，得到的钢丝绳张力与通过一阶固有频率得到的张力一致，因而评估钢丝绳承载特性时，可通过一阶固有频率来获得。通过表1可知1～4号钢丝绳的张力也几乎完全一致，在《煤矿安全规程》规定的范围内，表明该多绳摩擦系统的提升钢丝绳的受力比较平稳，其承载特性满足要求。

图7 1号钢丝绳匀速段的偏移图

Fig.7 Displacement diagram of No.1 hoisting rope in constant speed section

图8 1号钢丝绳匀速段的幅频图

Fig.8 Amplitude frequency diagram of No.1 hoisting rope in constant speed section

图9 2号钢丝绳匀速段的偏移图

Fig.9 Displacement diagram of No.2 hoisting rope in constant speed section

图10 2号钢丝绳匀速段的幅频图

Fig.10 Amplitude frequency diagram of No.2 hoisting rope in constant speed section

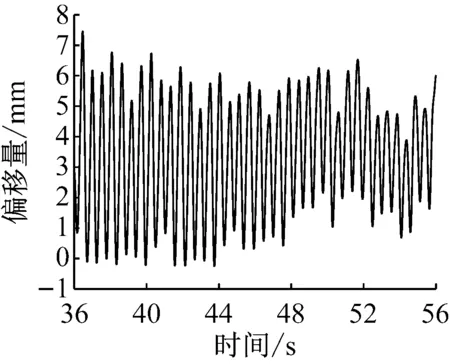
图11 3号钢丝绳匀速段的偏移图

Fig.11 Displacement diagram of No.3 hoisting rope in constant speed section

图12 3号钢丝绳匀速段的幅频图

Fig.12 Amplitude frequency diagram of No.3 hoisting rope inconstant speed section

图13 4号钢丝绳匀速段的偏移图

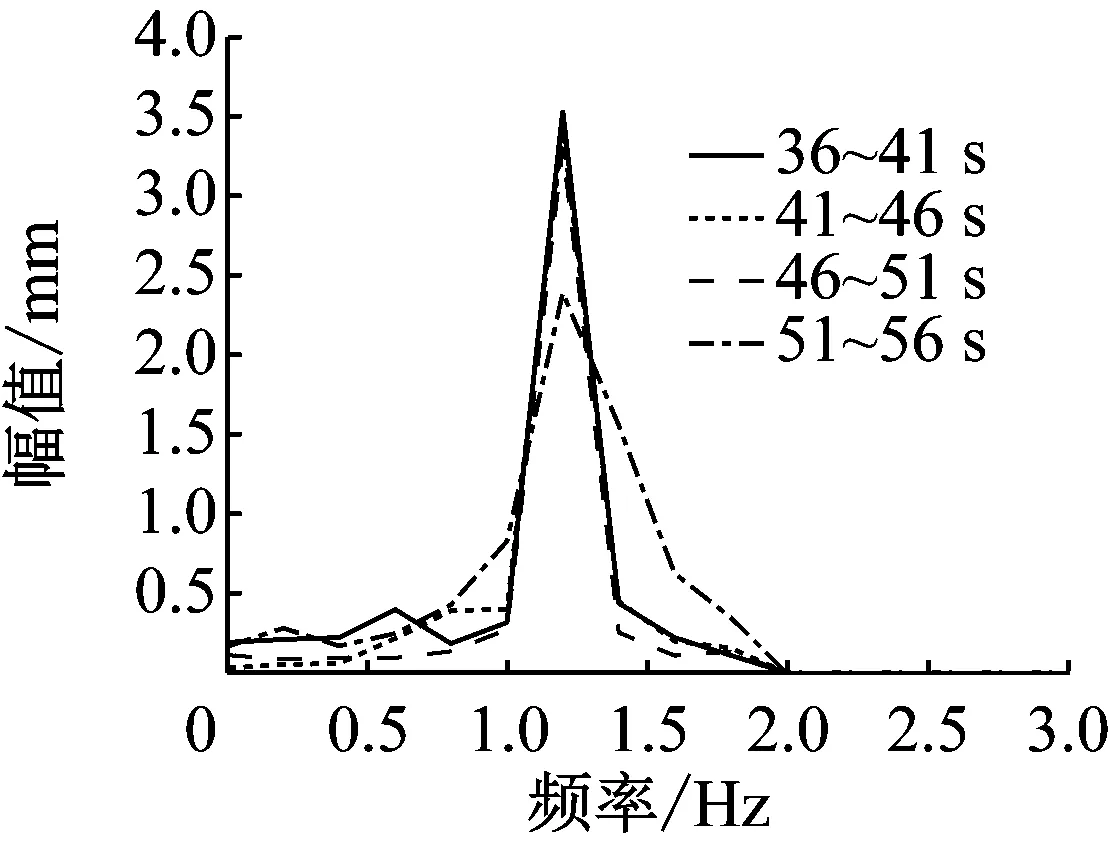
图14 4号钢丝绳匀速段的幅频图

时间/s1号钢丝绳2号钢丝绳3号钢丝绳4号钢丝绳频率/Hz张力/kN频率/Hz张力/kN频率/Hz张力/kN频率/Hz张力/kN36～411.198104.661.198104.661.198104.661.198104.6641～461.198104.661.198104.661.198104.661.198104.6646～511.198104.661.198104.661.198104.661.200105.0151～561.198104.661.198104.661.198104.661.200105.01

4 结 论

为了掌握立井多绳摩擦系统运行过程中提升钢丝绳的振动和受力情况，了解其承载特性，提出了安装测量便捷的基于线扫描图像技术的多绳摩擦提升钢丝绳承载特性检测方法。利用基于小波变换的图像边缘提取算法以及带通滤波和FFT变换，得到了弦绳振动的固有频率，并与理论计算结果对比验证了方法的有效性。评估了各提升钢丝绳的张力特性，掌握了各提升钢丝绳间的承载特性，为深井提升钢丝绳的健康状态检测提供了新的途径。

[1] 赵强，刘世春.提升钢丝绳张力差分析监测与调整[J].煤炭技术，2004,23(8):9-10.

ZHAO Qiang, LIU Shichun. Analyzing on monitoring and adjust of the steel rope tension difference of lifter[J]. Coal Technology, 2004,23(8):9-10.

[2] 煤炭工业部，煤炭安全规程[M].北京：煤炭工业出版社，2002：236-250.

[3] 朱艳军，肖兴明，甘立，等.基于CCD图像传感器的提升机钢丝绳振动位移检测[J].矿山机械，2013,41(3):64-66.

ZHU Yanjun, XIAO Xingming, GAN Li, et al. Detection on vibrative displacement of hoist wire rope based on CCD image sensor[J]. Mining & Processing Equipment，2013,41(3):64-66.

[4] 梁敏，寇子明.立井提升系统卡罐时钢丝绳的横向振动分析[J].煤炭技术，2015,34(1):289-291.

LIANG Min, KOU Ziming. Analysis of rope transverse vibration for block cage of mine hoisting system[J]. Coal Technology, 2015,34(1):289-291.

[5] 吴娟，寇子明，梁敏.摩擦提升系统钢丝绳横向动力学分析[J].振动与冲击，2016,35(2):184-188.

WU Juan, KOU Ziming, LIANG Min. Transverse dynamics analysis of rope in multi-rope friction hoisting system[J]. Journal of Vibration and Shock, 2016,35(2):184-188.

[6] 王中琪，李显寅.矿井提升钢丝绳在动负荷下的振动分析[J].矿山机械，2001(3):34-36.

WANG Zhongqi, LI Xianyan. Vibration analysis of mine hoisting rope under dynamic loading[J].Mining & Processing Equipment, 2001(3):34-36.

[7] 王金峰，蓝箭增，魏晓艳.多绳摩擦提升钢丝绳张力差的测定[J].矿山机械，2003,42(6):41.

WANG Jinfeng, LAN Jianzeng, WEI Xiaoyan. Determination of tension difference of multi rope friction hoisting rope[J]. Mining & Processing Equipment, 2003,42(6):41.

[8] 张长友，曹晓明，朱昌明.电梯钢丝绳的参数共振频带研究[J].振动与冲击，2007,26(10):165-167.

ZHANG Changyou, CAO Xiaoming, ZHU Changming. Study on parametric resonance frequency band of elevator ropes[J]. Journal of Vibration and Shock, 2007,26(10):165-167.

[9] 王则，赵子龙，杨晓辉.提升钢丝绳的纵向振动特性研究[J].太原科技大学学报，2015,36(3):241-244.

WANG Ze, ZHAO Zilong, YANG Xiaohui. Study on longitudinal vibration characteristics of hoisting rope[J]. Journal of Taiyuan University of Science and Technology, 2015,36(3):241-244.

[10] 寇保福，刘邱祖，刘春洋，等.矿井柔性提升系统运行过程中钢丝绳横向振动的特性研究[J].煤炭学报，2015,40(5):1194-1198.

KOU Baofu, LIU Qiuzu, LIU Chunyang,et al. Characteristic research on the transverse vibrations of wire rope during the operation of mine flexible hoisting system[J].Journal of China Coal Society, 2015,50(5):1194-1198.

[11] 曹国华，朱真才，彭维红，等.箕斗在装载过程中的振动特性研究[J].煤炭学报，2007,32(3):327-330.

CAO Guohua, ZHU Zhencai, PENG Weihong,et al. Study on vibrant characteristic in skip’s loading[J]. Journal of China Coal Society, 2007,32(3):327-330.

[12] 高国荣，刘冉，羿旭明.一种改进的基于小波变换的图像边缘提取算法[J].武汉大学学报，2005,51(5): 615-619.

GAO Guorong, LIU Ran, YI Xuming. A revised image edge detection method based on wavelet[J]. Journal of Wuhan University, 2005,51(5):615-619.

[13] 杨揆一.提升过程中钢绳的横向振动[J].矿山机械，1981，43(11):10-16.

YANG Kuiyi. Transverse vibration of steel rope in hoisting process[J]. Mining & Processing Equipment,1981,43(11):10-16.