误差理论在杨氏模量实验数据处理中的应用
2018-03-27张军朋
郑 颖 张军朋
(华南师范大学物理与电信工程学院 广东 广州 510006)
物理学是一门以实验为基础的自然科学.学生通过实验测量,会得到与实验相关的数据.而科学的数据处理和分析是大学物理实验中一个至关重要的环节.对同一组实验数据引入不同的处理方法不仅可以起到让学生掌握多种数据处理方法的作用,而且能够使学生对所学的误差基本理论知识有更加深入的理解.在教学中,教师可以结合具体的实验,引导学生采用多种方法来进行实验数据处理.本文以拉伸法测定金属丝的杨氏弹性模量为例,基于误差理论,用合成不确定度和扩展不确定度两种方式来表示金属丝直径的测量结果,并以统计的方法对金属丝直径测量过程中是否存在随机误差、系统误差以及粗大误差进行鉴别;同时,采用逐差法和用最小二乘法进行线性回归两种方法求解杨氏模量,以期给大学物理实验的教学以及学生在处理实验数据时提供一定的参考.
1 拉伸法测定金属丝的杨氏弹性模量
1.1 实验原理
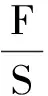
(1)
比例系数Y是该材料的杨氏弹性模量,简称为杨氏模量,它在数值上等于产生单位应变的应力.在SI制中杨氏弹性模量Y的单位为N/m2.杨氏模量是描述金属材料抗弹性形变能力的物理量,它与物体所受外力的大小和物体的形状无关,只决定于材料的性质.
实验中,在外力F的拉伸下,金属丝的伸长量ΔL是一个微小变量,一般难以测量.本实验采用的是光杆杠法来测量金属丝微小长度的变化.
如图1所示,金属丝为原长时,与望远镜中叉丝横线重合的标尺读数为x0,当金属丝伸长ΔL时,光杠杆后足就随之移动ΔL,镜面也要绕前足连线转动一个微小角度φ,与望远镜叉丝横线重合的标尺读数x0相应地变为x1.由光的反射定律可知,∠x1Ox0=2φ.设光杠杆的后足到两前足连线的垂直距离为K,镜面到标尺的垂直距离为D,x1与x0的距离为Δx
Δx=|x1-x0|
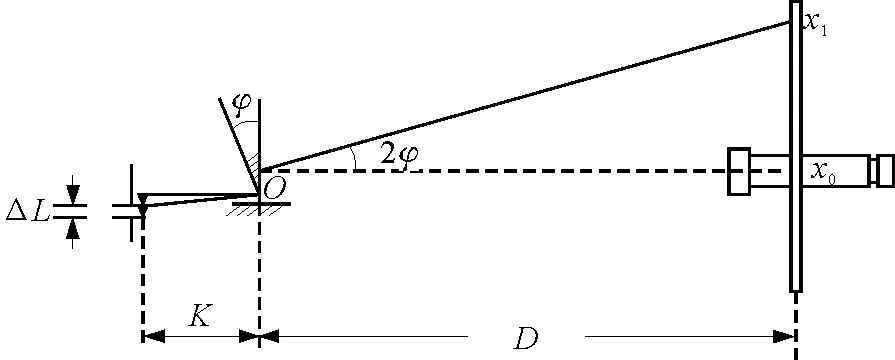
图1 光杆杠测量原理图
在金属丝长度变化ΔL很小的情况下
有
(2)
由式(2)可知,金属丝长度的微小变化量ΔL,经光杠杆转变为角度的微小变化量φ,再经过望远镜和标尺把它转变为较大的标尺读数变化量Δx.其作用就像杠杆一样起到放大的作用,所以称为光杠杆法[1].
比值
就是光杠杆法的放大倍数.将式(2)代入式(1),得
(3)
设金属丝直径为d,则其截面积
又
F=mg
代入式(3)后整理得
(4)
1.2 数据记录表
实验数据如表1和表2所示.
表1加砝码和减砝码时标尺的读数
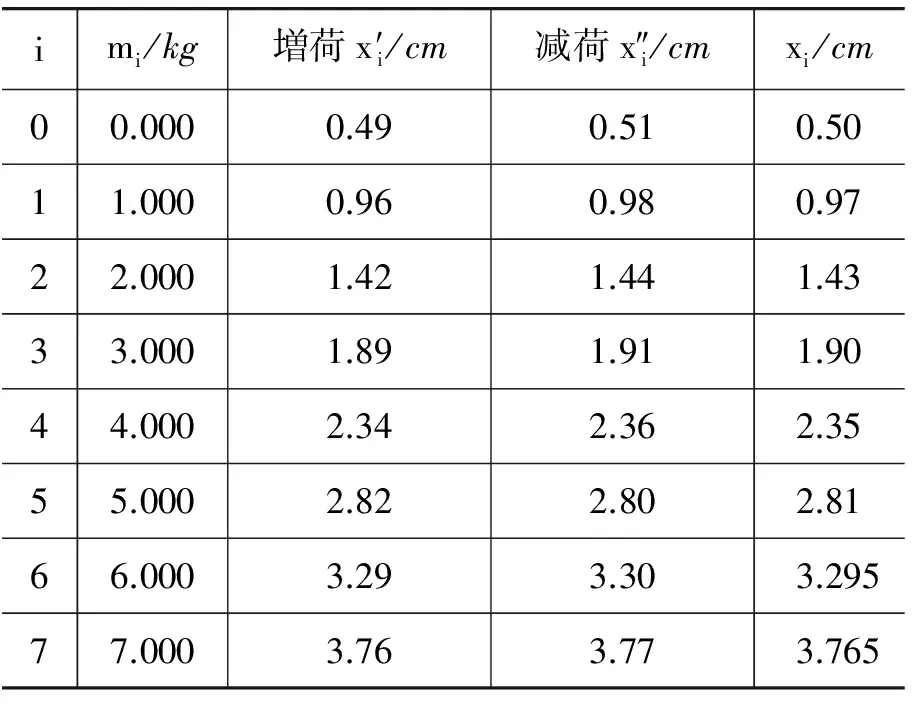
imi/kg増荷x′i/cm减荷x″i/cmxi/cm00.0000.490.510.5011.0000.960.980.9722.0001.421.441.4333.0001.891.911.9044.0002.342.362.3555.0002.822.802.8166.0003.293.303.29577.0003.763.773.765


表2 金属丝的直径和其他长度测量结果
2 金属丝直径测量的实验数据处理
2.1 测量值的误差判断
为获得尽可能精确的结果,实验时往往要根据误差的性质来选择数据处理方法以及误差计算与评定方法等.根据误差的性质,误差可分为随机误差、系统误差和粗大误差.误差是不确定度的基础,计算不确定度首先要研究误差的性质、规律,才能够更好地估计不确定度分量.因此,测量的实践要求对不同性质的测量误差做出确切的区分.
2.1.1 正态性检验
正态分布统计检验常用的检验方法有夏皮罗-威尔克检验、偏态系数检验、峰态系数检验.这里我们使用夏皮罗-威尔克检验,又称为W检验[2].该检验对样本容量虽没有要求,但主要适用于小样本,3≤n≤50时检验效果最佳,并且计算简便.
假设金属丝直径测量的10个数据均服从统一概率分布,且检验数据符合正态性分布,具体步骤如下:
(1)将样本的观测值由小到大排列成为
d1=0.587≤d2=0.588≤……≤d10=0.592
(2)计算检验统计量
式中,a(i,n)由夏皮罗-威尔克系数表查出,分别为
a(1,10)=0.573 9a(2,10)=0.329 1
a(3,10)=0.214 1a(4,10)=0.122 4
a(5,10)=0.039 9
计算得到W=0.943.
(3)查表.给定显著性水平α=0.01,查出夏皮罗-威尔克值W(10,0.01)=0.784.
(4)判断.因为W=0.943>W(10,0.01)=0.784,故接受正态性检验.
2.1.2 判断系统误差
按随机误差的统计规律做出某种统计法则,看测量数据系列是否与之相符,若不相符合则说明该测量数列包含系统误差.这类方法很多(包括残差校核法、阿贝-赫梅特判别法、残差总和判别法、标准差比较法、数据比较法等),适应性各有差异.由于较少涉及测量本身具体内容,仅针对测量数据即可做出判断,因而便于掌握和使用.
根据判断方法的适应性,采用残差校核法和标准差比较法[3]进行判断.
(1)残差校核法
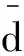
(2)标准差比较法
按贝塞尔公式计算
得
s1=0.001 713
按彼得斯公式计算
得
s2=0.001 849
则
所以测量列中不存在系统误差.
2.1.3 判断粗大误差
判断粗大误差时,首先要准确找出可疑测量值.一般测量列中,残余误差绝对值最大者即为可疑值.它是测量列中最大测得值或最小测得值之一.其次,可根据测量准确度要求和测量次数选择判别准则(包括拉伊达准则、格拉布斯准则、狄克逊准则、肖维勒准则等).
因为测量次数为10,在3≤n<25这个范围内,故用格拉布斯准则[4](取显著性水平α=0.01)来判别可疑数据.
(1)将测量值从小到大排序,找到最小值
d(1)=0.587
最大值
d(10)=0.592
(2)由上面的结果可知该测量数据服从正太分布且
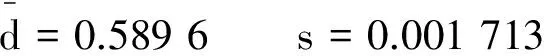
(3)计算
故先怀疑G(1)是否含有粗大误差.
(4)取显著性水平α=0.01,查表得临界值G(0)(10,0.01)=2.41.
(5)判断,因为G(1) 测量结果可以分为合成标准不确定度表示方式和扩展不确定度表示方式[5]. 2.2.1 合成标准不确定度表示方式 d的算术平均值 任何一次测量值的标准偏差 测量值d的不确定度A类分量 uA=σd=0.001 713 mm 因为螺旋测微计的Δ仪=0.004 mm,所以B类分量 不确定度 测量结果 d=(0.590±0.003) mm 2.2.2 扩展不确定度表示方式 算术平均值的标准差 ±3.25×0.000 541 698 2 mm= 0.001 8 mm≈0.002 mm 最后测量结果 (p=0.99) 当自变量为等间距变化,且两物理量之间又呈线性关系时,为充分利用实验测量中采集的数据,达到对数据取平均(即保持多次测量的优越性,减少偶然误差) 的效果,通常采用逐差法来处理实验数据[6]. 代入数据得 代入数据得 钢丝杨氏弹性模量的平均值 代入数据得 钢丝的杨氏弹性模量标准值 Y′=2.00×1011N/m2 百分差 估算杨氏模量的不确定度 代入数据得 测量结果 Y=(2.06±0.02)×1011N/m2 最小二乘法是一种数学原理,它在误差的数据处理中作为一种数据处理手段.用此原理可以获得最可信赖的测量结果,使各测量值残余误差的平方和为最小[7].而回归分析作为最小二乘法的一个应用特例,是处理变量间函数或相关关系的一种数理统计方法,其基本思想也是应用数学的方法,对大量的观测数据进行处理,从而得出比较符合事物内部规律的数学表达式[8]. 3.2.1 外加张力与金属丝长度变化关系的线性回归方程 相关数据如表3所示. 表3 回归系数计算表[8] 续表3 ∑7i=0mi=28kgm-=3.5kg∑7i=0xi=17.02cmx-=2.13cmlmm=∑7i=0(mi-m-)2=42kg2 lxx=∑7i=0(xi-x-)2=9.0867cm2lmx=∑7i=0(mi-m-)(xi-x-)=19.535kg·cm 计算线性回归系数b和回归常数b0: 故得回归方程数学表达式 x=0.503+0.465m 3.2.2 回归方程的方差分析和显著性检验 回归方程的方差分析表如表4所示. 表4 方差分析表[8] 查F分布表,得F0.01(1,8)=11.26 3.2.3 求解杨氏模量 由杨氏模量公式得 对于拉伸法测定金属丝的杨氏弹性模量实验,除了传统的用合成标准不确定度和逐差法的实验数据处理方法外,本文也运用误差的性质、扩展不确定度、最小二乘法和线性回归等理论进行误差分析和数据处理,提出了新的数据处理思路,让学生更好地理解误差理论与数据处理的基本概念和基本方法.从教学角度讲,教师在掌握了各种实验数据处理方法特点的基础上,可以通过具体实验的教学,在实验数据处理中培养学生仔细认真、一丝不苟的科学态度. 1 张昌莘,王德明,方运良.三级物理实验教程.北京:化学工业出版社,2010 2 马宏,王金波.仪器精度理论.北京:北京航空航天大学出版社,2009 3 丁振良.误差理论与数据处理.哈尔滨:哈尔滨工业大学出版社,2002 4 熊艳艳,吴先球.粗大误差四种判别准则的比较和应用.大学物理实验,2010(1):66~68 5 沙定国.误差分析与测量不确定度评定.北京:中国计量出版社,2003 6 向泽英,罗浩,邓先金,等.以Excel逐差法为例实现初学者数据处理方式的转变.大学物理实验,2016(1):108~111 7 方彦军,程继红.检测技术与系统.北京:中国电力出版社,2006 8 钱政,贾果欣.误差理论与数据处理.北京:科学出版社,20132.2 金属丝直径测量结果的表示
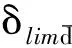
3 杨氏模量的求解
3.1 逐差法
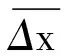
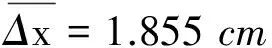
3.2 用最小二乘法进行线性回归
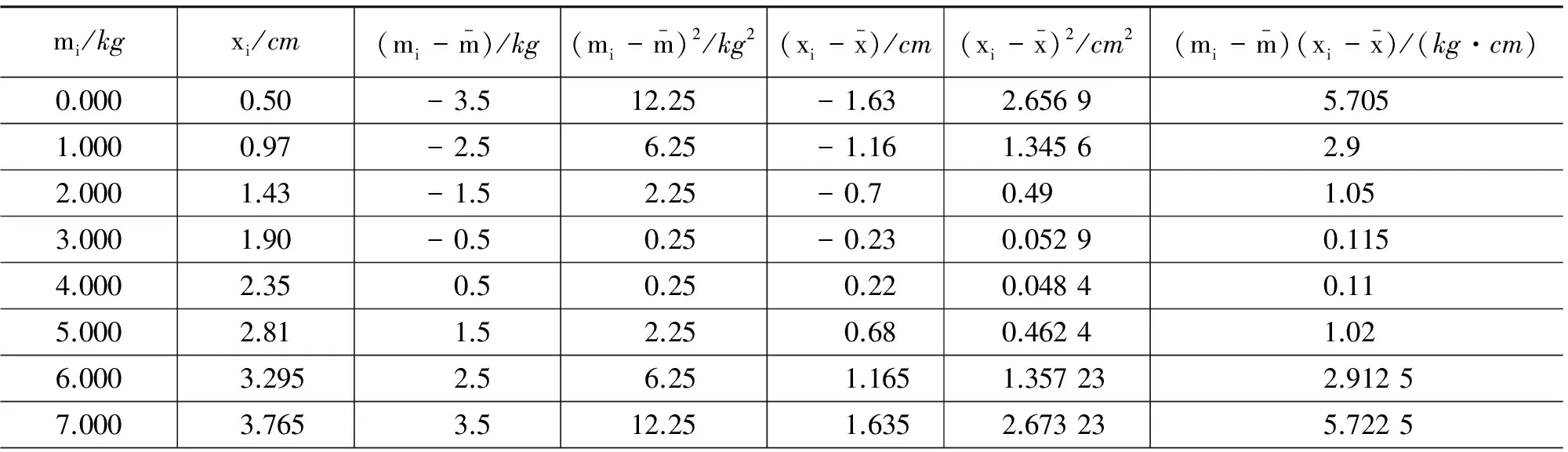
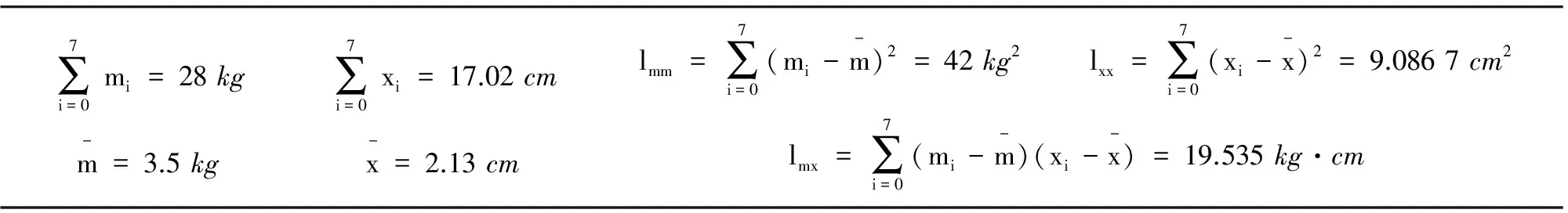
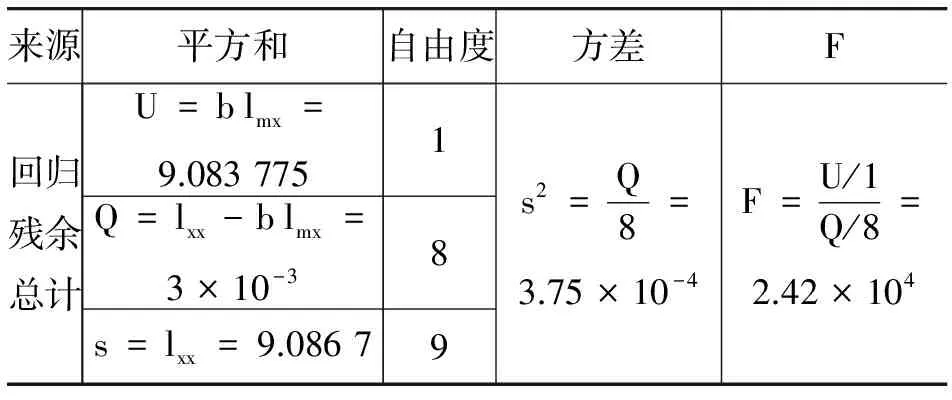
4 结论
