关于牵连体速度及加速度变化规律的分析
2018-03-27许龙
许 龙
(安徽省太和一中 安徽 阜阳 236600)
杨培军
(阜阳市教育局物理教研室 安徽 阜阳 236000)
在备战高考的复习中,常遇到绳牵连体问题,许多学生对此非常棘手;尤其是寻找牵连体速度极值位置时经常出现这样的错误:两者同时达到速度极值,速度极值位置在二者静止的位置.其实不然,利用牛顿第二定律、能量守恒和一定的数学知识推导后就会发现两牵连体速度并非同步变化.下面笔者就结合一道高考模拟题来分析牵连体速度极值的位置.
解决此类问题时要明确两点:牵连体沿着绳方向速度大小相等,能量守恒.
1 真题回放
【题目】(2017年南通高三第一次调研)如图1所示,足够长的光滑直杆倾斜固定,杆上套有质量为m的小滑块A,用足够长、不可伸长的轻绳将A与另一质量为2m的小物块B绕过光滑的定滑轮相连接,A位于O点,此时滑轮左侧轻绳恰好水平.现将A从O点由静止释放,B在运动过程中不触碰滑轮和直杆,则( )
A.滑块A释放瞬间,绳对A的拉力为2mg
B.滑块A速度最大时,物块B的速度也最大
C.滑轮左侧的轻绳与直杆垂直时,滑块A速度最大
D.滑轮左侧的轻绳与直杆垂直时,滑块A机械能最大
解析:设初始时杆与水平面夹角为α,滑块A释放瞬间绳子拉力为T,对A,B受力分析可得
(1)
由几何关系得aAcosα=aB,整合后有
故A选项错误.
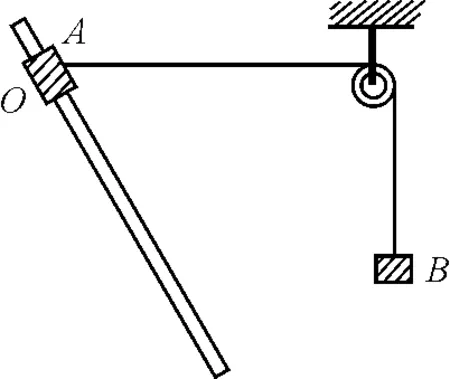
图1 题图
A下滑至滑轮左侧的轻绳与直杆垂直的过程中,A和B的高度皆降低,速度均增大;此后A继续下滑,假设A稍下滑一点,绳与杆垂直方向夹角为β(β极小),绳子拉力为F,对A和B受力分析得
(2)
由几何关系可得
aAsinβ=-aB
联立后有
故A的速度将继续增大,B的速度将减小,由此可知选项B,C错误.
A下滑至绳与杆垂直的过程中,绳子拉力对A做正功,机械能增加;滑过与杆垂直位置后,绳子拉力对A做负功,A机械能减小,故D选项正确.
答案解析并无错误,但并未对两牵连体速度和加速度进行详细推导,其变化规律到底如何并未作详细说明.下面笔者就这种牵连体的一般模型进行分析计算,寻找速度和加速度表达式,并利用特殊值验证计算.
2 速度变化规律
设光滑杆与水平夹角为α,经过一段时间绳与水平夹角为θ,滑轮左侧绳长为L,A的速度v1,沿杆运动位移x;B的速度为v2,亦为A沿绳子上的分速度,此时二者速度关联v2=v1cosα+θ,如图2所示.由此可知,当
时,A沿绳子方向分速度沿绳向上,B向下运动,当
时,A沿绳子方向分速度沿绳向下,B向上运动;所以当
时,A,B重力做正功,B速度为零,A机械能最大.
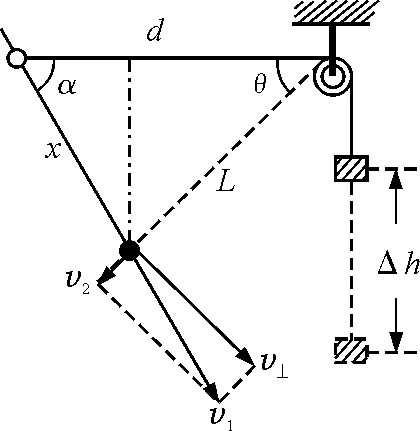
图2 两物速度与位置图像
在滑块A运动的任意位置、初点、绳子与滑轮悬点围成的三角形,内角分别为α,θ,π-α+θ,可由三角形正弦定理得
(3)
可得A下滑位移x和B沿绳向下位移Δh


(4)
同时利用机械能守恒得到其速度大小
(5)

(6)
2sinα+θ-2sinα·
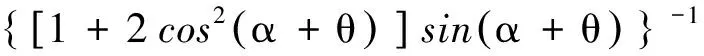
(7)
由表达式已能看出二者速度并非同步变化.可由Mathematica作出二者随绳摆角θ的变化图像,能更形象地表示出二者变化规律.
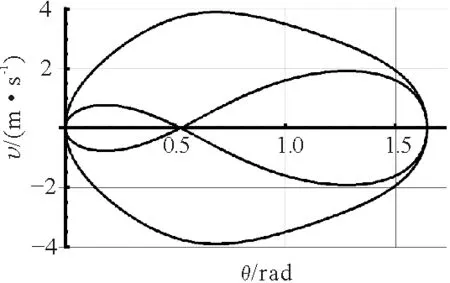
图时两物体速度随绳子摆角变化规律
由图像更能直观看出二者速度变化规律:速度变化并不同步,物块B速度有两个极值,而A只有一个.对于速度极大值的位置可以利用求导的方法进行计算:令速度为θ的函数,并令其导函数为零,求解的根即为速度最大值时对应的绳子摆角.可用Mathematica的寻根命令,解得滑块A速度极大值的位置在θ=0.685 3 rad附近;而物块B速度极值有两个,分别在θ=0.181 4 rad和θ=1.279 9 rad.其中物块B速度为零的位置正是α的余角.


图时两物体速度随绳子摆角变化规律
3 加速度变化规律
由于牵连体在沿着绳子方向上速度相同,即
v2=v1cosα+θ
两边同时对时间求导,得
(8)


v⊥=v1sinα+θ
即有
(9)
将式(9)代入式(8)整合后有
(10)
同时对二者受力分析,如图5所示.

图5 两物体受力示意图
(11)
消去绳子拉力T也可得A,B两物体加速度关系
a1=gsinα+2g-a2cosα+θ
(12)
联立式(10)和式(12),可得加速度表达式
(13)
(14)
将式(6)代入式(13)、(14)即得两物体加速度随绳子摆角变化关系
(15)
(16)
由Mathematica可模拟出二者加速度随摆角之间的变化规律,它们并不同步变化.为了体现与上文的连贯性,我们依然采用以下两个角度加以分析.

图时两物体加速度随绳子摆角变化规律
由图可知:二者在初始时刻加速度并不为零,一起做加速运动,当加速度为零时速度应达到极值,该图像明显反映出滑块A只有一个速度极值,而物块B有两个速度极值,其角度大小与上文所得结果一致.

图时两物体加速度随绳子摆角变化规律
发现在初始一段时间内物块B加速度为负,说明结果与式(10)和式(11)中假设B竖直向下的加速度方向相反:在此种情况下初始时刻B应该是向上加速运动,这也是与事实相吻合的.
4 总结
分析此类复杂的非匀变速运动我们采用了机械能守恒的方法,从而避开了运动过程中变化的受力,相对更简便一些.对于有些牵连体问题,二者速度、加速度并非同步变化,其速度并非同时达到极值,而是有先有后.这就要求教师在教学中对待问题不但要知其然,还要知其所以然,分析原因解决疑难.只有深刻地掌握物理模型,才能在今后的教学中收放自如.
1 王波.探析绳连体模型的加速度关系.物理教师,2011,32(3):41~43
2 闫峰.对连接体最大速度位置的分析.物理教师,2016,37(9):88~89
3 姜付锦.MathCAD在连接体问题研究中的应用.物理通报,2011(12):75~78
