无限长直电流对共面圆电流的安培力
2018-03-27邹俊峻
邹俊峻
(长安大学汽车学院 陕西 西安 710064)
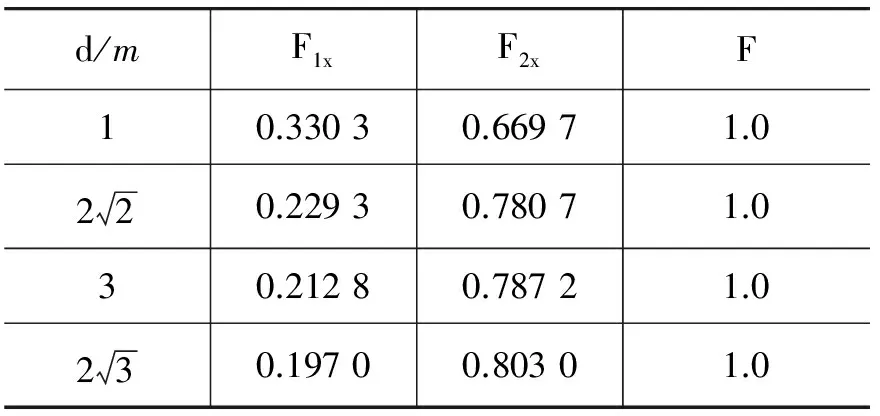
文献[1]中给出了过圆心的无限长直线电流对共面圆形电流的安培力的习题.文献[2]中给出了d=0(过圆心)和d>R(不过圆心)两种情况下,共面的无限长直线电流对圆形电流的安培力,但该题的习题解答[3]中关于数学积分的部分没有写出详细过程,学生在求解这个积分时常常遇到困难.本文利用高等数学知识,对d>R和d 【题目】如图1[2]所示,已知半径为R的平面圆形线圈中载有电流I2,另一无限长直导线AB中载有电流I1,且平面圆形线圈与长直导线AB共面,求圆形电流所受作用力? 图1 d >R时圆形电流的安培力 如图1所示,建立直角坐标系xOy,先分析右边半圆形电流受到的安培力,在右边半圆形电流的P点取电流元I2dl,由安培环路定理可得:长直电流I1在P点处所产生的磁感应强度大小为 (1) 方向垂直纸面向里.电流元I2dl所受安培力大小为 (2) 方向沿半径向外.在x轴下方取Q点,Q点与P点关于x轴对称,并在Q点取相同大小的电流元I2dl′,由对称性可知电流元I2dl和I2dl′所受的安培力关于x轴对称,其y轴分量相互抵消,x轴分量同向且等量.所以右半圆受到的安培力大小为 (3) 方向沿x轴正方向. 同理可得:左边半圆形电流受到的安培力大小为 (4) 方向沿x轴负方向. 所以圆形电流所受安培力的大小为 F=F1x-F2x=μ0I1I2- (5) (6) 令 其分母有两个一阶零点 (7) 因此式(6)的积分为 (8) 同理可得式(5)中第二项积分为 (9) 将式(8)和式(9)代入式(5),得整个圆形电流所受安培力的大小为 (10) 式(10)中F<0,表示合力方向沿x轴负方向.此结果与文献[1~3]是一致的,但本文给出了详细的数学推导过程. 如图2所示,先分析右边半圆形电流受到的安培力,由式(1)~(3)可知右半圆受到的安培力大小为 (11) 方向沿x轴正方向. 图2 d 由式(4)可得导线AB与y轴之间的两段圆弧电流受到的安培力为 (12) 类似地,可得导线AB左边圆弧电流受到的安培力大小为 (13) 方向沿x轴正方向. 综合式(12)和式(13)可得:左边半圆所受安培力的大小为 (14) 所以整个圆形电流所受安培力的大小为 (15) 代入,则有 (16) (17) 同理可得 (18) 将式(17)、(18)代入式(15),可得整个圆形线圈所受安培力的大小为 (19) 式(19)中F>0,表示合力方向沿x轴正方向,且力F与导线AB位置d无关,恒等于μ0I1I2,也等于无限长直线电流通过圆心时对圆形电流所施加的安培力[1~3].如图2所示,当直线电流从圆心位置向左移动时,d从0→R,F1x因d增大而减小,F2x因d增大而增大,但是F=F1x+F2x会保持不变,如表1所示,在表1中选取4个不同的值分别计算了F1x,F2x和F,结果表明:d增大时F1x会减小,F2x会增大,但F保持不变. 表1 R=4 m时不同d值对应的力 注:表中, 力F1x,F2x,F的单位是μ0I1I2. 综上所述,本文求解了无限长直线电流对共面圆形电流的安培力. 利用恒定磁场的安培环路定理、安培定律和高等数学知识,针对d>R和d 1 吴百诗.大学物理(上册)(第二次修订本).西安:西安交通大学出版社,2004.342~343 2 程守洙,江之永.普通物理学(2)(第5版).北京:高等教育出版社,1998.274 3 周逊选,黄伯坚.新编普通物理解题(修订本).武汉:华中科技大学出版社,2001.329~330 4 四川大学高等数学教研室.高等数学(第4册)(第2版).北京:高等教育出版社,1985.107
1 d >R时圆形电流所受安培力
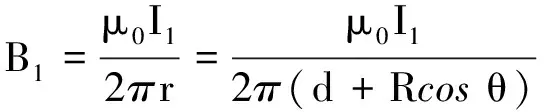

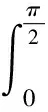
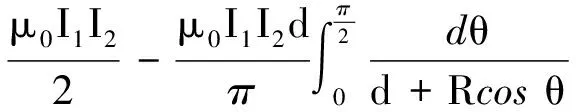


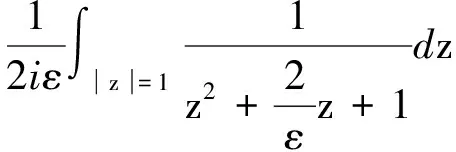

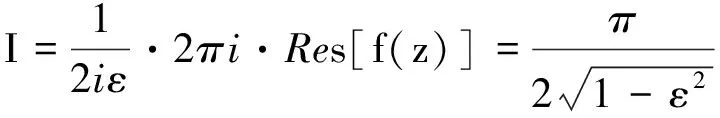
2 d
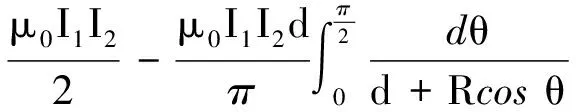


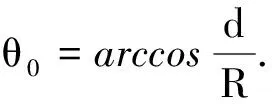
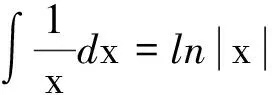
3 结论
