小尺寸单轴应变Si PMOS沟道晶面/晶向选择实验新发现∗

陈航宇 宋建军 张洁 胡辉勇 张鹤鸣

(西安电子科技大学微电子学院,宽禁带半导体材料与器件重点实验室,西安 710071)(2017年9月27日收到;2017年12月19日收到修改稿)

1 引 言

单轴应力作用下,Si能带结构发生变化,空穴迁移率获得增强.单轴应变Si应用于小尺寸沟道p型金属氧化物半导体(PMOS)时,器件性能显著提升,是延续摩尔定律的重要技术手段[1−10].小尺寸单轴应变Si PMOS沟道反型层迁移率与晶面/晶向密切相关,优化设计器件时应选择合理的晶面/晶向[11−14].目前,有关单轴应变PMOS沟道反型层迁移率晶面/晶向排序结论已有相关文献[15]报道(见图1).

图1(a)—(c)为弛豫情况下Si PMOS反型层载流子迁移率随晶面/晶向变化图,当未施加应力时,Si PMOS反型层的空穴迁移率排序为(110)＞(111)＞(001),最大的空穴迁移率出现在(110)晶面沿[10]晶向的沟道方向. 图1(d)—(f)为应力作用下的情况,由图可见,1.5 GPa压应力作用下,(001)晶面的[110]晶向迁移率增强倍数最大,约为弛豫情况下的3倍;(110)晶面与(111)晶面迁移率增强幅度相接近,约为弛豫情况下的两倍.即应力作用下(001)晶面的增强幅度最大;然而,因为弛豫情况下(110)晶面的[10]晶向空穴迁移率最大,即基数最大,而(001)晶面的迁移率最小,在(110)晶面[10]晶向迁移率增大两倍的情况下仍然大于(001)晶面的[110]晶向增强3倍的情况.故该研究还表明,最大空穴迁移率出现在(110)晶面的[10]晶向.

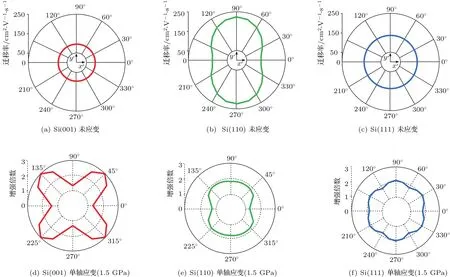
图1 弛豫Si反型层载流子迁移率与单轴应变反型层载流子迁移率增强图Fig.1.Inversion layer mobility for unstrained Si and inversion layer mobility enhancement for uniaxial strain.

值得注意的是:一方面,以上文献[15]报道仅为理论预测排序结果,尚未见涉及全部晶面/晶向排序验证的实验结论;另一方面,沟道受力为1.5 GPa应力强度,是以上文献[15]结论的前提条件,但在实际制作过程中无法引入1.5 GPa的压应力.这就意味着该理论排序模型还具有局限性.

我们知道,小尺寸应变Si PMOS器件沟道应力是通过其上方源区、漏区及栅覆盖SiN应力膜而引入的.SiN疏松膜具有膨胀的趋势,疏松的SiN膜使得PMOS源/漏区域Si材料发生扩张形变,源/漏区域扩张形变进一步引起了沟道区Si材料发生收缩形变.这样,虽然疏松结构SiN膜未直接接触PMOS沟道区域,仍然对沟道区施加了压应变[10,16,17].为了便于理解,该应力引入机理示意图如图2.

在器件实际制造过程中,由于SiN膜淀积工艺固定,而Si材料弹性劲度系数又具有各向异性,当PMOS器件沟道选用不同晶面/晶向时,不同晶面/晶向应变PMOS沟道所受应力强度将不同,由于工艺因素间接导致上述文献[15]沟道反型层迁移率晶面/晶向排序理论模型“失效”.

有鉴于此,本文选用(001),(110),(111)三个典型高对称晶面Si衬底,利用器件平面工艺,并覆盖淀积SiN应力膜,制备不同晶面/晶向40 nm沟道小尺寸单轴应变Si PMOS.通过测试所制备的PMOS样品的转移特性曲线,获取小尺寸单轴应变Si PMOS反型层迁移率晶面/晶向排序的实验结论,并对本文实验排序结果与文献[15]理论预测排序结果予以比对说明.

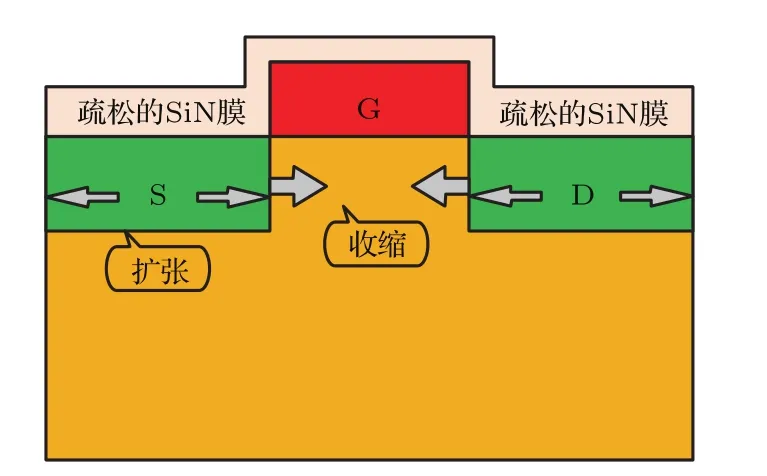
图2 SiN膜结构与PMOS沟道应力类型对应关系Fig.2.Relationship between SiN film and the type of stress in PMOS channel.

本文有关小尺寸单轴应变Si PMOS沟道反型层迁移率晶面/晶向排序的相关结论,由于考虑了工艺实现因素,与文献[15]理论预测排序结果相比,可更适于指导实际工艺制备.同时,本文相关分析方法也可为其他应变材料沟道MOS的设计与制备提供重要技术参考.

2 实验过程

单轴压应变Si PMOS典型的结构示意图见图3,在传统平面工艺制造好PMOS之后,其沟道压应力是通过在源漏区上方淀积疏松的SiN薄膜而引入的.

为研究不同晶面/晶向载流子迁移率的大小排序,首先进行实验方案的确定.本文采用中国科学院微电子研究所40 nm单轴应变Si PMOS工艺,工艺流程如图4所示.

依据晶体极射赤面投影图进一步确定沟道晶面/晶向[18],利用图5所示晶体极射赤面投影图各晶向之间的角度关系,并参考Si晶圆定位边晶向,通过旋转角度,即可确定出不同晶面沟道的各个晶向.

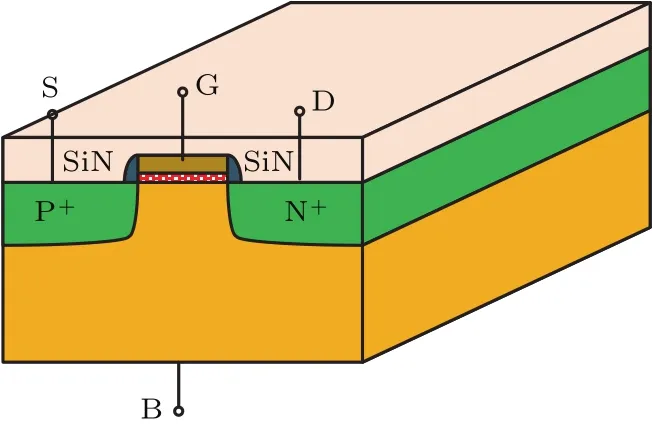
图3 单轴压应力Si PMOS结构示意图Fig.3.Schematic structure of uniaxial strained Si PMOS device.

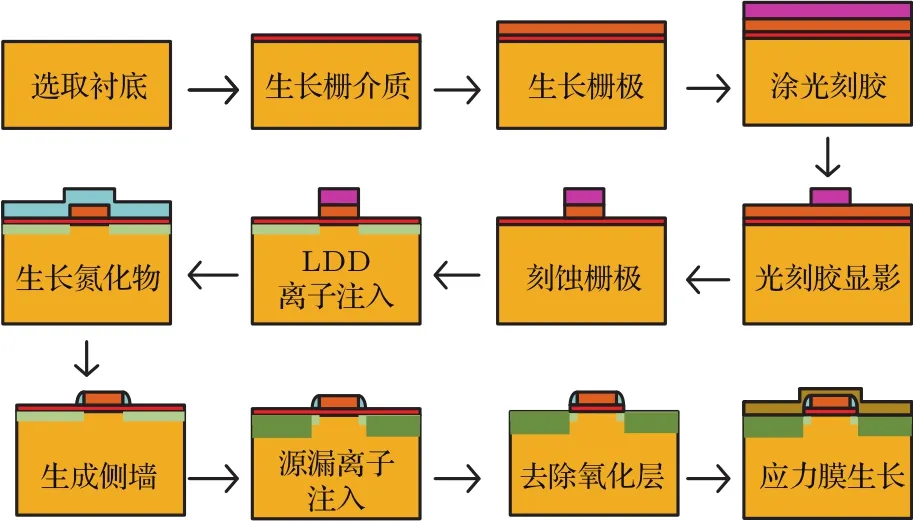
图4 器件制备工艺流程图Fig.4.Flow chart of device manufacturing.

图5 不同晶面极射赤面投影图 (a)(001)晶面;(b)(110)晶面;(c)(111)晶面Fig.5.Stereographic projection for different crystal planes:(a)(001);(b)(110);(c)(111).

Si晶体具有对称性,0°—90°可作为一个周期单元,即可代表所有的晶向.如图5(a)(001)晶面上0°对应[010]晶向,45°对应[110]晶向,90°对应[100]晶向;图5(b)(110)晶面上0°对应[001]晶向,90°对应[10]晶向;图5(c)(111)晶面0°对应[11]晶向,90°对应 [10]晶向.

基于以上讨论,本文确定应变PMOS沟道晶面/晶向方案为:在(001),(110),(111)三个不同晶面晶圆上,分别制作弛豫情况与应力作用下沟道角度为0°—90°范围的晶体管(以15°为一个间隔).其中,(001)晶面相较其他晶面对称性更高,我们选择制备了沟道角度为45°—90°范围的晶体管.图6为所制备的PMOS的一组显微照片(以应变(110)晶面为例,其他晶面以及弛豫情况显微照片与之类似).

利用4200-SCS半导体特性分析系统对上述所制备的不同角度晶体管进行转移特性曲线测试,获得实验数据,并绘制不同晶面/晶向弛豫情况与压应力作用下的转移特性曲线.

3 结果与讨论

利用饱和区漏电流公式(1),可以间接得出载流子迁移率的大小:

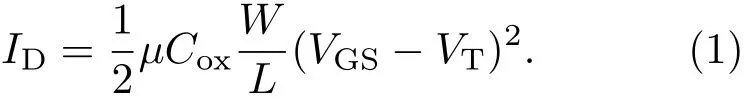
在同一工艺下,不同晶向栅氧化层电容Cox与宽长比W/L相同,忽略应力对于阈值电压VT的影响,则在同一栅极电压情况下,电流大小仅与反型层空穴迁移率µ相关.因此通过器件转移特性曲线,比较不同角度的电流大小即可得出不同角度即不同晶向的迁移率大小.

图7所示为(001)晶面弛豫情况与压应力作用下不同角度的PMOS转移特性曲线.通过对转移特性曲线的提取分析,获得栅压为−1 V时的不同沟道角度的漏极电流大小如图8,进而可得到(001)晶面不同晶向反型层载流子迁移率的排序如表1.

图7 (001)晶面转移特性曲线 (a)弛豫情况;(b)单轴应力作用Fig.7.Transfer characteristic curve of(001)crystal plane:(a)Relaxation;(b)uniaxial strained.

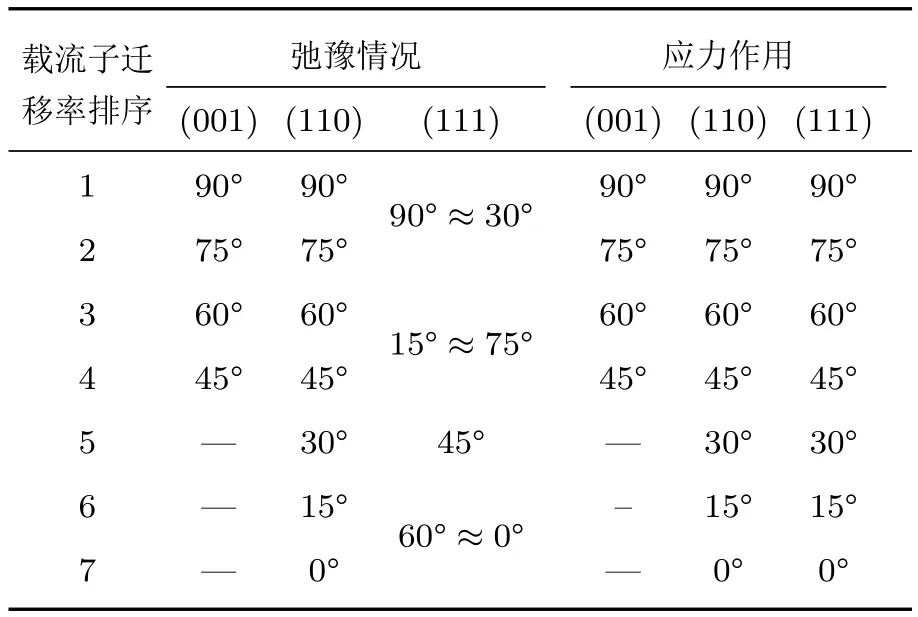
表1 不同晶面/晶向反型层载流子迁移率排序表Table 1.Sort table of inversion layer mobility on different crystal planes/orientation.

结合图7(a)与图8可以得出:弛豫情况下PMOS沟道角度从45°至90°的转向过程中,漏极电流逐渐增大,即对应载流子迁移率逐渐增大.弛豫情况下(001)晶面反型层等能图如图9(a),[110]晶向对应沟道角度为45°的PMOS空穴有效质量最大,其载流子迁移率最小;[100]晶向对应沟道角度为90°的PMOS空穴有效质量最小,其载流子迁移率最大.但由于考虑等能图为双椭球模型[19],故[110]晶向与[010]晶向载流子有效质量虽有差距,但差距不大,因而弛豫情况下载流子迁移率排序与理论报道差距不大.

图8 −1 V栅压下(001)晶面弛豫与应力作用下漏极电流与沟道角度的关系Fig.8.Relationship between drain current and channel angel under the in fl uence of relaxation or stress on(001)crystal plane at−1 V gate voltage.

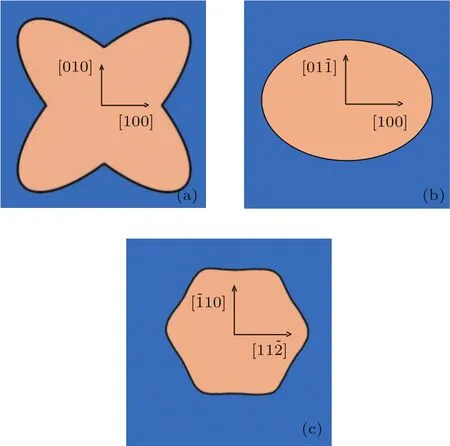
图9 弛豫情况下不同晶面反型层等能图 (a)(001);(b)(110);(c)(111)Fig.9. Equal-energy surfaces of different crystal planes of inversion layer under the in fl uence of relaxation:(a)(001);(b)(110);(c)(111).

结合图7(b)与图8可以得出:压应力作用下,(001)晶面载流子迁移率排序与弛豫情况下的排序相同,仍为90°最高,45°最低;但是不同角度载流子迁移率较弛豫情况下有很大提升,增强倍数各不相同,90°时增强倍数最高,45°增强倍数最小,这是由于Si材料弹性劲度系数具有各向异性,在同种工艺淀积SiN应力膜时,不同晶向沟道上所反映出的应力大小各不相同.

图10为弛豫情况与压应力作用下(110)晶面不同角度的PMOS转移特性曲线,通过对转移特性曲线的提取分析可知:弛豫情况与应力作用下(110)晶面随着角度的递增,其漏电流逐渐增大,栅压为−1 V时的不同沟道角度的漏极电流大小如图11,进而可得到(110)晶面不同晶向反型层载流子迁移率的排序如表1.

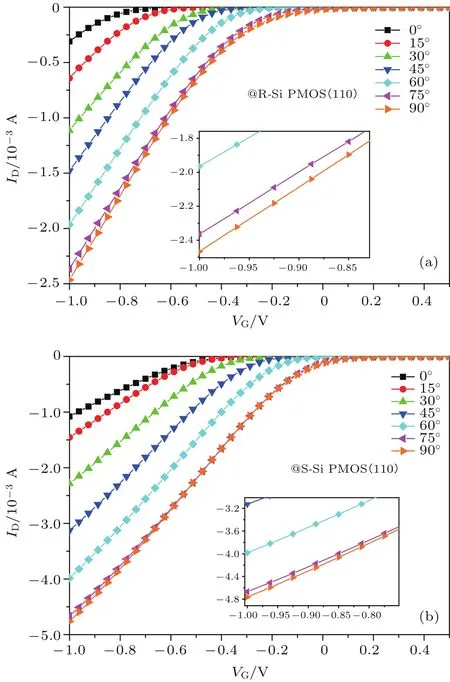
图10 (110)晶面转移特性曲线 (a)弛豫情况;(b)单轴应力作用Fig.10.Transfer characteristic curve of(110)crystal plane:(a)Relaxation;(b)uniaxial strained.

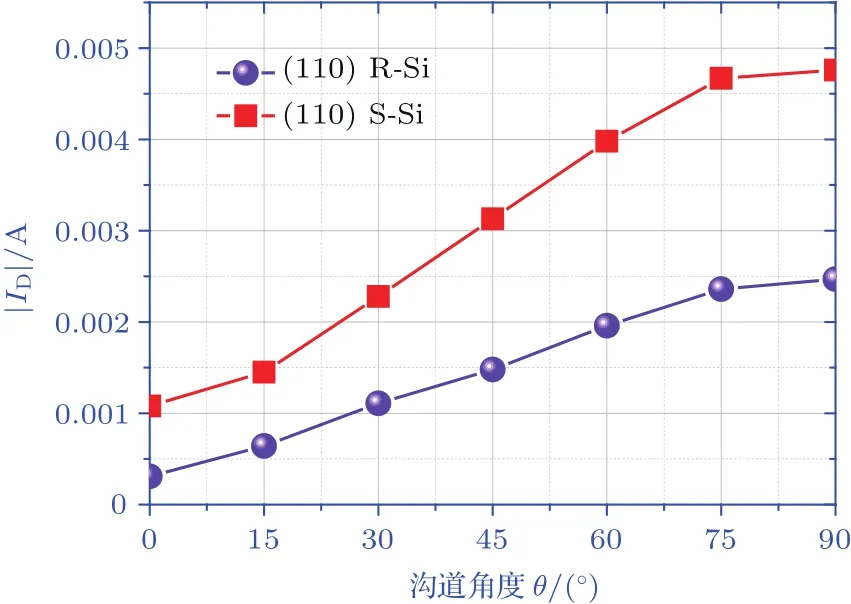
图11 −1 V栅压下(110)晶面弛豫与应力作用下漏极电流与沟道角度的关系Fig.11.Relationship between drain current and channel angel under the in fl uence of relaxation or stress on(110)crystal plane at−1 V gate voltage.

图12为弛豫情况与压应力作用下(111)晶面不同角度的PMOS转移特性曲线,通过对转移曲线提取分析,获得栅压为−1 V时的不同沟道角度的漏极电流大小如图13,进而可得到(111)晶面不同晶向反型层载流子迁移率的排序如表1.

结合图12(a)与图13可以得出:弛豫情况下,(111)晶面90°与30°晶向其漏电流大小接近,15°与75°晶向漏电流大小接近,0°与60°晶向漏电流大小接近,进而得出90°与30°晶向反型层载流子迁移率大小接近,15°与75°次之,45°较小,0°与60°最小.通过对比(111)晶面弛豫情况下的反型层等能图,如图9(c),可以得出0°与60°晶向、15°与75°晶向、30°与90°晶向为对称晶向,其载流子有效质量相同,则理论上其载流子迁移率相同,与本文实验中得到的结论相符,亦与理论报道相接近.从(111)晶面弛豫情况下的反型层等能图还可以发现各个晶向载流子有效质量相差不大,所以各个晶向载流子迁移率不会有大的差距.进而得到弛豫情况下(111)晶面 [10]晶向载流子迁移率稍大于 [11]晶向载流子迁移率.

图12 (111)晶面转移特性曲线 (a)弛豫情况;(b)单轴应力作用Fig.12.Transfer characteristic curve of(111)crystal plane:(a)Relaxation;(b)uniaxial strained.

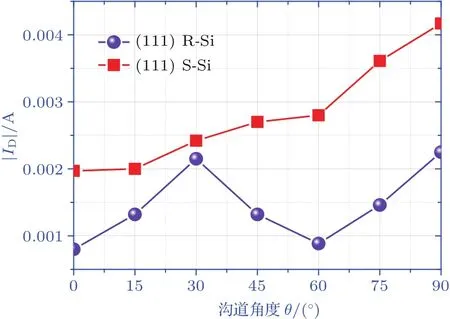
图13 −1 V栅压下(110)晶面弛豫与应力作用下漏极电流与沟道角度的关系Fig.13.Relationship between drain current and channel angel under the in fl uence of relaxation or stress on(111)crystal plane at−1 V gate voltage.

结合图12(b)与图13可以得出:压应力作用下,从0°到90°晶向的转动过程中,漏电流逐渐增加,即相应载流子的迁移率逐渐增加,90°对应的[10]晶向载流子迁移率最大,0°对应的 [11]晶向载流子迁移率最小.与理论上的排序结果不符,主要原因在于应力作用下,由于其弹性劲度系数具有各向异性,所以在(111)晶面上不同晶向所对应的沟道上所受的应力并不相同,[10]晶向沟道所受的压应力相对其他晶向的大,而[11]晶向沟道所受的压应力最小.但是在理论分析过程中默认在(111)晶面上不同晶向所对应的沟道所受应力大小相等.

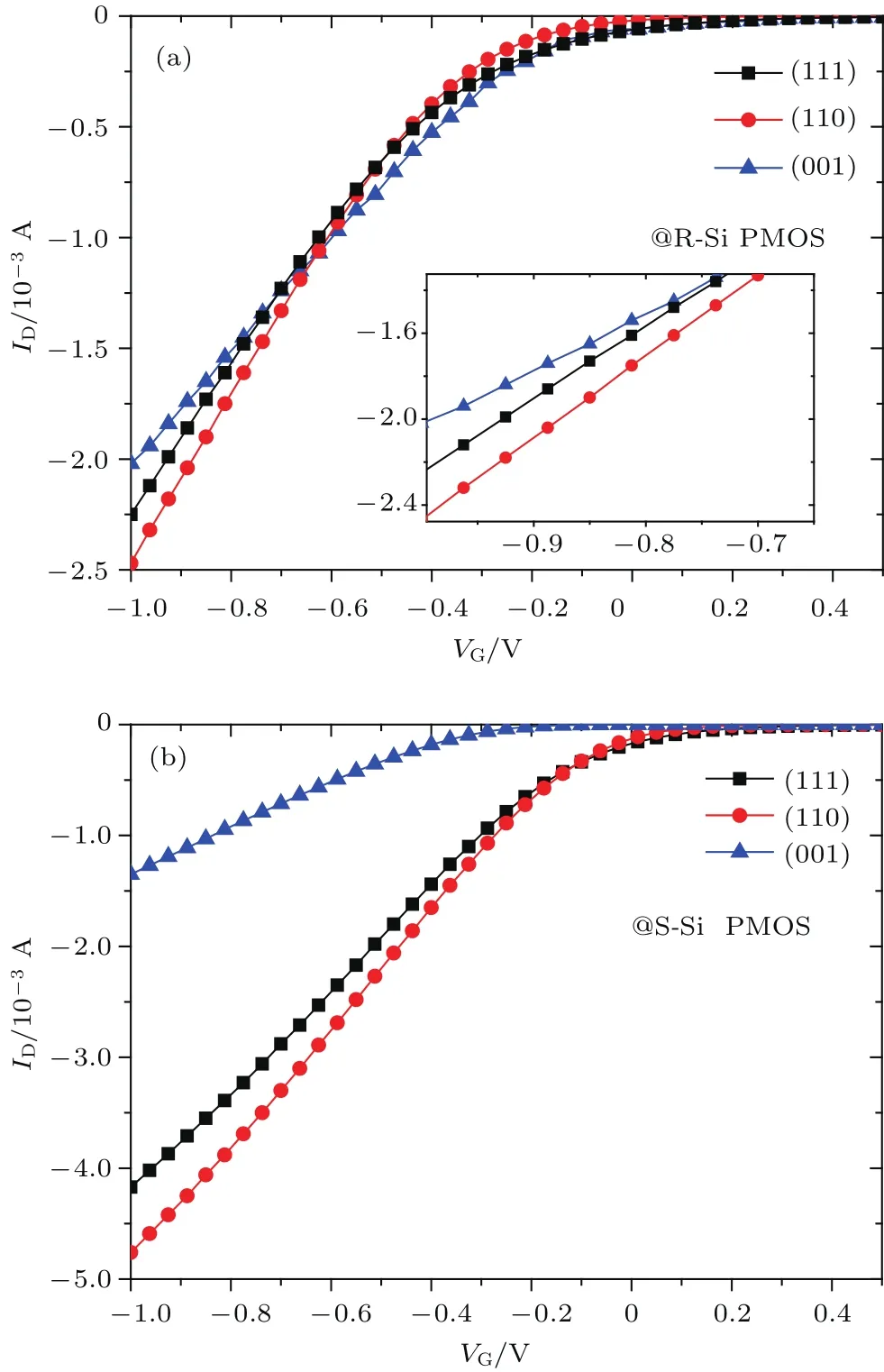
图14 90°沟道下不同晶面转移特性曲线 (a)弛豫情况;(b)单轴应力作用Fig.14.Transfer characteristic curve of 90°channel on different crystal planes:(a)Relaxation;(b)uniaxial strained.

在之前的讨论中可以得到,弛豫与压应力情况下,沟道角度为90°时对应不同晶面的最大迁移率.通过比较不同晶面90°沟道下的转移特性曲线,如图14,可以得出:弛豫情况下载流子迁移率排序为(110)＞(111)＞(001),载流子迁移率最大值出现在(110)晶面的90°沟道下;应力作用下,载流子迁移率排序为(110)＞(111)＞(001),载流子迁移率最大值同样出现在(110)晶面的90°沟道下,即在压应力条件下最大迁移率为(110)晶面的[10]晶向上.

通过在同一工艺下对实验所制备的小尺寸压应力下Si PMOS进行测试,得到实验与理论情况下,压应力作用时不同晶面反型层载流子迁移率排序对比表如表2,可以看出,实验情况与理论分析有些许出入,这主要是由于晶体的弹性劲度系数具有各向异性,在同一实验环境下,淀积相同的SiN应力膜时,不同晶向沟道上所反映出的压应力大小不同.

为进一步说明实验结果,采用(001)晶面不同晶向的器件进行反型层载流子迁移率的验证,通过计算得到弛豫情况下,(001)晶面90°方向,即[100]晶向,载流子迁移率约为82 cm2/(V·s);而(001)晶面45°方向,即[110]晶向,载流子迁移率约为80 cm2/(V·s).这与理论情况相接近,文献[15]理论报道中弛豫情况下(001)晶面不同晶向反型层载流子迁移率大小一致,约为87 cm2/(V·s).

表2 应力作用下PMOS反型层载流子迁移率对比Table 2.Comparative table of inversion layer mobility of Si PMOS under stress.

应力作用下,实际测得(001)晶面90°方向,即[100]晶向,载流子迁移率约为136 cm2/(V·s);而(001)晶面45°方向,即[110]晶向,载流子迁移率约为115 cm2/(V·s).[100]晶向反型层载流子迁移率增强幅度约为1.66倍,[110]晶向反型层载流子迁移率增强幅度约为1.44倍,这与文献[15]结果相差较大,其原因在于文献[15]中采用了1.5 GPa单轴应力,而在实际工艺中利用氮化硅膜无法引入这么大的应力,并且晶体弹性劲度系数具有各向异性,使得文献[15]结果与实验结果具有不统一之处,因此结果合理.

4 结 论

本文通过实验系统验证了小尺寸单轴应变Si PMOS不同晶面/晶向载流子的迁移率变化,并与理论相对比,得出了在工业制造中的具体情况下不同晶面/晶向载流子的迁移率排序.

在本实验工艺条件下,小尺寸单轴应变Si PMOS反型层载流子迁移率排序表面上与理论计算看似不统一.一方面是由于理论计算时设定不同晶面、不同晶向所受到的压应力大小相同,均为1.5 GPa,而在工业生产中应变PMOS器件中引入的压应力大小为1.0 GPa,无法引入1.5 GPa的压应力;另一方面是由于晶体存在弹性劲度系数矩阵,因此对于Si晶体而言其弹性劲度系数具有各向异性,当使用同一工艺淀积SiN应力膜时,不同晶向沟道上所反映出的应力大小将会有所不同,而这将会导致不同晶向上载流子迁移率的增强倍数各不相同,因此产生了实验结果与理论分析不统一的情况.

本文实验情况由于考虑到实际工艺的影响,给出了所有晶面/晶向的反型层载流子迁移率排序,所得出的反型层载流子迁移率新排序可为实际器件的制造提供具有指导性的参考,同时为其他应变材料的分析提供了一种新的思路.

[1]Guan H,Guo H 2017Chin.Phys.B26 058501

[2]Theerani J T 2017IEEE Trans.Electron Dev.64 3316

[3]Bai M,Xuan R X,Song J J,Zhang H M,Hu H Y,Shu B 2015Comput.Theor.Nanos12 1610

[4]Hao M R,Hu H Y,Liao C G,Wang B,Zhao X H,Kang H Y,Su H,Zhang H M 2017Acta Phys.Sin.66 076101(in Chinese)[郝敏如,胡辉勇,廖晨光,王斌,赵小红,康海燕,苏汉,张鹤鸣2017物理学报66 076101]

[5]Song J J,Yang C,Zhu H,Zhang H M,Xuan R X,Hu H Y,Shu B 2014Acta Phys.Sin.63 118501(in Chinese)[宋建军,杨超,朱贺,张鹤鸣,宣荣喜,胡辉勇,舒斌2014物理学报63 118501]

[6]Liu W F,Song J J 2014Acta Phys.Sin.63 238501(in Chinese)[刘伟峰,宋建军 2014物理学报 63 238501]

[7]Lee C H,Southwick R G,Bao R,Mochizuki S,Paruchuri V,Jagannathan H 2017Symposia on VLSI TechnologyKyoto,Japan,June 5–8,2017 p126

[8]Li L,Liu H X,Yang Z N 2012Acta Phys.Sin.61 166101(in Chinese)[李立,刘红侠,杨兆年 2012物理学报 61 166101]

[9]Kasim J,Reichel C,Dilliway G,Bai B,Zakowsky N 2015Solid-State Electronics110 19

[10]Huang H L,Chen J K,Houng M P 2013Solid-State Electron.79 31

[11]Wang X Y 2012Ph.D.Dissertation(Xi’an:Xidian University)(in Chinese)[王晓艳 2012博士学位论文 (西安:西安电子科技大学)]

[12]Dai X Y,Yang C,Song J J,Zhang H M,Hao Y,Zheng R C 2012Acta Phys.Sin.61 137104(in Chinese)[戴显英,杨程,宋建军,张鹤鸣,郝跃,郑若川2012物理学报61 137104]

[13]Wang G Y,Song J J,Zhang H M,Hu H Y,Ma J L,Wang X Y 2012Acta Phys.Sin.61 097103(in Chinese)[王冠宇,宋建军,张鹤鸣,胡辉勇,马建立,王晓艳2012物理学报61 097103]

[14]Zhang W H,Li Z C,Guan Y H,Zhang Y F 2017Chin.Phys.B26 078502

[15]Krishnamohan T,Kim D,Dinh T V,Pham A,Meinerzhagen B,Jungemann C,Saraswat K 2008Electron Devices MeetingSan Francisco,CA,USA,December 15–17,2008 p1

[16]Cai W L,Takenaka M,Takagi S 2014J.Appl.Phys.115 094509

[17]Yang M Y,Song J J,Zhang J,Tang Z H,Zhang H M,Hu H Y 2015Acta Phys.Sin.64 238502(in Chinese)[杨旻昱,宋建军,张静,唐召唤,张鹤鸣,胡辉勇 2015物理学报64 238502]

[18]Song J J 2008Ph.D.Dissertation(Xi’an:Xidian University)(in Chinese)[宋建军 2008博士学位论文 (西安:西安电子科技大学)]

[19]Song J J,Bao W T,Zhang J,Tang Z H,Tan K Z,Cui W,Hu H Y,Zhang H M 2016Acta Phys.Sin.65 018501(in Chinese)[宋建军,包文涛,张静,唐昭焕,谭开洲,崔伟,胡辉勇,张鹤鸣2016物理学报65 018501]