基于自发参量下转换源二阶激发过程产生四光子超纠缠态∗

何英秋 丁东 彭涛 闫凤利 高亭

1)(承德医学院生物医学工程系,承德 067000)

2)(华北科技学院理学院,北京 101601)

3)(河北师范大学物理科学与信息工程学院,石家庄 050024)

4)(河北师范大学数学与信息科学学院,石家庄 050024)

1 引言

在光量子信息处理中,量子比特对应的实际物理系统是由光子构成的光学系统[1,2],其中最简单、最重要的纠缠资源是成对的纠缠光子.作为一种非线性光学过程,自发参量下转换是指一束短脉冲紫外光子入射到非线性晶体BBO(β-barium-borate)上产生两个纠缠光子的现象[3−5],对应的这两个光子分别称为信号光子和休闲光子.自发参量下转换过程分为两类,在第一类中产生的信号光子和休闲光子的偏振方向相同,在第二类中产生的信号光子和休闲光子的偏振方向相互垂直.这里,以第二类自发参量下转换过程为例,其相互作用过程中的哈密顿量为[6,7]

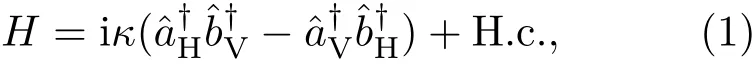
对于自发参量下转换源,除了应用一阶激发过程产生成对的纠缠光子外,其高阶激发同样具有重要的研究意义.一般地,自发参量下转换源高阶激发过程[11−16]对应产生的多光子纠缠态可表示为

其中,|n−m〉aH表示在空间模a中有n−m个H偏振光子,其他项具有类似的意义;τ=κt/ħ是相互作用参数,t是相互作用时间.值得注意的是这里的态表示的是n对不可区分的光子态,不同于n对相互独立的光子对.

一般地,光子可以在偏振、空间和频率等自由度上纠缠.当一个光学系统同时在两个以上自由度上具有纠缠时,通常称之为超纠缠态[17−22].相对于单一自由度上的纠缠态而言,超纠缠态是一种应用更为广泛的纠缠资源,比如可应用于纠缠态分析[23−28]、纠缠纯化和浓缩[29−35]、超并行量子计算[36−38]及超纠缠量子通信[39−42]等.本文研究基于自发参量下转换源二阶激发过程产生四光子超纠缠态方案.方案中,应用线性光学器件设计可行的量子线路,演化参量下转换源激发的四个不可区分的纠缠光子态.最后,基于四光子符合探测,可制备一个同时包含偏振纠缠和空间纠缠的四光子超纠缠态.

2 四光子超纠缠态的制备

这里研究基于二阶自发参量下转换过程制备四光子超纠缠态方案.如图1所示,考虑一个短脉冲紫外光通过BBO晶体,在空间模a1和b1(或空间模a2和b2)激发四个不可区分的纠缠光子,即态

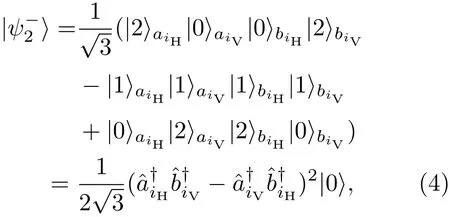
其中,|0〉表示真空态,i=1,2.图1中,分束器的作用是当一个光子通过分束器时其通过和被反射的概率各占50%;半波片的作用是演化光子的偏振状态|H〉到|V〉,或演化状态|V〉到|H〉;偏振分束器的作用是使水平偏振光通过而垂直偏振光被反射.

很明显,二阶自发参量下转换过程激发的四光子纠缠态可能处于空间模a1和b1,当然也可能激发于空间模a2和b2.首先考虑四光子处于空间模a1和b1的情况.由空间模a1,b1到空间模C1,C2,D1和D4,经过两个分束器的作用,光子的演化过程满足

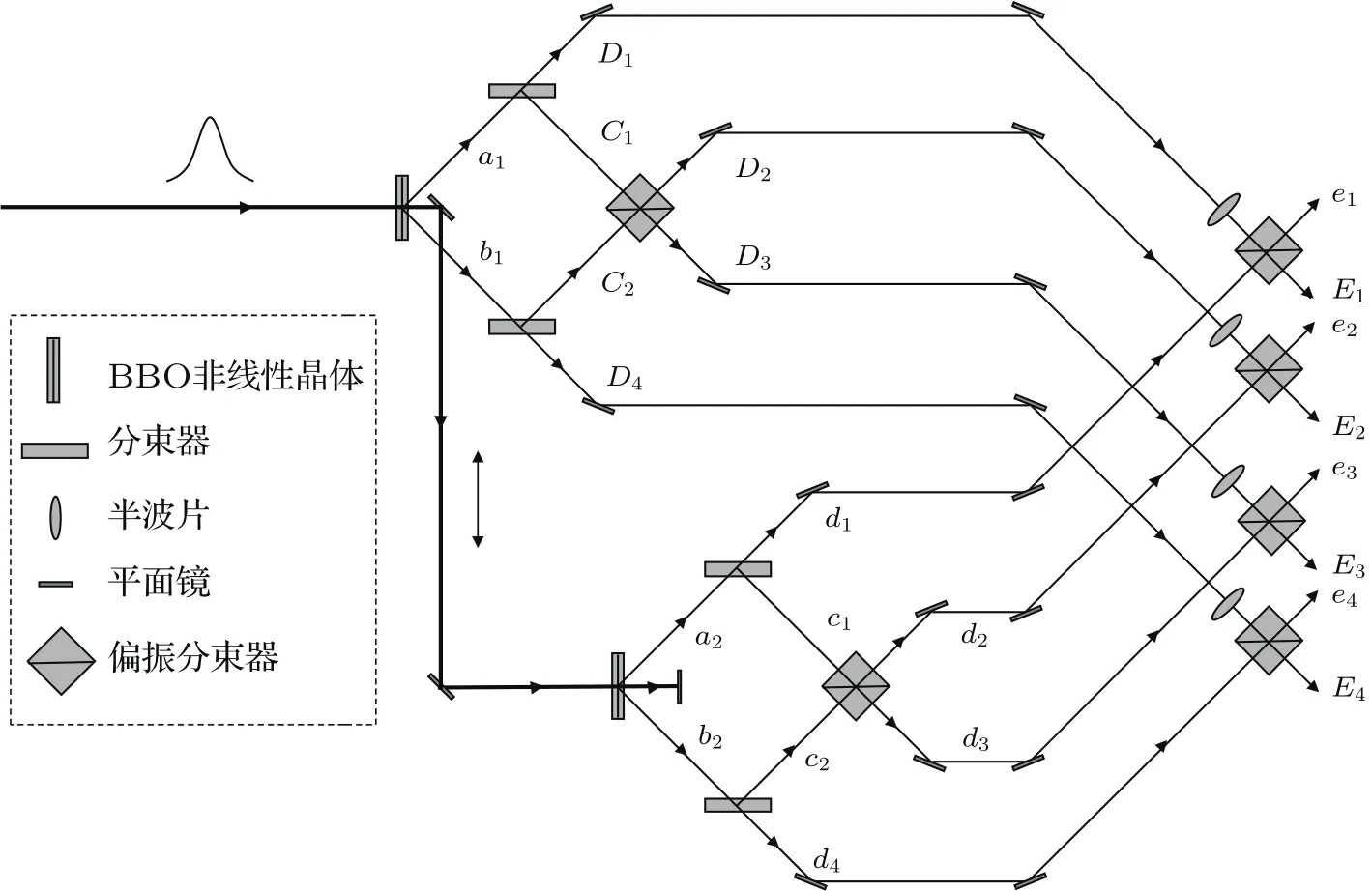
图1 四光子超纠缠态制备原理图Fig.1.The schematic diagram of generating four-photon hyperentangled state.

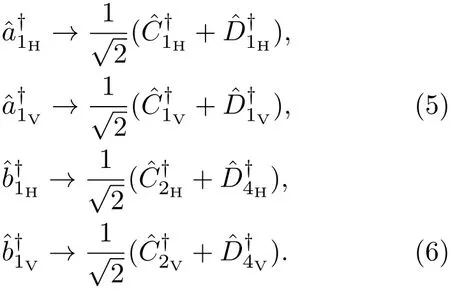
于是,四光子纠缠态演化为

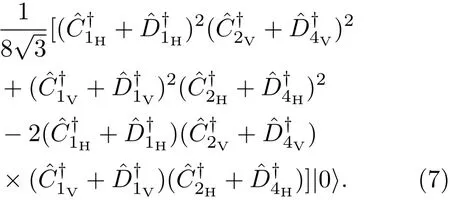
接着,空间模C1和C2中的光子经偏振分束器干涉,满足

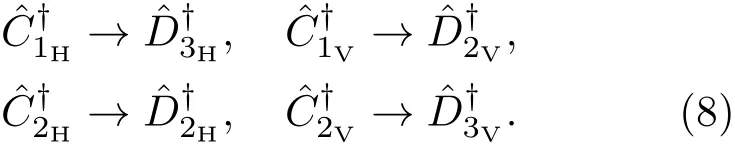
此时,空间模D1,D2,D3和D4中的四光子纠缠态可表示为

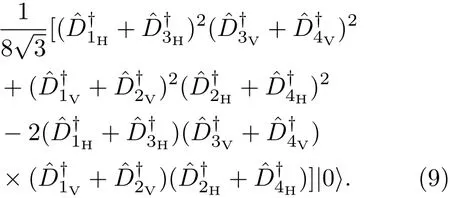
随后,光子经过半波片和偏振分束器作用,即

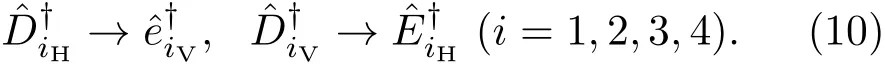
从空间模Di到空间模ei,Ei,其中i=1,2,3,4,四光子纠缠态演化为

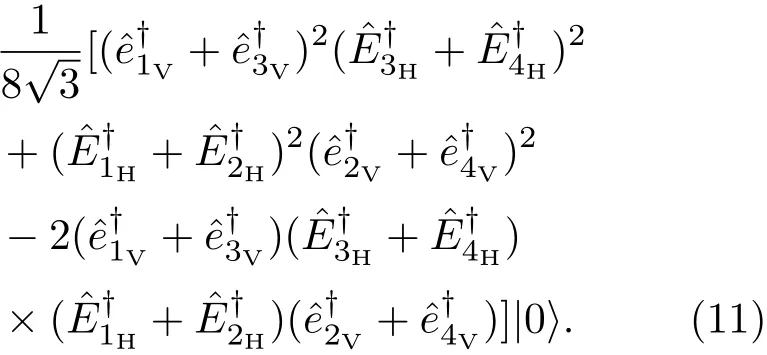
另一方面,考虑自发参量下转换源激发的四光子处于空间模a2和b2的情况.同理,由于空间模a2和b2中两个分束器和空间模c1,c2中偏振分束器的作用,最初激发的四光子纠缠态演化为

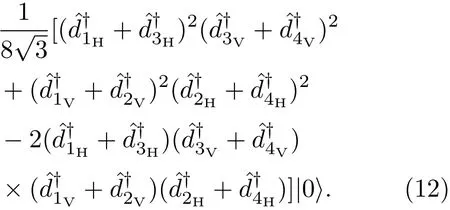
表1 四光子GHZ态的符合探测结果及其对应的概率Table 1.The results of fourfold coincidence detections and the corresponding probabilities for the four-photon GHZ states.

接下来,经过最后这组偏振分束器作用,空间模ei,Ei(i=1,2,3,4)中的四光子纠缠态演化为

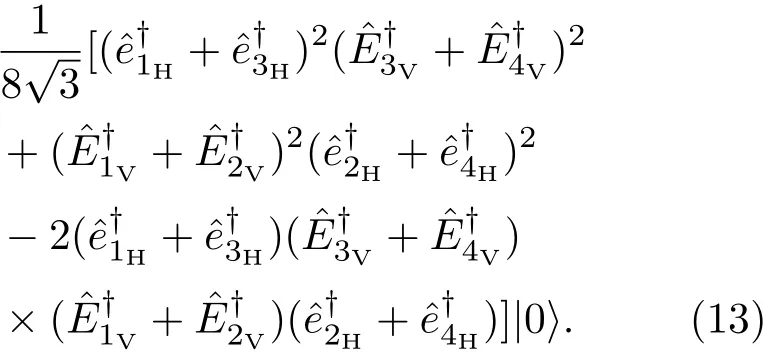
这里,我们假定四个光子处于空间模a1和b1与空间模a2和b2这两种激发状态的概率相同、相对相位为零并且对光子的两种激发状态不进行区分.于是,可以通过选择适当的四模光子符合探测投影四光子态到不同的子空间.考虑四个光子同时出现在不同空间模的情况,此时可以得到人们熟知的四光子GHZ态.具体地,对应于不同的符合探测结果,得到的四光子GHZ态及其对应的概率如表1所列.根据表1中的结果,不难发现基于参量下转换源二阶激发过程得到偏振纠缠四光子GHZ态的总概率为1/2.

另一方面,如果选择不区分空间模ei和Ei(i=1,2,3,4)的四模符合事件,即考虑空间模e1(或E1),e2(或E2),e3(或E3)和e4(或E4) 中有且仅有一个光子的情况,得到态

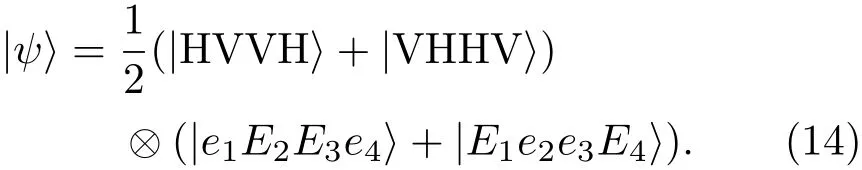
显然,该四光子纠缠态既具有偏振纠缠又有空间纠缠,是超纠缠态.由表1中的结果可知,获得该超纠缠态的概率为1/24.

3 讨 论

基于自发参量下转换源二阶激发过程,我们给出了一个四光子超纠缠态的制备方案.在基于自发参量下转换源一阶激发过程制备四光子超纠缠态方案[31]中,需要引入量子非破坏性测量[43−51]来区分参量下转换源激发的两对纠缠光子所处的状态.而对于仅包含二阶激发过程的自发参量下转换源而言,这里不需要区分四个纠缠光子所处的状态,因此当前方案更具可行性.对于自发参量下转换源同时包含一阶激发和二阶激发过程的情况,因为用于演化四光子系统的量子线路及随后的四光子符合探测选择性地遗弃了一个空间模同时包含两个处于相同偏振状态的光子对应的项,于是,这里得到的态与一阶激发过程中的两对纠缠光子激发于同一空间模的情况相同,所以本文的方案可以提高超纠缠态的制备效率.当前实验上,人们主要通过抑制参量下转换源高阶激发过程,以确保仅产生成对的纠缠光子并进一步实现多光子纠缠态的制备.而实际上,本文的研究表明,对于四光子超纠缠态的制备,自发参量下转换源二阶激发过程不必刻意抑制,而恰恰是可以灵活应用的.同时,我们也注意到自发参量下转换源二阶激发过程的实验观测[12,13,15]、一阶激发与二阶激发间的参数控制[14]以及高阶激发光子的区分[52]等.随着人们对自发参量下转换源高阶激发过程的深入研究,相信其在多光子纠缠态的产生、制备及应用等方面一定有其独特的实际应用价值.

4 结 论

基于自发参量下转换源二阶激发过程,提出了一个简单可行的四光子超纠缠态制备方案.方案中,应用分束器、半波片和偏振分束器等线性光学器件设计量子线路演化参量下转换过程激发的四个不可区分光子.通过四模光子符合探测,四光子态可演化为同时具有偏振纠缠和空间纠缠的超纠缠态.本方案的提出可为应用自发参量下转换源高阶激发过程提供新的思路和方法.

[1]Kok P,Munro W J,Nemoto K,Ralph T C,Dowling J P,Milburn G J 2007Rev.Mod.Phys.79 135

[2]Pan J W,Chen Z B,Lu C Y,Weinfurter H,Zeilinger A,Żkowski M 2012Rev.Mod.Phys.84 777

[3]Burnham D C,Weinberg D L 1970Phys.Rev.Lett.25 84

[4]Kiess T E,Shih Y H,Sergienko A V,Alley C O 1993Phys.Rev.Lett.71 3893

[5]Kwiat P G,Mattle K,Weinfurter H,Zeilinger A 1995Phys.Rev.Lett.75 4337

[6]Kok P,Braunstein S L 2000Phys.Rev.A61 042304

[7]Simon C,Weihs G,Zeilinger A 2000Phys.Rev.Lett.84 2993

[8]Wieczorek W,Schmid C,Kiesel N,Pohlner R,Gühne O,Weinfurter H 2008Phys.Rev.Lett.101 010503

[9]Yao X C,Wang T X,Xu P,Lu H,Pan G S,Bao X H,Peng C Z,Lu C Y,Chen Y A,Pan J W 2012Nat.Photon.6 225

[10]Wang X L,Chen L K,Li W,Huang H L,Liu C,Chen C,Luo Y H,Su Z E,Wu D,Li Z D,Lu H,Hu Y,Jiang X,Peng C Z,Li L,Liu N L,Chen Y A,Lu C Y,Pan J W 2016Phys.Rev.Lett.117 210502

[11]Ou Z Y,Rhee J K,Wang L J 1999Phys.Rev.Lett.83 959

[12]Lamas-Linares A,Howell J,Bouwmeester D 2001Nature412 887

[13]Simon C,Bouwmeester D 2003Phys.Rev.Lett.91 053601

[14]de Riedmatten H,Scarani V,Marcikic I,Acín A,Tittel W,Zbinden H,Gisin N 2004J.Mod.Opt.51 1637

[15]Nagata T,Okamoto R,O’Brien J L,Sasaki K,Takeuchi S 2007Science316 726

[16]Ding D,HeY Q,Yan F L,Gao T 2017 arXiv:1705.00392 [quant-ph]

[17]Kwiat P G 1997J.Mod.Opt.44 2173

[18]Barreiro J T,Langford N K,Peters N A,Kwiat P G 2005Phys.Rev.Lett.95 260501

[19]Vallone G,Ceccarelli R,de Martini F,Mataloni P 2009Phys.Rev.A79 030301

[20]Du K,Qiao C F 2012J.Mod.Opt.59 611

[21]Ding D,He Y Q,Yan F L,Gao T 2015Acta Phys.Sin.64 160301(in Chinese)[丁东,何英秋,闫凤利,高亭2015物理学报64 160301]

[22]Deng F G,Ren B C,Li X H 2017Sci.Bull.62 46

[23]Walborn S P,Pádua S,Monken C H 2003Phys.Rev.A68 042313

[24]Wei T C,Barreiro J T,Kwiat P G 2007Phys.Rev.A75 060305

[25]Sheng Y B,Deng F G,Long G L 2010Phys.Rev.A82 032318

[26]Ren B C,Wei H R,Hua M,Li T,Deng F G 2012Opt.Express20 24664

[27]Li X H,Ghose S 2016Phys.Rev.A93 022302

[28]Xia Y,Chen Q Q,Song J,Song H S 2012J.Opt.Soc.Am.B29 1029

[29]Sheng Y B,Deng F G 2010Phys.Rev.A81 032307

[30]Ren B C,Long G L 2014Opt.Express22 6547

[31]He Y Q,Ding D,Yan F L,Gao T 2015J.Phys.B:At.Mol.Opt.Phys.48 055501

[32]Ren B C,Du F F,Deng F G 2014Phys.Rev.A90 052309

[33]Du F F,Li T,Long G L 2016Ann.Phys.375 105

[34]Liu H J,Xia Y,Song J 2016Quantum Inf.Process.15 2033

[35]Ren B C,Wang H,Alzahrani F,Hobiny A,Deng F G 2017Ann.Phys.385 86

[36]Ren B C,Wang G Y,Deng F G 2015Phys.Rev.A91 032328

[37]Li T,Long G L 2016Phys.Rev.A94 022343

[38]Wei H R,Deng F G,Long G L 2016Opt.Express24 18619

[39]Wang T J,Song S Y,Long G L 2012Phys.Rev.A85 062311

[40]Sheng Y B,Zhou L 2015Sci.Rep.5 7815

[41]Jiang Y X,Guo P L,Gao C Y,Wang H B,Alzahrani F,Hobiny A,Deng F G 2017Sci.China:Phys.Mech.Astron.60 120312

[42]Wu F Z,Yang G J,Wang H B,Xiong J,Alzahrani F,Hobiny A,Deng F G 2017Sci.China:Phys.Mech.Astron.60 120313

[43]Nemoto K,Munro W J 2004Phys.Rev.Lett.93 250502

[44]Munro W J,Nemoto K,Beausoleil R G,Spiller T P 2005Phys.Rev.A71 033819

[45]Barrett S D,Kok P,Nemoto K,Beausoleil R G,Munro W J,Spiller T P 2005Phys.Rev.A71 060302

[46]Lin Q,He B,Bergou J A,Ren Y H 2009Phys.Rev.A80 042311

[47]Ding D,Yan F L 2013Phys.Lett.A377 1088

[48]Ding D,Yan F L,Gao T 2014Sci.China:Phys.Mech.Astron.57 2098

[49]He Y Q,Ding D,Yan F L,Gao T 2015Opt.Express23 21671

[50]Zhou L,Sheng Y B 2015Phys.Rev.A92 042314

[51]Sheng Y B,Pan J,Guo R,Zhou L,Wang L 2015Sci.China:Phys.Mech.Astron.58 060301

[52]He Y Q,Ding D,Yan F L,Gao T 2017Sci.Rep.7 15356