基于金刚石色心自旋磁共振效应的微位移测量方法∗
2018-03-26王磊郭浩陈宇雷伍大锦赵锐刘文耀李春明夏美晶赵彬彬朱强唐军刘俊
王磊 郭浩 陈宇雷 伍大锦 赵锐 刘文耀李春明 夏美晶 赵彬彬 朱强 唐军 刘俊
1)(中北大学,仪器科学与动态测试教育部重点实验室,太原 030051)
2)(中北大学,仪器与电子学院,太原 030051)
1 引 言
原子力显微系统、扫描探针显微系统等精密测量仪器通过其纳米级扫描探针装置,能够实现纳米操控和对纳米区域、纳米结构的表面探测[1−3].随着纳米科技、精密探测等技术的不断发展,基于高分辨率、高精度微位移测量系统的纳米级扫描探针技术在表面科学、材料科学、生命科学等各个领域发挥着越来越重要的作用[4−7].
目前,高分辨率、高精度微位移测量系统主要采用压电陶瓷、微机械结构应力反馈等方法来实现探针系统微位移的精密测量与控制等[8].Liu和Li[9]采用压电陶瓷结构的微驱动特性,利用现场可编程门阵列电压反馈控制方法,研制了高分辨率的微位移测量系统,分辨率达到30 nm.但由于压电陶瓷迟滞、蠕变、非线性的问题,限制了分辨率的提高.Ito等[10]利用Cr-N薄膜结构的高灵敏度应力敏感特性,结合微机械结构微位移作用下的应力反馈检测,实现了对20 nm分辨率的微位移检测.Gather等[11]采用微机械弹性共振结构在微位移作用下产生的应力来反馈检测微位移大小,实现了对2 nm大小的微位移高分辨率检测.然而受限于微机械结构的加工工艺复杂、工艺误差大、重复性差等问题,使其测量分辨率难以进一步提升.因此,需要新型技术来打破传统微位移测量的发展瓶颈.
近年来,以金刚石氮空位色心体系为核心的物理量探测,以其原子自旋和电子自旋效应作为物理量检测的基本原理,成为精密测量技术发展的新方向[12−14].目前,基于金刚石氮空位色心的原子自旋和电子自旋敏感机理的磁强计已经实现了pT量级的磁场检测[15,16].以此磁强计来对磁梯度场中不同位置磁场强度的检测,并通过磁场强度的变化反应位置的改变,由此可以实现对微位移的高分辨率测量.
本文利用金刚石氮空位色心自旋结构对磁梯度场的高精度敏感机理,结合永磁体周围不同位置对应的磁场强度变化关系,提出了一种基于金刚石氮空位色心的电子自旋敏感机理的微位移检测方法,并搭建了相应的微位移测量系统.初步探索了该系统对微位移分辨率,为金刚石氮空位色心在微位移传感领域的研究提供实验基础.
2 实 验
2.1 微位移测量原理
金刚石氮空位(NV)色心是由氮原子取代金刚石晶格中的一个碳原子与相邻的碳空位组成,具有C3υ对称,对称轴为由氮原子和空穴形成的晶轴,称为NV轴,NV轴方向与金刚石[111]晶相方向一致[17,18].是一种典型的电子自旋结构.金刚石NV色心在磁场的作用下,其电子自旋能级发生塞曼分裂,具有超高的磁场分辨能力[19,20],基态能级结构如图1(a)所示.利用金刚石NV色心的电子自旋对磁场的分辨特性,能够实现对磁梯度场的分辨,进而实现对磁梯度场对应的位置测量,以此实现对微位移的检测,其原理如图1所示.
金刚石NV色心的能级基态是自旋三重态,如图1(a)所示,由于两个不成对电子的磁偶极子相互作用,ms=0态和ms=±1态之间存在D=2.87 GHz的零场分裂[21].当无外界磁场的影响时,ms=±1处于简并态(E=0),电子自旋共振(ESR)光谱只有一个共振谷的出现;当受到外界环境的磁场作用时,ms=+1和ms=−1发生退简并,ESR光谱将会出现两个共振谷[22].当外界所施加磁场方向沿金刚石NV色心轴线方向时,共振频率ω可由(1)式表示[16,23]:
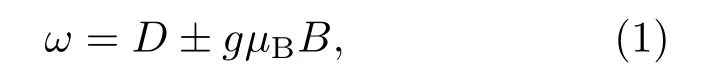
其中B为磁感应强度,µB是玻尔磁子(µB=1.4 MHz/Gauss),g是朗德因子(g=2).塞曼分裂频率Δω与磁感应强度B关系可以表示为


图1 (a)能级图;(b),(c)位移测量原理图Fig.1.(a)Energy level diagram;(b)and(c)the principle of displacement measurement.
永磁体、磁线圈等常规磁体结构周围磁场成梯度场分布[24].文中圆柱形永磁体的材料为N35烧结钕铁硼,沿轴线方向均匀磁化,其磁化强度M为0.1229 T,尺寸半径r=8×10−3m,高度h=1×10−3m.以圆柱形永磁体下表面圆心为原点建立坐标系,如图2(a)所示.在圆柱中心轴线(z轴)上的点,由于对称性只受到z轴方向的磁场强度分量的作用,其他方向相互抵消.对z轴上的任意一点P的磁场强度H可以由z轴方向的磁场强度分量Hz表示[25]:其中(ρ,φ,z)为任意一点P点的柱坐标表示,z0为圆柱厚度,φ0为圆柱侧表面上从正z轴来看自x轴逆时针旋转到指定位置的角度.
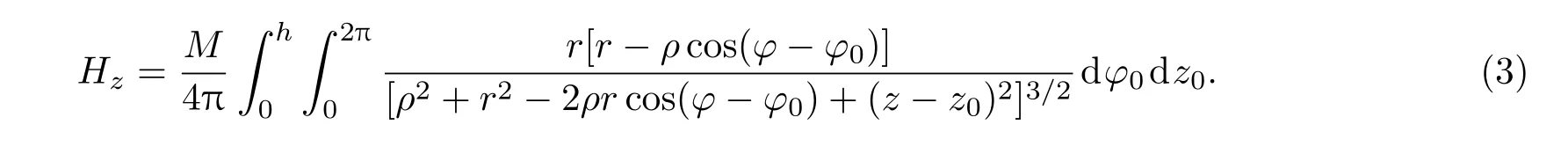
实验中,应用Matlab软件对磁场强度分量(3)式进行仿真分析,结果如图2(b)所示.由永磁体表面沿轴线远离,磁场强度逐渐减弱.
由于是均匀磁化,则B=H/µ0,µ0为真空磁导率其值为4π×10−7N/A2.由(2)和(3)式可得永磁体轴线上塞曼分裂与微位移之间的关系:
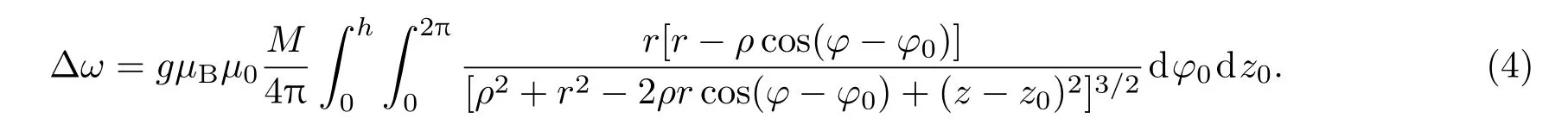
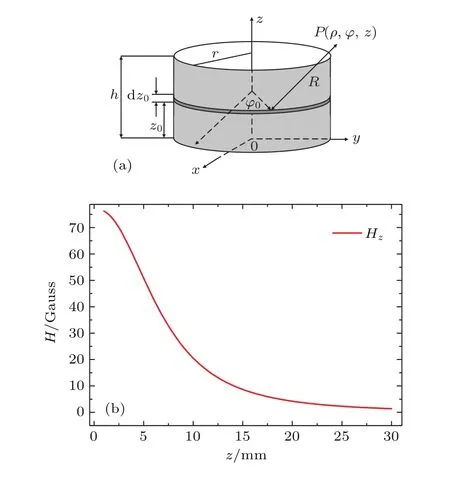
图2 (a)永磁体示意图;(b)z轴上的磁场强度仿真图Fig.2.(a)Schematic diagram of permanent magnet;(b)magnetic field intensity simulation graph on z axis.
2.2 微位移测量系统
测试系统示意图见图3,测试中信号源发出信号,并分成两路,其中一路信号进入微波源,对所发出的微波信号进行调制;另一路作为参考信号进入锁相放大器.微波源产生的微波信号通过微波天线作用在金刚石上,用于诱导金刚石NV色心的自旋翻转.激光器发出532 nm波长的激光,经过二向色镜(反射波长380—550 nm,透射波长584—700 nm)反射,并通过物镜将激光聚焦在金刚石上,使金刚石NV色心发生极化,并发出荧光.金刚石NV色心在微波和激光同时作用下,发出带有调制信息的ESR荧光信号,由物镜收集,透过二向色镜,经过平凸镜聚焦以及带通滤光片滤除550—750 nm波段以外的光,最后进入光电探测器采集.荧光信号分两路输出,一路直接用于观测ESR荧光信号;另一路通过锁相放大器得到对应的解调曲线.图中位移z方向为沿着永磁体轴线方向,且与金刚石[111]晶相同向.位移测试中通过高精度位移调节台实现金刚石与永磁体之间的距离调节,位移调节台的最小分辨率为0.01 mm.图中虚线框内区域处在磁屏蔽环境下.
本文在实验中应用到的金刚石样品采购于Element 6公司.该金刚石为典型的Ib型单晶金刚石,尺寸为4.5 mm×4.5 mm×0.5 mm,其抛光面为(100)晶面.
为了屏蔽地磁场以及周围环境磁场的干扰,实验均在由北京住信通光电技术有限公司生产的CPBT-W7型磁屏蔽系统内进行,其屏蔽剩磁优于0.1 nT.
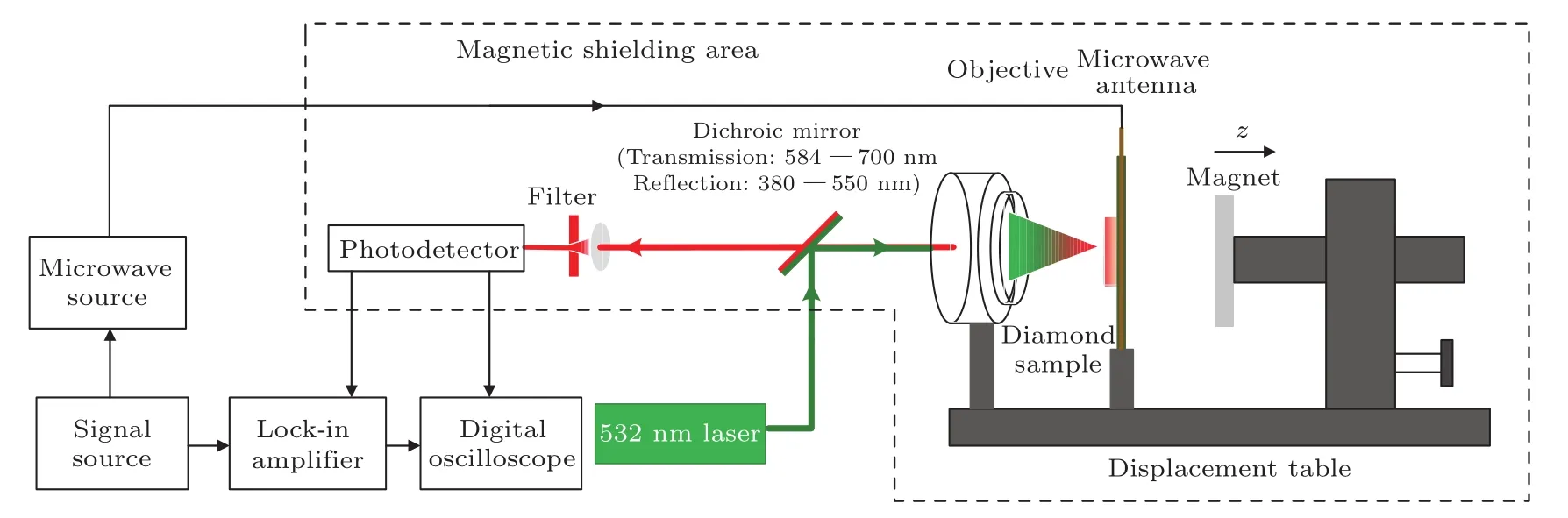
图3 测试系统示意图Fig.3.Schematic diagram of experimental setup.
3 测试与分析
3.1 永磁体磁梯度场测试
在进行位移测试前,应用青岛中宇环泰磁电科技有限公司生产的Model931型高斯计对永磁体磁场进行了测试.为了获得较大的磁场强度梯度,根据图2(b)的仿真结果,对沿永磁体轴线方向距离表面10 mm内的一段区域进行测试,并标定其线性程度.测试中,通过位移调节台将高斯计探头沿永磁体轴线移动,记录所在位置z与高斯计所测试的磁场强度H,测试结果如图4所示.

图4 实测沿z轴的磁场强度变化Fig.4.Magnetic field intensity along the z axis is measured.
通过直线拟合分析,可知在沿永磁体轴线方向4—7 mm范围内的磁场强度梯度为dH/dz=−7.77 Gauss/mm,线性相关系数为0.99725,所以可以将此范围磁场强度视为线性变化.沿轴线上某一位置z与磁场强度H的关系拟合直线方程为:
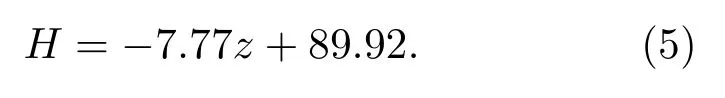
3.2 微位移测试与分析
为了建立塞曼分裂与位移之间的关系,将金刚石固定在高精度位移调节台上,并将永磁体固定在高精度位移调节平台的滑杆上.通过位移调节台调节永磁体到金刚石的距离,调节范围在测试磁场线性区域内,间隔0.1 mm记录位置z与对应的ESR荧光信号塞曼分裂频率,结果如图5(a)所示.通过直线拟合,得塞曼分裂与微位移的关联关系d(Δω)/dz=−21.67 MHz/mm,线性相关系数为0.99787,塞曼分裂频率随位置呈线性变化.
图5(b)为在测试磁场线性区内、位移间隔0.5 mm采集的ESR荧光光谱,图中横坐标为微波的扫频范围.根据(5)式可知,不同位置z所对应的磁场强度,图5(b)中的插图为对应位置的磁场强度与ESR塞曼分裂关系图.谱线由位置a到位置e随着磁感应强度逐渐减小,引起ESR的塞曼分裂频率减小,通过直线拟合得到的塞曼分裂频率与磁场强度之间关系d(Δω)/dH=2.79 MHz/Gauss.
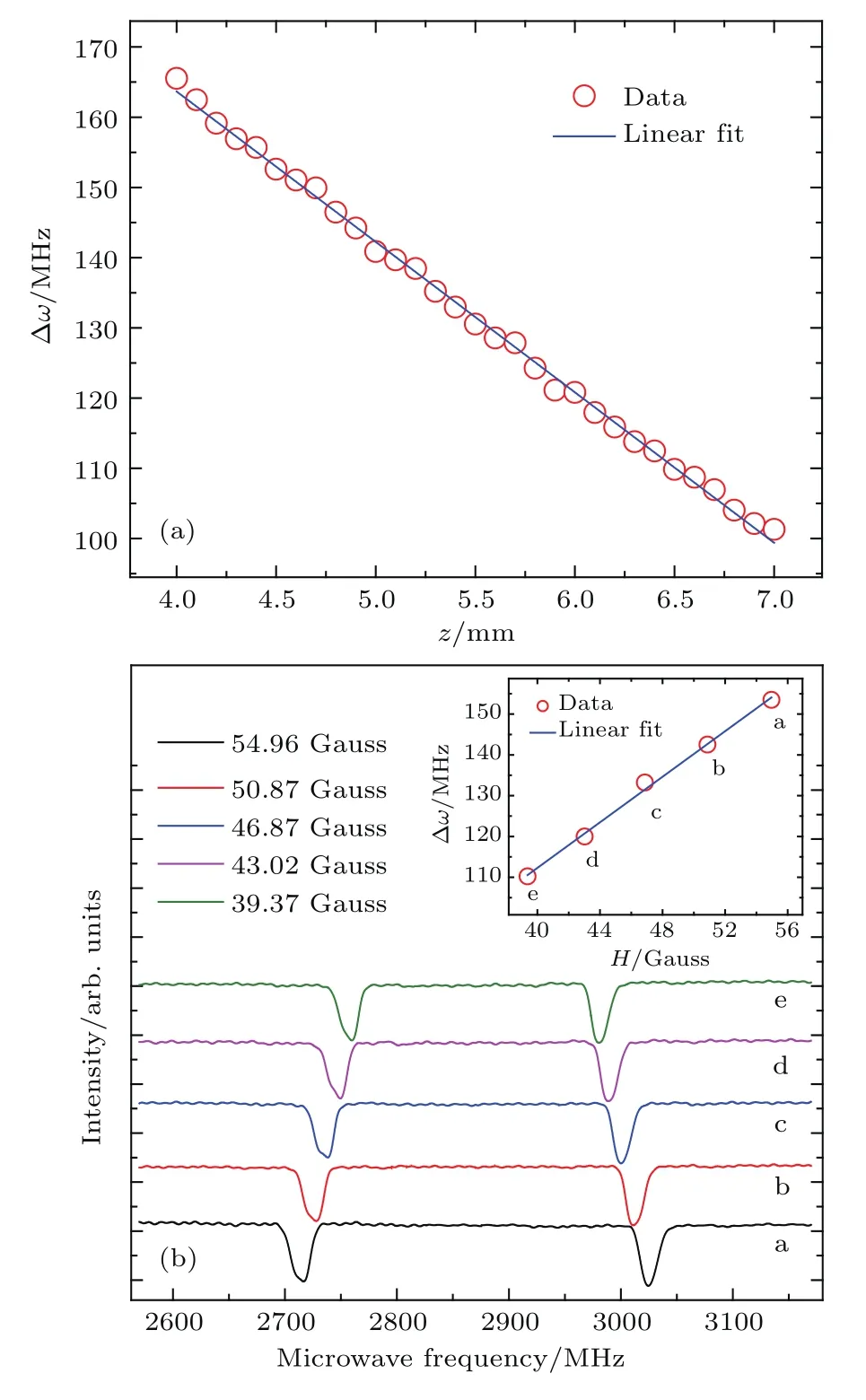
图5 (a)z轴上塞曼分裂频率随位置的变化;(b)不同磁场强度下ESR荧光光谱,插图为磁场强度与塞曼分裂频率关系的线性拟合,近似为2.79 MHz/GaussFig.5.(a)Zeeman splitting corresponding to various positions on z axis;(b)ESR fl uorescence spectra under different magnetic field intensity,the insert graph is the linear fi tting between Zeeman splitting and magnetic field intensity,the value is about 2.79 MHz/Gauss.
沿z轴正方向,在距离永磁体下表面5.5 mm(图5中位置c)处的磁场强度下,ESR荧光光谱标准化曲线的右侧共振谷如图6(a)中曲线a所示,共振频率fres=3000.56 MHz,曲线半高全宽FWHM=15.24 MHz,由塞曼分裂与微位移的关联关系d(Δω)/dz=−21.67 MHz/mm可得测试量程为0.70 mm.
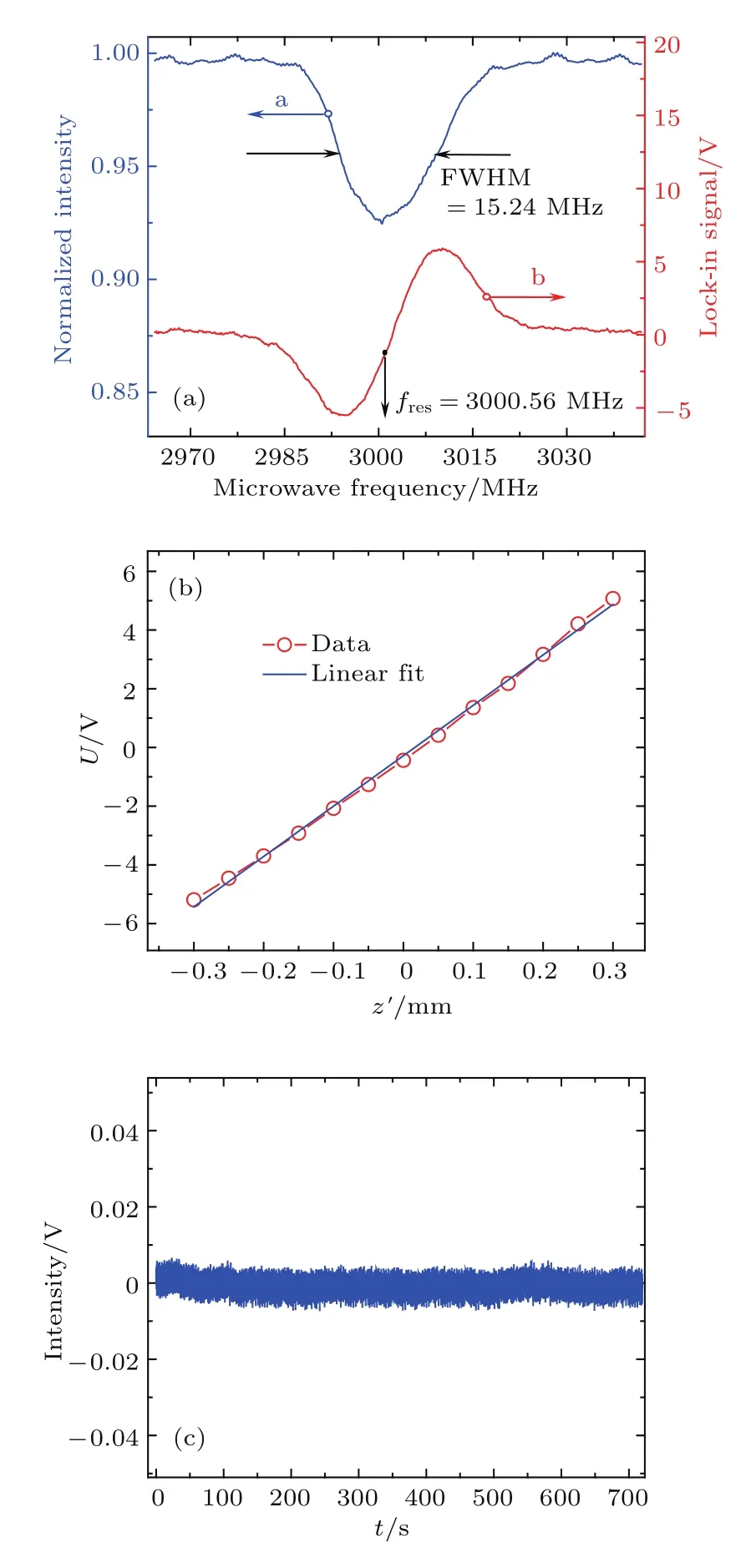
图6 (a)上侧曲线为ESR荧光信号右侧的共振谷,下侧曲线为锁相放大器输出曲线;(b)电压位移特性曲线;(c)系统输出噪声波形Fig.6. (a)Electron spin signal(curve a)and its corresponding lock-in ampli fier output(curve b);(b)relation between output voltage and displacement;(c)noise signal of system output.
通过外部信号源对微波信号施加调制频率25.8 kHz、调制幅值1.5 V的调制信号,同时通过锁相放大器对曲线a的荧光信号进行解调,得到的解调曲线如图6(a)中曲线b所示.由解调曲线b可以得出,在对应的荧光曲线半高全宽范围内,解调曲线的斜率α为0.74 V/MHz.根据斜率α的值,塞曼分裂频率随位置的变化可以通过电压上的变化表示,即U=αΔω(z).以图5中位置c作为位移传感测试的原点,用z′轴替代z轴,在±0.35 mm量程范围内进行测试.通过对系统位移调节,记录3000.56 MHz处对应锁相放大器输出信号的电压值,得到位移与电压之间的关系曲线如图6(b)所示.对其数据进行直线拟合,得到其灵敏度为16.67 V/mm,线性相关系数为0.99796.
在位移原点处,将微波源设置为3000.56 MHz定频输出,零位移量输入下,记录光电探测器输出的光强信号,通过去基线得到噪声波形,如图6(c)所示.对该噪声信号波形数据进行分析,计算得系统噪声的标准偏差为1 mV,由测试灵敏度可得位移测试系统分辨率为0.06µm.
本文利用金刚石NV色心塞曼分裂磁共振效应实现了对微位移的测量,测试系统的精度实现了60 nm的分辨,从实验中可以得到,该方法的测量精度由金刚石NV色心磁敏感测试分辨水平、磁体梯度场灵敏度以及电路系统对微弱电压信号的分辨水平决定.实验中采用了沿磁体轴向距离4—7 mm范围内进行微位移系统搭建与测试,磁梯度场为7.77 Gauss/mm,由磁体磁梯度场分布理论可知,距磁体表面越近,磁梯度场越大,因此,当微位移测量沿磁体轴向距离缩小到微米范围内,通过理论计算可以进一步提高微位移测量分辨率,有望能够达到亚纳米级水平.
4 结 论
本文利用电子自旋效应对磁梯度场的高精度敏感机理,结合磁梯度场与微位移之间的关系,研究了基于金刚石氮空位色心的电子自旋敏感磁机理的微位移测量方法.实验中首先通过建立电子自旋磁共振与微位移之间的关系,搭建了相应的微位移测量系统,该系统对微位移的测量灵敏度为16.67 V/mm,分辨率达到60 nm,并进一步分析该微位移测量方法的测量分辨率可达到更高量级.因此基于金刚石色心自旋磁共振效应的微位移测量方法在原子力显微系统、扫描探针系统等超精密扫描和控制技术领域有广泛的应用前景.该方法分辨率高,且系统简易、成本低,为超高分辨率微位移测量系统提供了新的研究思路.
[1]Dufrene Y F,Ando T,Garcia R,Alsteens D,Martinez-Martin D,Engel A,Gerber C Muller D J 2017Nat.Nanotechnol.12 295
[2]Marou fiM,Bazaei A,Moheimani S O R 2015IEEE T.Contr.Sys.T.23 504
[3]Swart I,Liljeroth P,Vanmaekelbergh D 2016Chem.Rev.116 11181
[4]Jiang C S,Repins I L,Beal C,Moutinho H R,Ramanathan K,Al-Jassim M M 2015Sol.Energ.Mat.Sol.C132 342
[5]Braunsmann C,Proksch R,Revenko I,Schaffer T E 2014Polymer55 219
[6]Voss A,Stark R W,Dietz C 2014Macromolecules47 5236
[7]An P,Guo H,Chen M,Zhao M M,Yang J T,Liu J,Xue C Y,Tang J 2014Acta Phys.Sin.63 237306(in Chinese)[安萍,郭浩,陈萌,赵苗苗,杨江涛,刘俊,薛晨阳,唐军2014物理学报63 237306]
[8]Parali L,Pechousek J,Sabikoglu L,Novak P,Navarik J,Vujtek M 2016Optik127 84
[9]Liu Y T,Li B J 2016Precis.Eng.46 118
[10]Peng Y X,Ito S,Shimizu Y,Azuma T,Gao W,Niwa E 2014Sensor Actuat.A:Phys.211 89
[11]Kronenberg N M,Liehm P,Steude A,Knipper J A,Borger J G,Scarcelli G,Franze K,Powis S J,Gather M C 2017Nat.Cell Biol.19 864
[12]Maletinsky P,Hong S,Grinolds M S,Hausmann B,Lukin M D,Walsworth R L,Loncar M,Yacoby A 2012Nat.Nanotechnol.7 320
[13]Mamin H J,Kim M,Sherwood M H,Rettner C T,Ohno K,Awschalom D D,Rugar D 2013Science339 557
[14]Cai J,Jelezko F,Plenio M B 2014Nat.Commun.5 4065
[15]Le S D,Pham L M,Bar G N,Belthangady C,Lukin M D,Yacoby A,Walsworth R L 2012Phys.Rev.B85 121202
[16]Clevenson H,Trusheim M E,Teale C,Schroder T,Braje D,Englund D 2015Nat.Phys.11 393
[17]Maertz B J,Wijnheijmer A P,Fuchs G D,Nowakowski M E,Awschalom D D 2010Appl.Phys.Lett.96 125
[18]Guo H,Chen Y L,Wu D J,Zhao R,Tang J,Ma Z M,Xue C Y,Zhang W D,Liu J 2017Opt.Lett.43 403
[19]Jensen K,Leefer N,Jarmola A,Dumeige Y,Acosta V M,Kehayias P,Patton B,Budker D 2014Phys.Rev.Lett.112 160802
[20]Liu D Q,Chang Y C,Liu G Q,Pan X Y 2013Acta Phys.Sin.62 164208(in Chinese)[刘东奇,常艳春,刘刚钦,潘新宇2013物理学报62 164208]
[21]Lai N D,Zheng D W,Jelezko F,Treussart F,Roch J F 2009Appl.Phys.Lett.95 191
[22]Balasubramanian G,Chan I Y,Kolesov R,Al-Homud M,Tisler J,Shin C,Kim C,Wojcik A,Hemmer P R,Krueger A,Hanke T,Leitenstorfer A,Bratschitsch R,Jelezko F,Wrachtrup J 2008Nature455 648
[23]Matsuzaki Y,Shimooka T,Tanaka H,Tokura Y,Semba K,Mizuoch N 2016Phys.Rev.A94 052330
[24]Ma J,Yang W M,Li J W,Wang M,Chen S L 2012Acta Phys.Sin.61 137401(in Chinese)[马俊,杨万民,李佳伟,王妙,陈森林2012物理学报61 137401]
[25]Wang R K,Zuo H F,Lü M 2011Aero.Compu.Tech.41 19(in Chinese)[王瑞凯,左洪福,吕萌 2011航空计算技术41 19]
