铟镓锌氧薄膜晶体管的悬浮栅效应研究∗

覃婷 黄生祥 廖聪维 于天宝 罗衡 刘胜 邓联文

(中南大学物理与电子学院,长沙 410083)

1 引 言

以有机矩阵发光二极管显示(active matrix organic light emitting diode,AMOLED)为代表的新型显示技术发展迅速,铟镓锌氧薄膜晶体管(InGaZnO thin fi lm transistor,IGZO TFT)有利于推动AMOLED等新型显示技术的大规模量产,成为下一代TFT技术的主流[1−3].研究者普遍认为,相比于传统的硅基TFT,IGZO TFT具有迁移率较高、均匀性好、成本低等优势[4−8].但是IGZO TFT的电学特性容易受到光照的影响,这可能成为影响AMOLED量产的一个重要技术问题.IGZO层的缺陷态电子可能受到光的激发而达到导带,从而导致器件泄漏电流的增加[9−12].

增加遮光层(light shielding layer)以减少光照对IGZO层的影响,是减少IGZO TFT的泄漏电流的主要方法[13].Lim等[14]和Takechi等[15]报道了增加遮光金属栅的IGZO TFT特性,证明了对遮光金属栅极施加合适的偏置电压能够较好地调控TFT的电学特性.此外,通过调制遮光金属栅的电压,还能够对IGZO TFT的阈值电压进行线性调节[16−19],这可能用于补偿AMOLED像素电路的阈值电压漂移.但是,在遮光金属栅上增加偏置电压或者电路,TFT的面积会增加,这也限制了高分辨率像素电路的集成[20].另一方面,Zan等[21]发现如果让遮光金属栅处于悬浮状态,可能提高器件的电学性能.但是,Zeng等[13]的实验表明,IGZO TFT的输出特性在遮光金属栅极悬浮情况下会呈严重的不饱和特性.这可能会严重影响到IGZO TFT在AMOLED像素及驱动电路中的应用.悬浮栅IGZO TFT的电学特性不能简单应用双栅极TFT[22]或单栅IGZO TFT[23]器件的机理来解释.然而迄今为止,悬浮栅IGZO TFT电学特性的机理解释尚未见报道.

本文采用TCAD(technology computer-aided design)研究了悬浮栅IGZO TFT中电势分布特点.根据IGZO TFT中电势的分布、输出电学特性推测了悬浮栅效应的产生机理,并建立了基于等效电容耦合方法的悬浮栅IGZO TFT输出特性模型.本文将TCAD数值模拟以及器件模型的结果与实验测量值进行了详细对比,较全面地揭示了悬浮栅效应的机制.

2 悬浮栅效应的TCAD分析

图1示意了具有遮光金属栅(shielding metal,SM)的IGZO TFT的器件剖面. 其中,x轴和y轴分别是沿着IGZO的沟道长度和厚度方向.IGZO TFT的W/L=25µm/10µm,IGZO层厚度tIGZO=40 nm,顶栅(top gate,TG,即遮光金属栅)和底栅(bottom gate,BG)介质层厚度均为200 nm.沟道长度L位于x轴15—25µm处,源极和漏极分别位于x轴0—15µm和25—40µm处,顶栅及底栅电极位于x轴0—40µm处.

在SILVACO TCAD分析中,有源层材料为IGZO,其缺陷态(defects)模型参数如表1所列.

图1 悬浮的和固定电位的遮光金属栅IGZO TFT的横截面示意图Fig.1.Cross sectional view of IGZO TFT with a fl oating/ fi xing SM.

表1 IGZO缺陷态密度模型参数Table 1.Density of states model parameters for IGZO.

图2分别是顶栅悬浮和顶栅接固定电位(VTG=0 V)时IGZO TFT的电势剖面图.如图2(b)所示,当遮光金属栅极接固定电位时,IGZO TFT的顶部与底部沟道的电势变化规律相同.即电势从源端到漏端逐渐增大,且电势的值在接近漏端附近陡增.并且电势的值在漏端处达到最大且保持不变.这是因为相比于IGZO沟道区,漏端附近的“夹断区”等效阻抗较大;于是漏源电压VDS主要降落在漏端附近的“夹断区”.漏端附近的电压陡增也说明漏端附近的“夹断区”内电场强度较大.此时,由于遮光金属栅极和主栅极的条件完全一致,故IGZO TFT的顶部和底部沟道的电势分布也是对称的.

图2(a)表明,IGZO TFT的悬浮栅及其介质层中的电势明显高于固定顶栅电位的电势.同时,顶部沟道与底部沟道的电势呈非对称变化.这可能是悬浮的遮光金属栅通过顶栅介质层与漏电极发生了电容耦合效应带来的.由于遮光金属栅电位的抬高,IGZO TFT在有源层顶部也形成了导电沟道,且IGZO层的顶部和底部导电沟道不对称,从而使得其电势分布也出现了显著的差异.

图2 (a)悬浮的,(b)固定电位的遮光金属栅IGZO TFT的电势分布剖面图(VDS=5 V)Fig.2.Potential distribution for IGZO TFT with(a)a fl oating SM and(b)a fi xing SM(VDS=5 V).

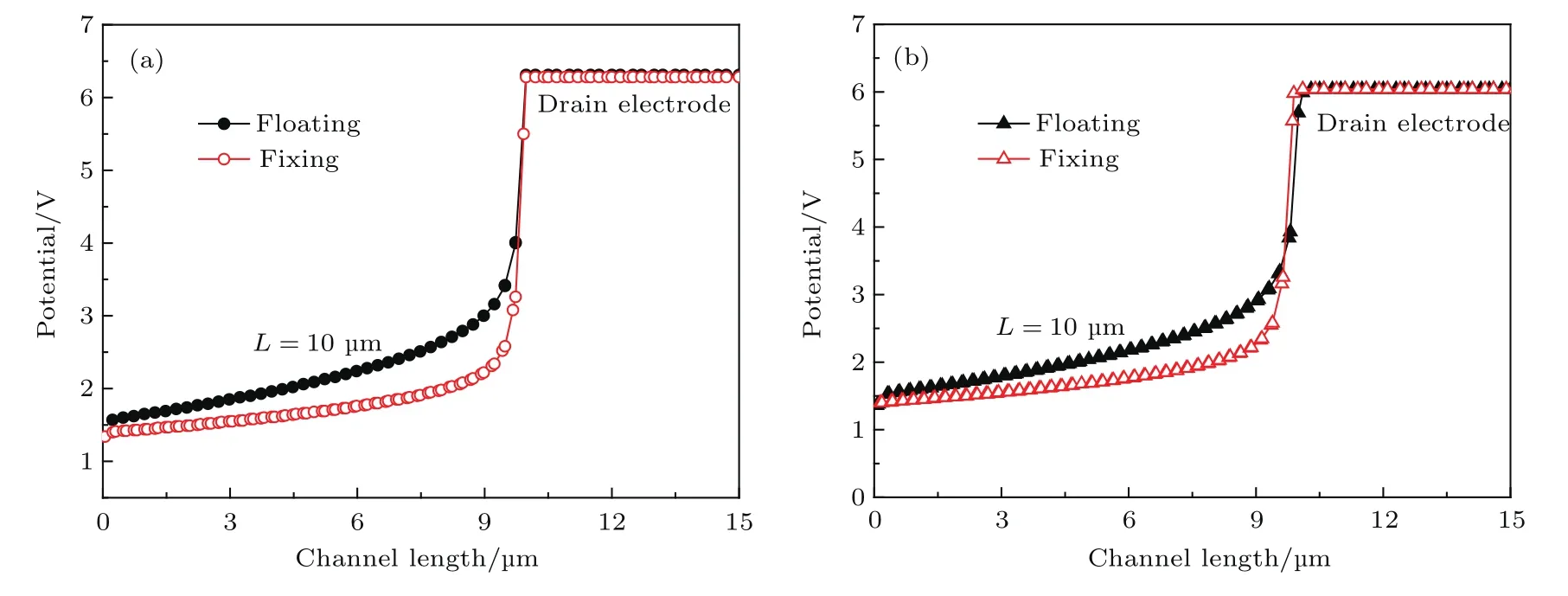
图3 IGZO层沟道电势变化曲线 (a)顶部沟道;(b)底部沟道Fig.3.Potential in the channel fi lm with(a)top channel(b)bottom channel.

图3示意了IGZO TFT的遮光金属层悬浮以及固定的状况下,IGZO的顶部沟道及底部沟道的电势值.相较于固定遮光金属栅的IGZO TFT,遮光金属栅悬浮的IGZO TFT的顶部沟道电势值在漏端附近提高了约1.5 V,底部沟道电势值也提高了约0.5 V.这是因为电容耦合作用,遮光金属栅极电压被提高.同时,悬浮栅效应增加了沟道中电场强度的x轴方向的分量,故IGZO顶部沟道以及底部沟道的电势均被抬高.又由于顶部沟道对电场强度的屏蔽作用,底部沟道电势的增加量比顶部沟道电势增加的量小一些.

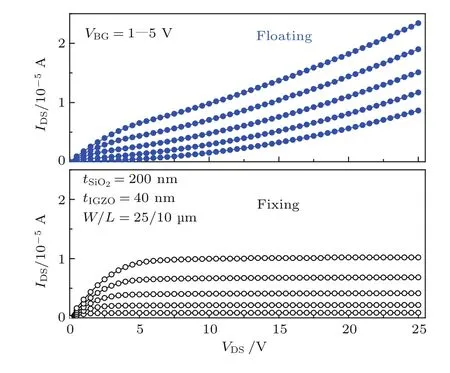
图4 遮光金属栅悬浮及接固定电位的IGZO TFT的输出特性曲线比较Fig.4.The output characteristics for IGZO TFT with a fl oating and fi xing SM.

也正是由于遮光金属栅悬浮时,IGZO TFT的沟道内电势与常规单栅器件存在显著的不同,器件的电学性能将相应地改变.图4示意了遮光金属栅悬浮和接固定电位时IGZO TFT的输出特性曲线.对于遮光金属栅接固定电位的器件而言,在器件的饱和区(VDS≥VGS−VTH),IDS的值趋于稳定且几乎不随VDS发生变化.但是遮光金属栅悬浮的IGZO TFT并不具备输出特性饱和特性,IDS的值在饱和条件(VDS≥VGS−VTH)下仍然不断地增加.我们称图4所示的现象为悬浮栅效应,即器件在满足饱和条件(VDS≥VGS−VTH)后电流仍然随着电压的增加而持续增加.

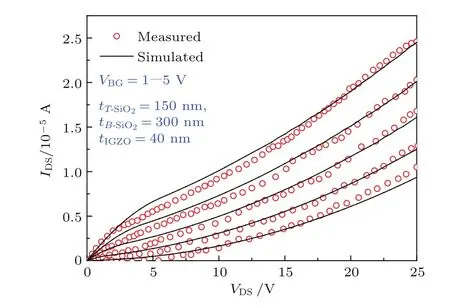
图5 悬浮遮光金属栅IGZO TFT的输出特性曲线的实验值与仿真值对比Fig.5.The output characteristics for IGZO TFT with a fl oating shielding metal for measured and simulated results by TCAD.

图5是遮光金属栅悬浮的IGZO TFT输出特性曲线测试值与TCAD数值分析结果的对比.TCAD数值分析的参数的设置与文献报道的工艺过程保持一致[13].其中,IGZO TFT的W/L=25/12µm,顶栅绝缘层(SiOx)厚度为150 nm,底栅绝缘层(SiOx)厚度为300 nm,IGZO层厚度为40 nm.图5表明,在遮光金属栅悬浮时,输出特性的不饱和现象显著.从图5的结果可看出,器件特性的测试值和TCAD计算值符合程度较高.但是,在VDS较小时,器件源漏电流的实验测试值相比于TCAD计算值低5%左右.这可能与测试过程的接触阻抗、TFT样品的参数分散性等相关.更长沟道的TFT的测试结果可能与TCAD数值分析结果复合程度更高.

3 悬浮栅效应模型

根据前面的推测,即悬浮栅效应由电容耦合引起,这里通过等效电容的方法建立悬浮栅IGZO TFT的电流模型.图6示意了遮光金属栅悬浮时IGZO TFT的等效电容分布.其中,tTI,tIGZO和tBI分别表示遮光金属栅绝缘层、IGZO层和底栅绝缘层的厚度.CTI与CBI分别表示单位面积的遮光金属栅与底栅绝缘层的电容.VFG,VBG分别是遮光金属栅(顶栅)和底栅上的电压.

事实上,遮光金属栅电极与源漏电极之间的耦合电场分布形状是非规则的.为了简化模型和计算,这里近似地采用平板电容来等效.后续将通过与数值计算的比较来检验该建模方法的准确性.

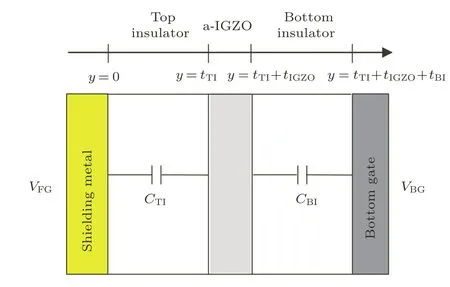
图6 遮光金属栅极悬浮的IGZO TFT的简化模型示意图Fig.6.Simpli fi ed cross-sectional view of IGZO TFT with a fl oating SM.

根据电容分压的原理,可以计算得到在遮光金属栅悬浮的情况下的悬浮栅电压VFG:

根据图2中悬浮遮光金属栅附近电势分布的特点,悬浮遮光栅极的电压会在IGZO层顶部形成新的导电沟道,并且同时会影响到IGZO层底部的电势分布,IGZO层底部的横向电场强度分量增强.从等效角度而言,悬浮遮光金属栅极的电压(VFG)使得IGZO层中的载流子浓度增加(CTIVFG).因此,阈值电压将在原底栅TFT的值的基础上近似地减小,可以表示为

其中,VBTH0仅存在底栅金属层时的IGZO TFT阈值电压.CDI=CBI+CTI.由此,悬浮遮光金属栅IGZO TFT的源漏电流[24]可以推导得到

其中,W,L,µ,VGS分别表示遮光金属层悬浮IGZO TFT沟道的宽度,沟道长度、有效迁移率和栅源电压.

当TFT器件工作于线性区时,即VDS≪VGS−VFTH,(3)式可以简化为

当VDS超过临界值(VGS−VFTH)时,源漏电流可以表示为

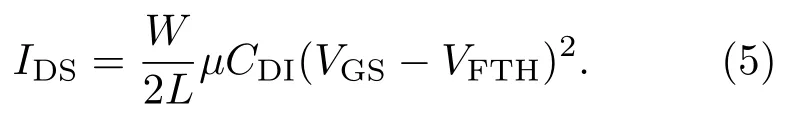
该模型表明,当VDS较小时,源漏电流与VGS仍然保持良好的线性关系;而VDS超过临界值以后,源漏电流与VGS变成二次函数关系.为了验证模型的合理性,图7示意了采用该模型的计算结果以及TCAD的数值计算结果.表2列出了模型的参数取值.

表2 模型参数的取值Table 2.Model parameters.

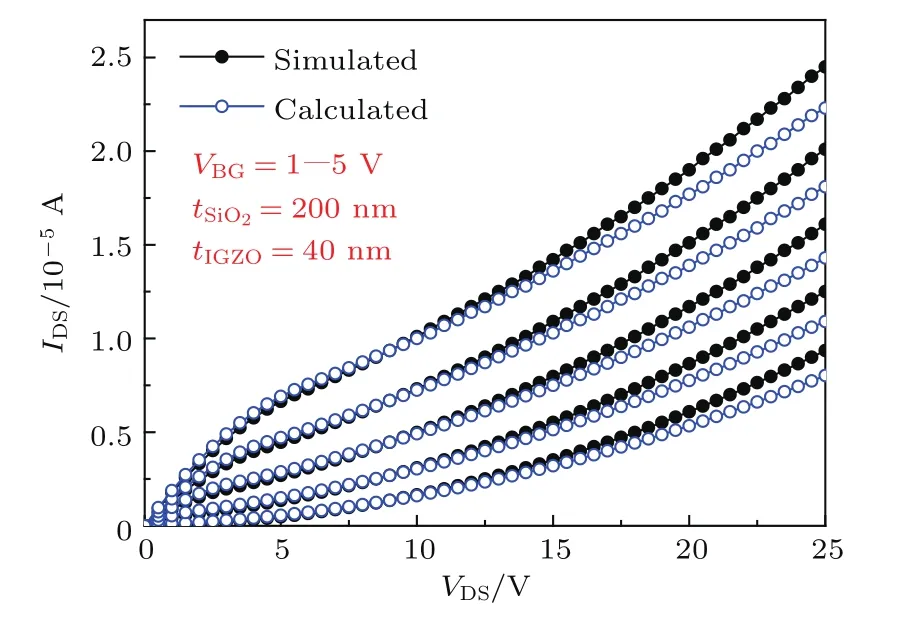
图7 遮光金属栅悬浮的IGZO TFT输出特性曲线,模型计算值与TCAD数值计算值的对比Fig.7.The comparison with calculated results and TCAD simulated results of output characteristics for IGZO TFT with a fl oating SM.

图7的对比表明,本文提出的电容耦合等效模型能够较准确地测算遮光金属栅悬浮时IGZO TFT的源漏电流特性.该模型的物理意义明显,表明了悬浮栅对阈值电压的调制作用,反映了悬浮栅控制下IGZO层新产生的导电沟道,能较准确地预计出器件输出特性由于VDS作用而不饱和的特点.

该模型采用等效电容的方法,将悬浮栅与源漏电极间的耦合电容近似认为是平板电容.但是这些电容值实际上并不是常数,而是受到源漏电压VDS的调制.另外,迁移率等参数同样受到栅源电压VGS的调制.这是造成图7所示解析模型计算结果与TCAD计算结果差异的根本原因.从图7来看,解析模型计算结果与TCAD计算结果的误差率小于10%,仍然具有较高的可信度.该模型具有数学结构简单、物理意义显著的优势,适合于手工计算.

图8 遮光金属栅悬浮的IGZO TFT输出特性曲线在不同λ的取值下的模型计算值对比Fig.8.The calculated output characteristics for IGZO TFT with a fl oating SM versus different value of λ.

根据以上分析可知,当电容耦合参数λ减少时,IGZO TFT的输出特性的饱和程度将被提升.图8表示了电容耦合参数λ取值不同时,悬浮栅IGZO TFT的输出特性曲线对比.当λ减小时,悬浮栅IGZO TFT的输出特性曲线“翘尾”程度降低.因此,当要求高输出阻抗的IGZO TFT时(例如,AMOLED的驱动TFT,或者用于TFT集成传感的放大器电路),主要手段应该是减少电容耦合参数λ.可能的方法包括,增加悬浮栅与IGZO TFT源极之间的电容、增加悬浮栅侧介质层厚度、在悬浮栅侧采用低介电常数的介质层等.

4 结 论

本文研究了遮光金属栅极悬浮的IGZO TFT的电学特性及悬浮栅效应的产生机制.通过TCAD数值计算,展示了悬浮栅IGZO TFT器件内的电势分布.分析表明,由于漏极电压对遮光金属栅极的耦合,IGZO层的电势和载流子浓度重新分配.在较强漏源电压VDS作用下,器件沟道方向的电场强度分量明显增强,IGZO层形成了顶部和底部两条非对称的导电沟道.本文建立了基于等效电容耦合的悬浮遮光金属栅IGZO TFT的漏源电流模型,该模型物理意义明显,且数学结构简单.本文的研究综合对比了悬浮遮光金属栅IGZO TFT的测试结果、TCAD数值计算结果以及模型计算结果,三者相互之间能够较好地符合,证实了所进行的TCAD数值计算以及所建立的器件物理模型的合理性.本文较全面地揭示了IGZO TFT悬浮栅效应的机制,对新型IGZO TFT的开发具有良好的指导作用.

[1]Arai T 2012J.Soc.Inf.Display20 156

[2]Li X F,Xin E L,Shi J F,Chen L L,Li C Y,Zhang J H 2013Acta Phys.Sin.62 108503(in Chinese)[李喜峰,信恩龙,石继锋,陈龙龙,李亚春,张建华2013物理学报62 108503]

[3]Xu P R,Qiang L,Yao R H 2015Acta Phys.Sin.64 137101(in Chinese)[徐飘荣,强蕾,姚若河2015物理学报64 137101]

[4]Kim Y,Kim Y,Lee H 2014J.Display Technol.10 80

[5]Qian C,Sun J,Zhang L,Huang H,Yang J,Gao Y 2015J.Phys.Chem.C119 14965

[6]Zhang C,Luo Q,Wu H,Li H,Lai J,Ji G,Yan L,Wang X,Zhang D,Lin J,Chen L,Yang J,Ma C 2017Organic Electron.45 190

[7]Zheng Z,Jiang J,Guo J,Sun J,Yang J 2016Organic Electron.33 311

[8]Liu F,Qian C,Sun J,Liu P,Huang Y,Gao Y,Yang J 2016Appl.Phys.A:Mater.Sci.Process.122 311

[9]Chen T C,Chang T C,Hsieh T Y,Tsai C T,Chen S C,Lin C S,Hung M C,Tu C H,Chang J J,Chen P L 2010Appl.Phys.Lett.97 192103

[10]Oh H,Yoon S M,Ryu M K,Hwang C S,Yang S,Park S H K 2010Appl.Phys.Lett.97 183502

[11]Oh H,Yoon S M,Ryu M K,Hwang C S,Yang S,Park S H K 2011Appl.Phys.Lett.98 033504

[12]Chen W T,Hsueh H W,Zan H W,Tsai C C 2011Electrochem.Solid-State Lett.14 H297

[13]Zeng M,Chen S,Liu X D,Zeng L M,Li W Y,Shi L Q,Li S,Chou Y F,Liu X,Lee C 2017Sid Symposium Digest of Technical Papers48 1234

[14]Lim H,Yin H,Park J S,Song I,Kim C,Park J,Kim S,Kim S W,Lee C B,Kim Y C,Park Y S,Kang D 2008Appl.Phys.Lett.93 063505

[15]Takechi K,Nakata M,Azuma K,Yamaguchi H,Kaneko S 2009IEEE Trans.Electron Dev.56 2027

[16]Park J S,Jeong J K,Mo Y G,Kim H D,Kim C J 2008Appl.Phys.Lett.93 033513

[17]Seok M J,Choi M H,Mativenga M,Geng D,Kim D Y,Jang J 2011IEEE Electron Dev.Lett.32 1089

[18]Abe K,Takahashi K,Sato A 2012IEEE Trans.Electron Devi.59 1928

[19]Baek G,Kanicki J 2012J.Soc.Inf.Disp.20 237

[20]Seok M J,Mativenga M,Geng D,Jang J 2013IEEE Electron Dev.Lett.60 3787

[21]Zan H W,Chen W T,Yeh C C,Hsueh H W,Tsai C C,Meng H F 2011Appl.Phys.Lett.98 153506

[22]Qin T,Huang S X,Liao C W,Yu T B,Deng L W 2017Acta Phys.Sin.66 097101

[23]Ning H L,Hu S B,Zhu F,Yao R H,Xu M,Zou J H,Tao H,Xu R X,Xu H,Wang L,Lan L F,Peng J B 2015Acta Phys.Sin.64 126103(in Chinese)[宁洪龙,胡诗犇,朱峰,姚日晖,徐苗,邹建华,陶洪,徐瑞霞,徐华,王磊,兰林锋,彭俊虎2015物理学报64 126103]

[24]Zhao J Q,Yu P F,Qiu S,Zhao Q H,Feng L R,Ogier S,Tang W,Fan J L,Liu W J,Liu Y P,Guo X J 2017IEEE Electron Dev.Lett.64 2030