三维漏斗中颗粒物质堵塞问题的数值实验研究∗

麻礼东杨光辉张晟林平田园杨磊

1)(中国科学院近代物理研究所,兰州 730000)

2)(中国科学院大学物理学院,北京 100049)

3)(兰州大学信息科学与工程学院,兰州 730000)

1 引 言

颗粒物质是由众多离散颗粒相互作用而形成的具有内在有机联系的复杂系统.自然界中单个颗粒的典型尺度在10−6—10 m范围内,其运动规律服从牛顿定律;整个颗粒介质在外力或内部应力状况变化时发生流动,表现出流体的性质,从而构成颗粒流.颗粒物质看似非常简单(相互作用通常只有摩擦、碰撞和重力),但随着研究的不断深入,人们开始发现颗粒物质表现出的动力学行为其实异常复杂[1−3],传统的流体动力学理论和热力学理论均不能完整地用于描述颗粒介质的流动行为,其中一个典型的挑战就是如何描述颗粒物质的堵塞现象.

近年来,颗粒物质的堵塞行为是物理学和工程领域研究中的一个热点和难点问题[4−6].颗粒体系的堵塞构形、密度变化以及颗粒物质从容器开口流出时的堵塞行为和临界特征等,都得到广泛而深入的研究和普遍关注.事实上,堵塞现象在很多系统都可以发生[7],如悬浮微粒通过狭窄通道,液氦表面电子通过纳米通道,第二类超导中的旋涡结构以及人或动物通过窄门等.这些系统的堵塞行为本质上与颗粒系统类似,但是至今还没有明确的解释.对于颗粒系统,当开口尺寸与颗粒的大小相差不大时,在开口的上方很容易形成稳定的拱结构,从而阻碍了颗粒的流动,导致堵塞的发生.

在各种颗粒流动的研究中,重力驱动下的漏斗流中的堵塞现象研究得最为深入,关于堵塞的解释已有了许多理论模型[8,9],同时对于二维漏斗是否存在一个堵塞的临界开口尺寸是一个有争议的问题[9−11].在实验中为了得到尽可能多的堵塞事例,在堵塞形成后,通常会采取振动或喷入气流的方法破坏拱结构,使得流动重新开始,直到下一次稳定的拱结构的出现.Kondic[12]对于二维锥形漏斗的模拟显示,从流动开始到堵塞的时间t的概率分布P(t)随t呈e指数下降的趋势.Guariguata等[13]构建了水平放置的、由水流驱动的颗粒堵塞研究平台,结果发现水流流速对于堵塞概率的影响很小.Lin和Fang[14]研究了椭圆颗粒流中的堵塞问题,发现椭圆的长轴短轴之比对于堵塞概率有着明显的影响.Longjas等[15]的研究发现漏斗中颗粒粒径不均一性会使得破坏拱结构变得困难.Kunte等[16]对于多个开口的漏斗流中的堵塞问题进行了研究,发现堵塞概率明显小于只有一个开口时的情况.Hong等[17]利用油滴做实验的结果暗示了当摩擦趋于零时堵塞概率也将趋于无穷小.

Zuriguel等[4,18−22]做了一系列实验,研究了颗粒物质从三维圆筒中流出的堵塞行为,他们得到了数千个堵塞的事例,测量了连续两次堵塞之间的坍塌规模s(两次堵塞之间从开口流出的颗粒数目).实验发现:1)颗粒材料特性以及表面粗糙度对坍塌规模几乎没有影响,但颗粒形状对坍塌规模有显著影响;2)平均坍塌规模〈s〉和R−Rc的倒数成幂律关系,其中R为开口尺寸,Rc为临界开口尺寸;3)临界堵塞半径随形状改变而变化,但临界指数几乎不变化;4)在开口上方放置障碍物可以明显地减小堵塞的概率.Saraf和Franklin[23]用三维不对称锥形漏斗做堵塞实验,发现不同于Zuriguel等的结论,崩塌概率P(s)和崩塌规模s之间呈幂律关系.在以上实验过程中,为了触发下一次坍塌,他们用压缩气体来冲击开口附近行成的拱结构.然而气体冲击对实验结果的影响有多大并没有进行评估.为此,本文采用数值模拟的方法,研究当漏斗开口打开后的第一次堵塞行为,避免了实验上为触发下一次坍塌而引入的干扰,并讨论了漏斗开口尺寸、漏斗锥角等对坍塌规模的影响.

2 数值模拟模型

目前,对于颗粒体运动的数值分析方法主要分为:连续介质方法和离散元方法.本文利用自主开发的、基于离散元方法和分子动力学的多GPU(graphics processing unit)并行程序[24,25].模拟中采用Hertz-Mindlin非线性接触模型计算颗粒间的作用力,对于两个相互接触的球形颗粒i和j(半径分别为Ri和Rj;位矢为ri和rj;速度为vi和vj;角速度为ωi和ωj),它们之间的作用力由法向力Fnij和切向力Ftij构成.在法线方向上,颗粒间作用力包括Hertz弹性力和阻尼力,即

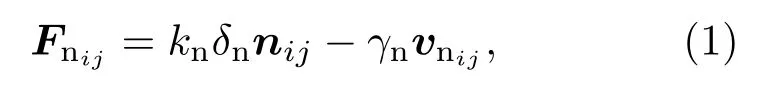
式中,δn=Ri+Rj−rij(其中rij=ri−rj,rij=|rij|)为颗粒间的法向重叠量;nij=rij/rij为颗粒间的法向单位向量;vnij=(vij·nij)nij(其中vij=vi−vj)为颗粒间的法向相对速度;

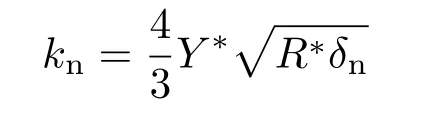
和

分别是法向弹性系数和法向阻尼系数,其中等效弹性模量Y∗,等效半径R∗以及等效质量m∗分别由公式

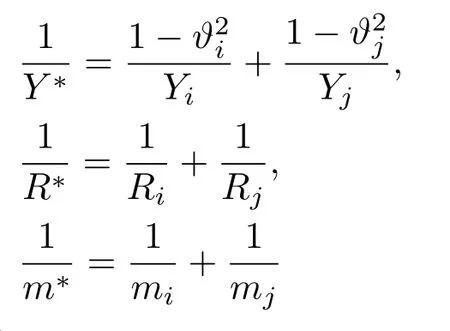
决定;e为颗粒间碰撞的恢复系数;ϑ为泊松比.在切向上,基于Mindlin理论,颗粒间的切向力可表述为

式中

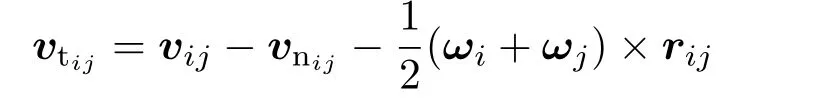
为颗粒间的切向相对速度;utij为颗粒间的切向位移,它与颗粒的接触时间有关,刚接触时它的值为0(即utij|t=0),随后其值由公式

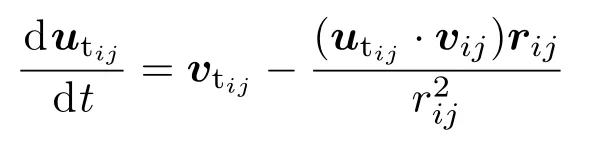
(此公式的第二项来源于刚体在接触点的转动,确保切向位移utij总是与接触平面垂直)决定;和

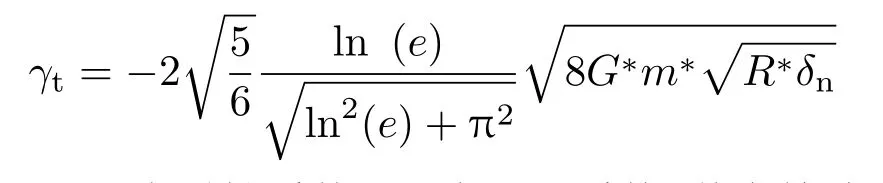
分别是切向弹性系数和切向阻尼系数,其中等效切向模量G∗由公式

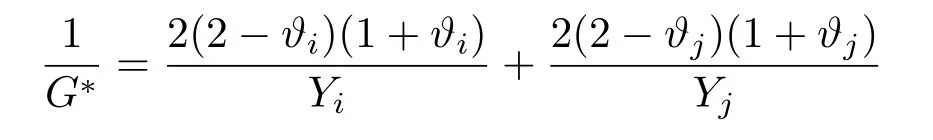
决定.此外,通过截断切向位移utij的大小来确保Mohr-Coulomb屈服条件(即|Ftij|≤|µFnij|,µ为颗粒间的摩擦系数).如果颗粒与刚性边界接触,则可将边界设为半径无限大的球体.然后在重力的作用下,球形颗粒i的运动方程可写为

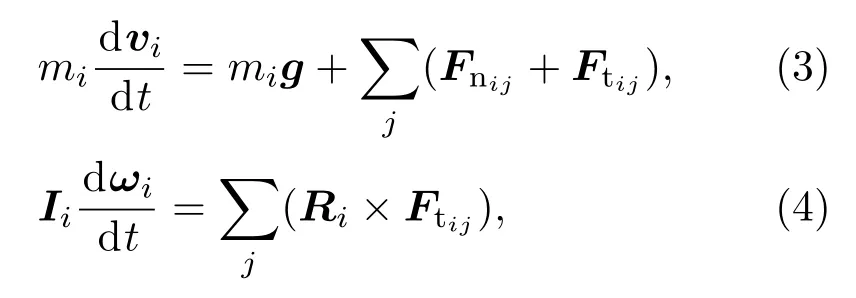
其中mi,vi,Ii,ωi分别为颗粒i的质量、速度、转动惯量和角速度;Ri是从颗粒的中心指向接触点的向量,它的模就是颗粒的半径.

图1所示为本文所用的模型.模拟过程中只考虑颗粒所受的重力、颗粒之间及颗粒与漏斗之间的摩擦力和碰撞力,不考虑空气阻力.重力方向沿漏斗轴向竖直向下.初始时刻起,5000个颗粒随机从一个固定水平面产生,然后在重力的作用下落入漏斗中.一段时间后,颗粒在漏斗中处于稳定静止堆积状态,去除漏斗出口的挡板后,颗粒在重力作用下开始运动.然后统计从去除挡板到第一次堵塞之间流出的颗粒数目,整个过程模拟1.2×107个时间步长(即6 s,其中堆积用时1 s,时间步长见表1).为了使模拟结果具有统计学意义,对于每个固定的漏斗开口尺寸和漏斗锥角,重复10000次模拟,而且每次模拟中用到的初始堆积构型都不一样(在模拟过程中通过改变颗粒初始产生速度获得).对于5000个颗粒构成的系统,使用一块GPU模拟是足够的,且计算采用双精度浮点数,一个时间步长将耗费约0.1 ms计算时间,因此一个模拟过程将花费约20 min.模型中的参数取值见表1.

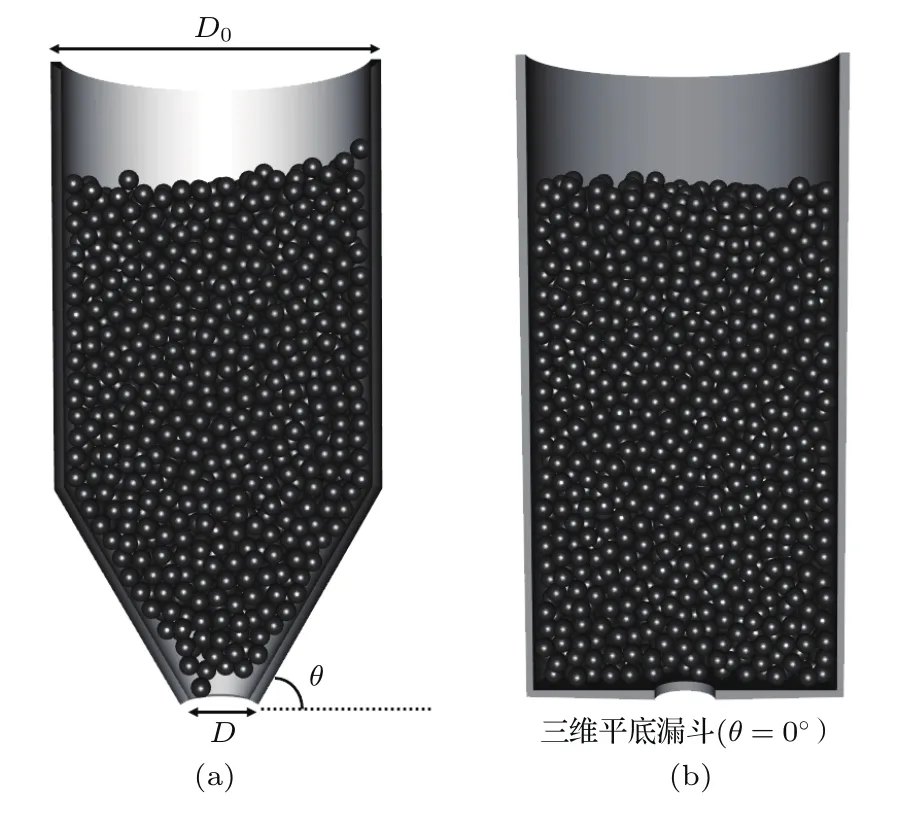
图1 数值模型 (a)三维锥形漏斗;(b)三维平底漏斗(θ=0°)Fig.1.The simulation models:(a)Three-dimensional conical hopper;(b)three-dimensional fl at hopper(θ =0°).

表1 颗粒、漏斗的模拟参数Table 1.Simulation parameters of grains and hopper.

3 结果分析与讨论

3.1 坍塌规模的概率分布

根据从去除挡板到第一次堵塞之间流出的颗粒数,统计得到平底漏斗(θ=0°)当开口D=3d时在10000次模拟中的坍塌规模,统计结果(坍塌规模的概率分布)如图2所示,横坐标为坍塌规模(流出的颗粒数),纵坐标为坍塌规模出现的概率.从图2中可以看出,坍塌规模大于40的概率非常小.而且在坍塌规模等于6时,概率分布出现了1个峰值.峰值的左边数据似乎为幂函数增长(图3中的插图),但由于数据点太少,这个现象还没有得到很好的理解,在Zuriguel等[18]的实验中,气体冲击的持续时间、气压以及漏斗尺寸对它都有影响.

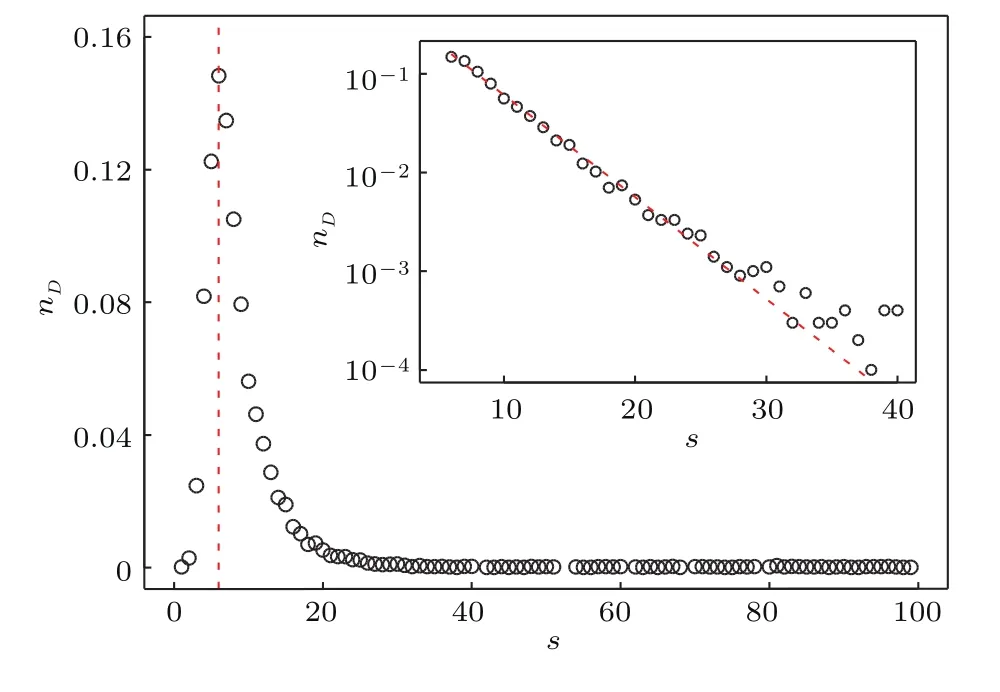
图2 坍塌规模的概率分布(平底漏斗开口D=3d)Fig.2.Probability distribution of collapse scale(hopper outlet D=3d).

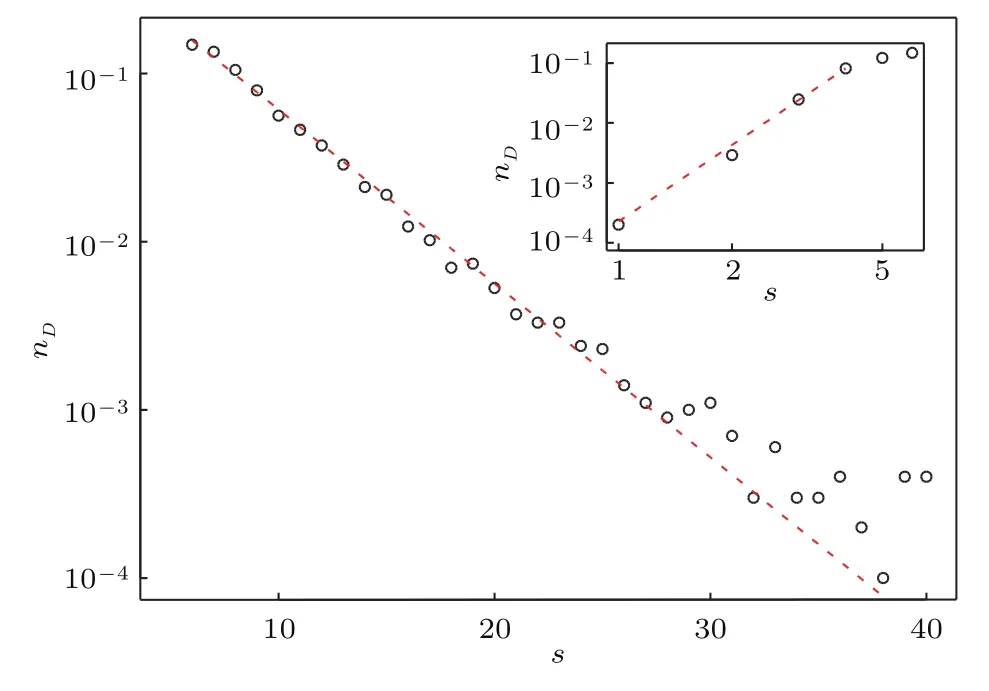
图3 坍塌规模的概率分布(平底漏斗开口D=3d,主图表示峰值右边概率分布(半对数图);插图表示峰值左边概率分布(双对数图))Fig.3.Probability distribution of collapse scale(hopper outlet D=3d;main fi gure,log plot of probability on the right of the peak in Fig.2;inset,log-log plot of probability on the left of the peak in Fig.2).

峰值右边的概率分布呈指数衰减形式(图3主图),意味着存在一个特征参数控制这个系统.为此图4显示了所有开口尺寸下归一化坍塌规模(s/〈s〉)的概率分布.从图中可以看出,所有概率分布曲线基本上塌缩到一条单一曲线.由于峰值左边的分布呈幂函数(不是指数形式),所以这部分没有很好地塌缩至单一曲线.但是峰值右边几乎可以坍缩至相同斜率的曲线.峰值右边数据呈指数衰减可以用如下简单概率模型[11]解释:假定每个颗粒从开口流出的概率为p,并与其他颗粒无关(独立事件),那么一个颗粒发生堵塞的概率为(1−p),则坍塌规模为s的概率为有趣的是,坍塌规模的概率分布与颗粒间的相互作用力[26]非常相似,在某种程度上表明,颗粒的堵塞行为与颗粒介观结构(颗粒间的力链和力网)的静力学稳定性密切有关.

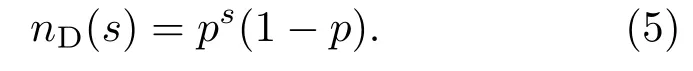
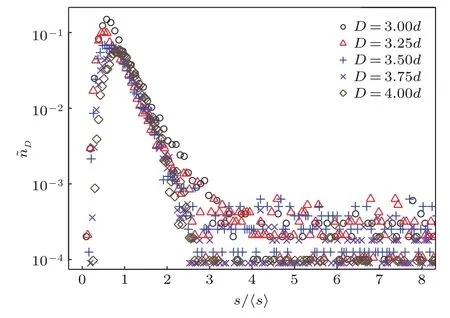
图4 坍塌规模的概率分布(不同平底漏斗开口尺寸,半对数图)Fig.4.Probability distribution of collapse scale(with various hopper outlet size,log plot).

3.2 临界开口尺寸

值得特别注意的一个问题是:漏斗流中是否存在一个临界开口尺寸Dc,当开口尺寸大于临界尺寸时不会出现堵塞现象?直观上,这个问题很难回答.从原理上来说,即使当漏斗开口尺寸很大时,还是可能形成非常大的拱结构进而发生堵塞现象,只是这种情况下一般要等待足够长的时间才能观察到.为此,图5显示了在平底漏斗中,平均堵塞规模〈s〉与漏斗开口尺寸D之间的变化规律.从图中可以看出,随着开口尺寸的增加,平均堵塞规模开始发散.为了说明这是一个相变(低于临界开口尺寸,会出现堵塞现象;高于临界开口尺寸,不会出现堵塞现象),需要观察平均堵塞规模〈s〉在临界开口附近是否满足幂函数分布.由于不清楚确切的临界开口尺寸的大小,模拟上会比较困难.不过,参考文献[18],利用用如下幂函数去拟合数据:

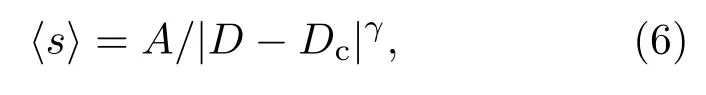
其中A和γ是常数.拟合结果显示在图5中,其中A=123.8,Dc=4.75,γ=1.5.通过拟合,在本文的系统中,临界开口尺寸在4.75d左右.

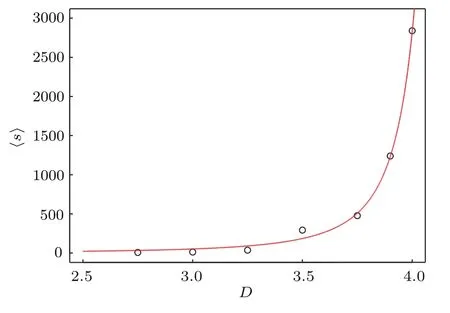
图5 平底漏斗中平均坍塌规模〈s〉与开口尺寸D的关系Fig.5.Relation of averaged collapse scale 〈s〉and hopper outlet size.

3.3 漏斗锥角的影响

进一步地,研究了漏斗锥角θ对于堵塞问题的影响,其中漏斗直径(D0=15d)以及漏斗开口尺寸(D=3d)都固定不变.研究发现当θ为15°时(图6),坍塌规模的分布和平底漏斗(即θ=0°)区别不大,而当θ大于45°时,坍塌规模的分布为两个峰,一个集中在s＜3的区域,另一个峰值大约在s=9,这个峰值略大于平底漏斗时s的峰值(s=6).关于第一个峰值的存在很容易理解,锥形漏斗开口容易使得在堆积过程中开口附近就形成比较稳定的拱结构,从而使得体系未经流动而直接进入了堵塞的状态.而从s＞10的概率分布来看,漏斗锥角的增大会使得s＞10的事件出现的频率变高.

同样地,在漏斗流中是否存在一个临界漏斗锥角θ,当锥角大于临界值时堵塞不会发生.考虑到当漏斗锥角接近临界值时坍塌规模将非常大,为此我们模拟了一个颗粒体系更大的漏斗流(颗粒数为40000).研究结果发现,当θ≥77°时,系统几乎不会堵塞(坍塌规模大于40000).显而易见的是,当θ=90°时(即漏斗变成一根直管),不应该发生堵塞,我们的数值结果表明在三维漏斗中这个临界值大约为77°.这个临界值和文献[8]中提到的二维漏斗中的临界角度75°很接近.

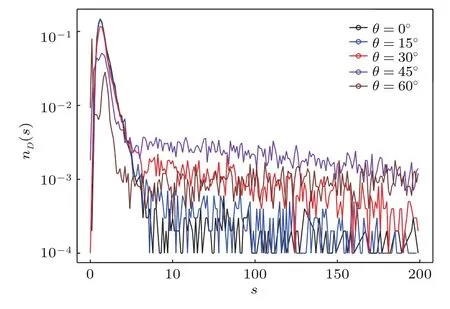
图6 不同漏斗锥角θ(漏斗开口D=3d)时,坍塌规模的概率分布Fig.6.Probability distribution of collapse scale with various hopper angle(hopper outlet D=3d).

4 结 论

利用自主开发的GPU程序,我们通过建立三维漏斗流颗粒模型,模拟了颗粒通过圆形开口过程中颗粒堵塞现象,研究了坍塌规模与开口尺寸之间的关系,临界开口尺寸是否存在,漏斗锥角对于堵塞概率影响等问题.得到如下结论:

1)对于固定的漏斗开口尺寸,坍塌规模概率分布在峰值右边满足指数衰减分布;

2)通过归一化,发现所有开口尺寸的峰值右边的坍塌规模分布可以基本上坍缩到单一曲线上;

3)坍塌规模概率分布在峰值右边呈指数分布的现象,可以用一个简单的概率模型进行解释;

4)通过拟合平均坍塌规模与开口尺寸之间的关系,发现存在一个临界开口尺寸,当开口尺寸大于这个临界尺寸时,堵塞将不再发生;

5)当漏斗锥角θ≤60°时,θ对于平均坍塌规模影响不大,但存在一个临界角度,当θ超过这个临界角度后系统将不再发生堵塞.

[1]Peng Y J,Zhang Z,Wang Y,et al. 2012Acta Phys.Sin.61 134501(in Chinese)[彭亚晶,张卓,王勇,等2012物理学报61 134501]

[2]Xie X M,Jiang Y M,Wang H Y,et al. 2003Acta Phys.Sin.52 2194(in Chinese)[谢晓明,蒋亦民,王焕友,等2003物理学报52 2194]

[3]Lu K Q,Hou M Y,Jiang Z H,et al. 2012Acta Phys.Sin.61 119103(in Chinese)[陆坤权,厚美瑛,姜泽辉,等2012物理学报61 119103]

[4]Zuriguel I,Pugnaloni L A,Garcimartin A,Maza D 2003Phys.Rev.E68 3

[5]Thomas C C,Durian D J 2015Phys.Rev.Lett.114 17

[6]Lu K,Liu J 2004Physics33 10(in Chinese)[陆坤权,刘寄星2004物理33 10]

[7]Zuriguel I,Parisi D R,Hidalgo R C,Lozano C,Janda A,Gago P A,Peralta J P,Ferrer L M,Pugnaloni L A,Clement E,Maza D,Pagonabarraga I,Garcimartin A 2014Sci.Reports4 7324

[8]To K,Lai P Y,Pak H K 2001Phys.Rev.Lett.86 1

[9]Masuda T,Nishinari K,Schadschneider A 2014Phys.Rev.Lett.112 13

[10]To K W 2005Phys.Rev.E71 6

[11]Janda A,Zuriguel I,Garcimartin A,Pugnaloni L A,Maza D 2008EPL84 4

[12]Kondic L 2014Granular Matter16 2

[13]Guariguata A,Pascall M A,Gilmer M W,Sum A K,Sloan E D,Koh C A,Wu D T 2012Phys.Rev.E86 6

[14]Lin Y J,Fang C 2016J.Mech.32 6

[15]Longjas A,Monterola C,Saloma C 2009J.Statist.Mech.Theory and Experiment2009 05006

[16]Kunte A,Doshi P,Orpe A V 2014Phys.Rev.E90 2

[17]Hong X,Kohne M,Weeks E R 2015arXivpreprint

[18]Zuriguel I,Garcimartin A,Maza D 2005Phys.Rev.E71 5

[19]Mankoc C,Garcimartin A,Zuriguel I,Maza D 2009Phys.Rev.E80 1

[20]Zuriguel I 2014Papers in Physics6 060014

[21]Zuriguel I,Janda A,Garcimartin A,Lozano C,Arevalo R,Maza D 2011Phys.Rev.Lett.107 27

[22]Lozano C,Janda A,Garcimartin A,Maza D,Zuriguel I 2012Phys.Rev.E86 3

[23]Saraf S,Franklin S V 2011Phys.Rev.E83 3

[24]Tian Y,Qi J,Lai J,Zhou Q,Yang L 2013Proceedings of the Awareness Science and Technology and Ubi-Media ComputingAizu-Wakamatsu,Japan,November 2–4,2013 p547

[25]Tian Y,Zhang S,Lin P,Yang Q,Yang G,Yang L 2017Comput.Chem.Engineer.104 231

[26]Snoeijer J H,van Hecke M,Somfai E,van Saarloos W 2003Phys.Rev.E67 3