线性不可逆热力学框架下一个无限尺寸热源而有限尺寸冷源的制冷机的性能分析∗

2018-03-26张荣卢灿灿李倩文刘伟白龙

物理学报 2018年4期

张荣卢灿灿李倩文刘伟白龙

(中国矿业大学物理科学与技术学院,徐州 221116)

1 引言

当前,能源的存储和利用已经成为全世界所面临的一个重要问题.由于不可再生能源的日益枯竭(例如:石油,煤炭,天然气等),有效利用不可再生和可再生能源已经成为节约能源和维持社会可持续发展的重要途径之一.热机作为一种将热能转换为机械能的装置,自发明以来一直在人们的工农业生产和生活中发挥着重要作用.值得注意的是,热机(包括制冷机)的效率η(制冷系数ε)会受到卡诺定理的限制,即η≤ηC=1−Tc/Th[ε≤εC=Tc/(Th−Tc)],这里Th和Tc分别是高低温热源的温度,ηC和εC分别是卡诺效率和卡诺制冷系数.然而,由于卡诺热机(制冷机)的工作过程是准静态过程,导致其输出(输入)功率为零,这使得基于卡诺循环的热设备的使用受到了极大制约.20世纪50—70年代,Yvon,Chambadal,Novikov,Curzon和Ahlborn等研究了工质与高低温热源接触满足有限时间的热转移过程[1,2],并给出了有限时间条件下的热机在最大功率时的效率,即所谓CA效率他们的先驱性工作标志着有限时间热力学的诞生.随后,有限时间热力学与线性不可逆热力学的等价性被证明[3],这进一步丰富了有限时间热力学的科学内涵.目前,有限时间热力学因其理论的实用性已经成为热力学研究的一个活跃领域[4−12].

众所周知,人们对于热机(制冷机)的研究通常是假设热源的尺寸无限大(或者高低温热源的温度保持不变)的条件下进行的.而事实上,这种理想化的条件使得对于热机(制冷机)的性能优化缺乏一定的工程实用性.基于有限时间热力学方法,一些研究表明高低温热源的尺寸对于热机性能有着重要影响[13−16].高低温热源均为有限尺寸情况下的热机研究给出了一个内可逆循环热机性能的优化关系[17].基于线性不可逆热力学方法,高温热源尺寸有限而冷源尺寸无限情况下的研究表明:在紧耦合条件下热机的最大输出功为有效能的一半,相应的效率也是基于辐射能定义的最大热力学效率的一半[18].一个关于高低温热源均为有限尺寸的热机性能的系统性研究给出了热机工作在线性响应和非线性响应区域的优化途径[19,20].因此,热源有限尺寸的热设备的性能研究因其具有工程实践性价值已经成为有限时间热力学研究领域的一个重要课题。

然而,目前人们更多关注有限尺寸热源(或冷源)热机的性能优化问题,而对于高温热源尺寸无限而冷源尺寸有限的制冷机的性能研究较少,其实该制冷过程对应于一个有限尺寸的物体(冷源)被冷却到一个指定的目标温度而外部环境(热源)温度保持不变的一个热力学过程,这也是在工程实践中的常见过程.本文基于线性不可逆热力学理论,结合有限时间热力学方法,研究了一个有限尺寸低温热源的制冷机(保持高温热源无限)的工作执行,解析性地给出了该制冷机在紧耦合条件下的输入功率和制冷系数的表达式,并且进一步讨论了该制冷机的性能优化问题.本文的研究结果有助于人们深入理解制冷机的实际工作过程.

2 物理模型和公式

本文的制冷机模型如图1所示,假设该制冷机冷源的初始温度为Tc0,制冷的目标温度为Tcf,Th为高温热源的温度(保持不变),T是冷源在制冷过程中的温度,CV=CV(T)为冷源的等体热容量.当外界输入无限小功dA时,工质从冷源吸收的无限小热量为dQc,则该制冷机在工作过程中外界的输入功A为

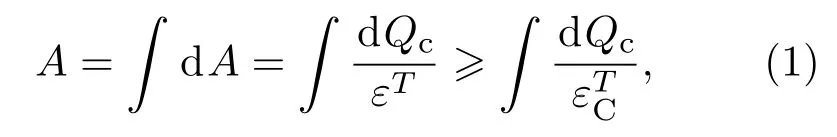
其中,εT是制冷系数,为对应该过程的卡诺制冷系数.一个闭合的热力学系统与其外界周围环境构成一个复合热力学系统,外界对这个复合热力学系统所做的最小功就是制冷机的辐射能.因此,外界输入制冷的最小功(也称辐射能)E为

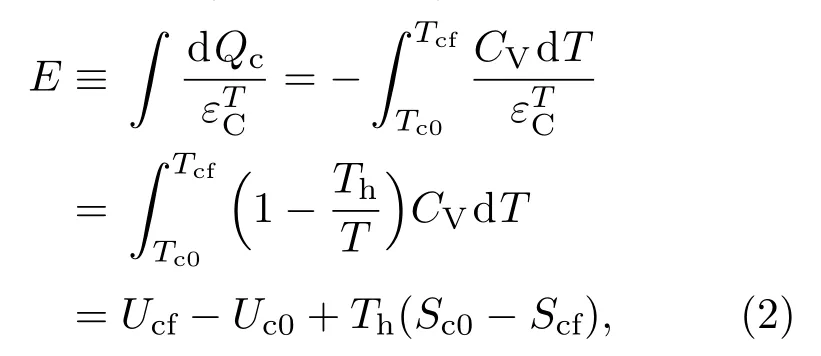
这里Ui(Si)(i=c0,cf)是冷源在初态和末态的内能(熵).在计算过程中使用了如下定义:

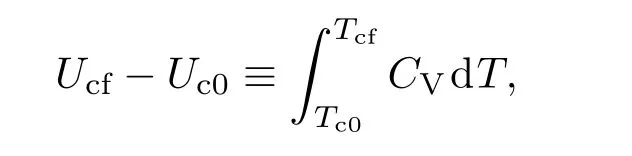
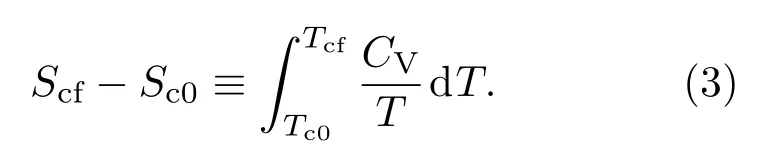
这样,制冷系数ε可以表示为

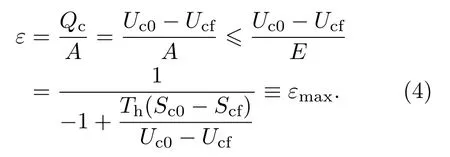
其中,εmax是工程上的最大热力学制冷系数.当CV→∞时(对应于一个等温过程),则(Uc0−Ucf)/Tc0=Qc/Tc0=Sc0−Scf,这样,εmax即为卡诺制冷系数εC=Tc0/(Th−Tc0).

图1 无限尺寸热源(温度为Th)而有限尺寸冷源的制冷机示意图这里,T为t时刻冷源的温度,CV为冷源的等体热容量Fig.1.Schematic plot of a refrigerator with an in fi nitesized hot reservoir(temperature Th)and a fi nite-sized cold one.Here,T is the temperature of the cold reservoir at time t,and CVis a heat capacity at constant volume.

基于局域平衡假设的线性不可逆热力学是一个较为完备的理论,能够描述近平衡态情况下宏观热力学系统的非平衡演化过程.因此,利用线性不可逆热力学方法,本文研究的制冷机的热力学流和力之间的关系可以表示为:

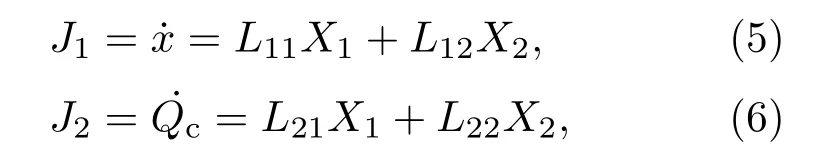
Lij(i,j=1,2)是Onsager系数,并且L12=L21.表示粒子流密度,为工质从冷源吸收的热流,“˙”表示对时间的导数.整个系统的熵产生率为

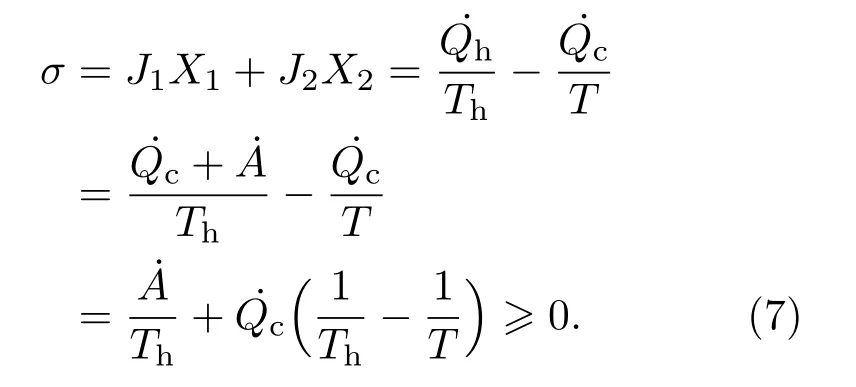
根据热力学第二定律,Onsager系数满足如下条件:

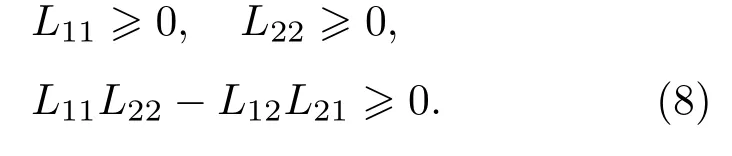
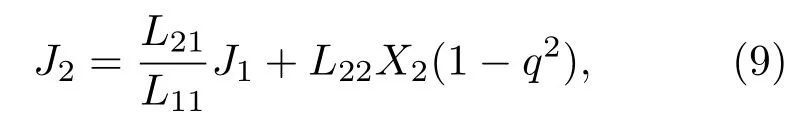
其中,q2为耦合系数

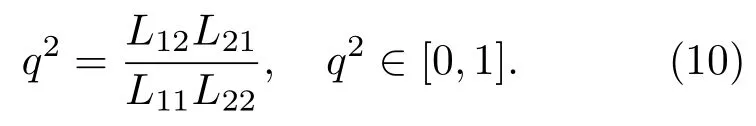
则流入高温热源的热流J3可以表示为

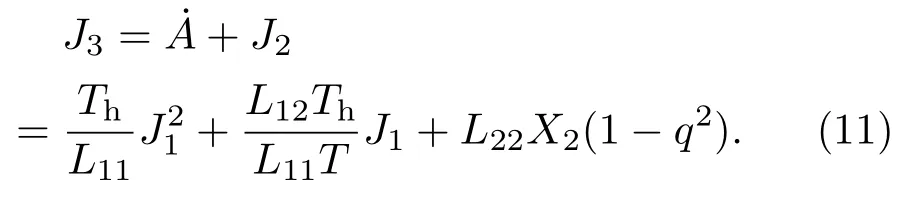
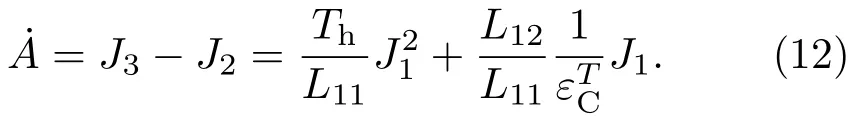
从初始时刻(t=0)到最终时刻(t=τ)的整个制冷过程中,外界输入的总功可写为

这里利用了如下公式:

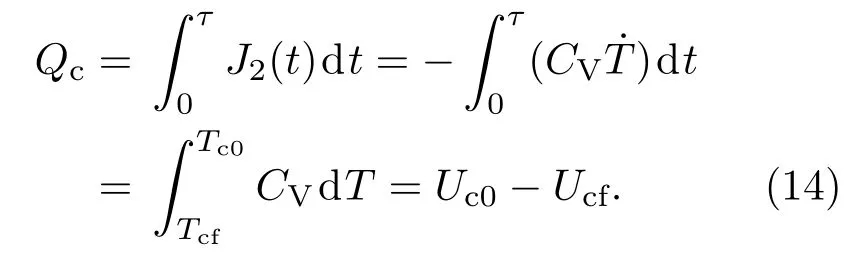
最后,外界输入的平均功率(P)和制冷系数(ε)分别表示为

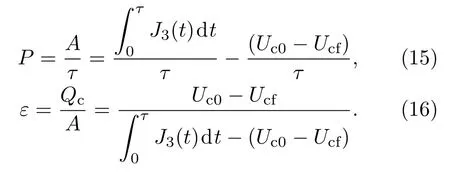
3 结果与讨论

从方程(15)和(16)可以看出,在制冷时间(τ)固定的情况下,对制冷机的性能优化可以转化为对于积分项的研究.在制冷机过程中,冷源内能的变化可以表示为

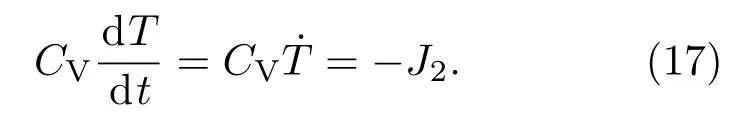
结合方程(9),J1(t)可以表示为

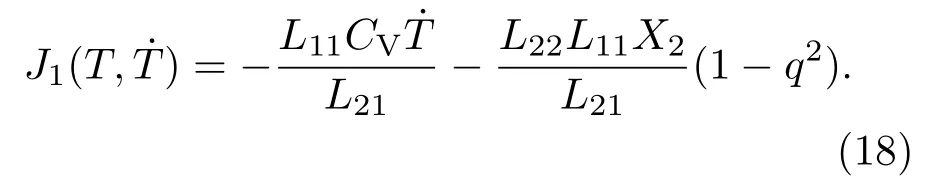
将方程(18)代入方程(11),J3(t)可以写为

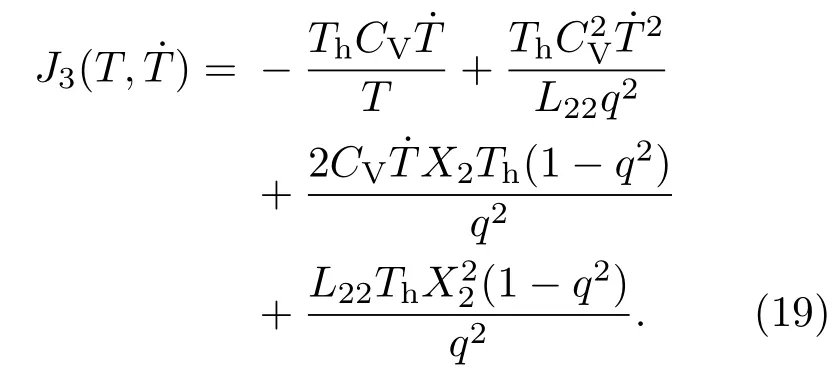
优化制冷机的目的就是使外界输入功最小,进而达到提高制冷系数的目的.这一过程就是使积分项最小化,并满足A＞0.根据欧拉-拉格朗日方程:

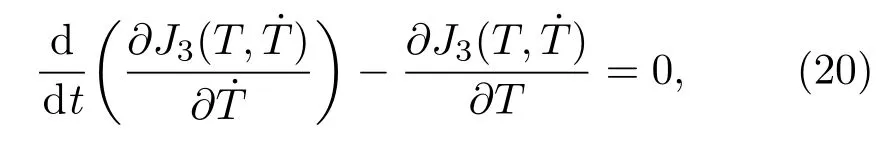
可以得到如下表达式

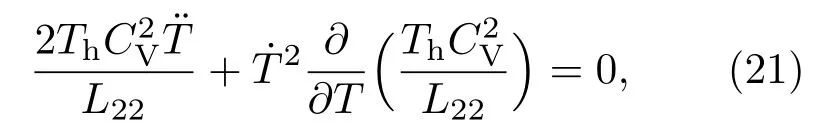
这里我们用到了紧耦合条件q2=1.因为在线性不可逆热力学中,广义流与广义力满足线性关系,热力学系统的重要信息反映在Onsager系数中,并且Onsager系数之间的关系可以通过耦合因子q2反映出来[见方程(10)],而紧耦合条件通常也是热机工作的最佳条件[3,21,22].

方程(21)可以进一步写为

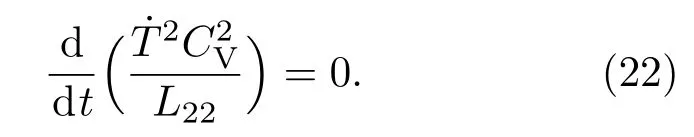
积分方程(22),可以得到

α为积分常数.对方程(23)积分,可以得到

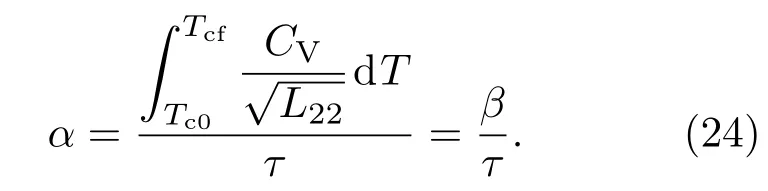
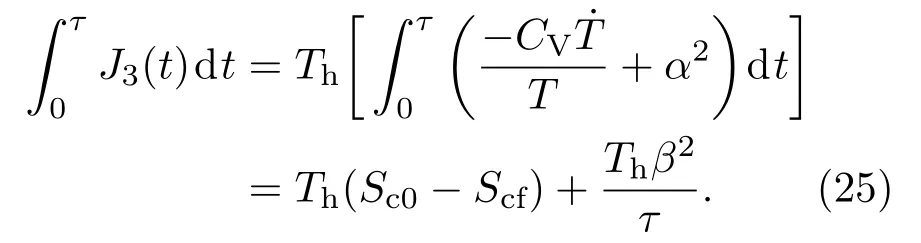
将方程(25)代入方程(15)和(16),平均功率和制冷系数可以表示为：

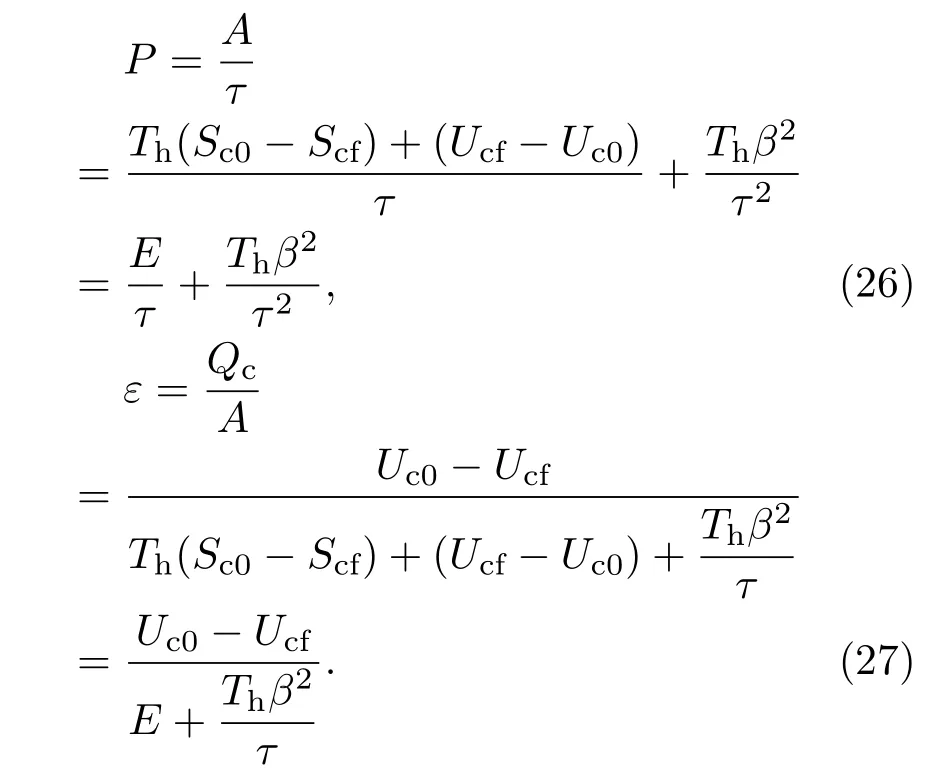
从方程(26)可以看出,平均功率P随着时间的增加呈现单调递减趋势,不存在平均功率P关于时间τ的最优值.这与文献[8]所述的高温热源无限而低温热源有限的热机情况不同,在那里最优功为辐射能的一半.当τ→∞时,则P→0(对应于准静态过程),此时ε=εmax=εC.实际上,对于一个真实的制冷过程,要求τ＞0且为有限值,利用方程(26)并且令Σ=Thβ2,可以得到

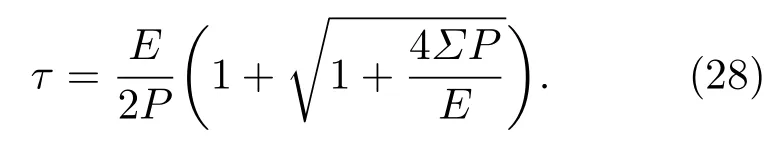
将方程(28)代入方程(27)并利用方程(4),可以得到制冷系数ε与功率P的关系为

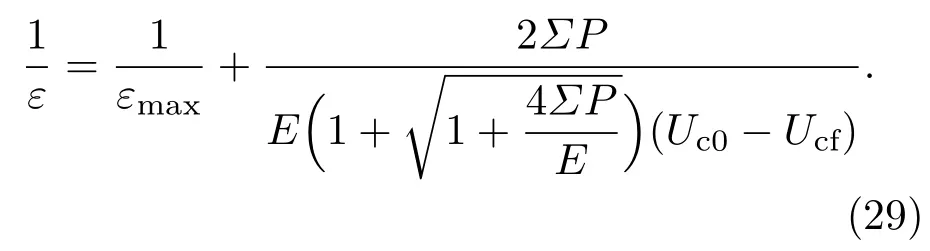
关系(29)式为进一步认识制冷系数与平均功率以及辐射能之间的关系提供了有力工具.为了能够更直观地反映制冷系数ε与P之间的关系,考虑到制冷机真实的工作过程,我们选择则一组参数:εmax=3,Σ=30 kJ·s,τ=30 s.给定辐射能(E)后,可以根据方程(26)和(27)粗略地估算出P的最小值和(Uc0−Ucf)的最大值.这样,不同辐射能(E)条件下,制冷系数(ε)随着平均功率(P)的演化行为清晰地反映在图2中.从图2可以看出,随着P的增加,ε呈现出明显的单调递减的特征.同时注意到,E的增加导致了制冷系数ε的增强.这样的行为可以理解如下:当P较小时,意味着时间τ很大,整个制冷过程趋近于准静态过程,制冷系数ε处于较大值,特别是当P→0时,ε→εmax(如图2所示).P的增加意味着τ的减少,制冷过程逐渐远离准静态过程而接近于不可逆的真实过程,这导致制冷系数呈现出逐渐减小的特征.与之相反,辐射能的增加使得ε呈现出增加的特征.从(26)式可以看出,当平均功率P保持不变时,E的增大意味着τ的增加,这导致制冷过程的进程缓慢,表现出越来越趋近于准静态行为,因此ε呈现出增加行为.从上述分析可以看出,对于一个低温热源有限的制冷过程,必须根据周围环境的实际情况和热设备的具体参数来设计制冷方案,以合适的输入功率达到较佳的制冷目的.

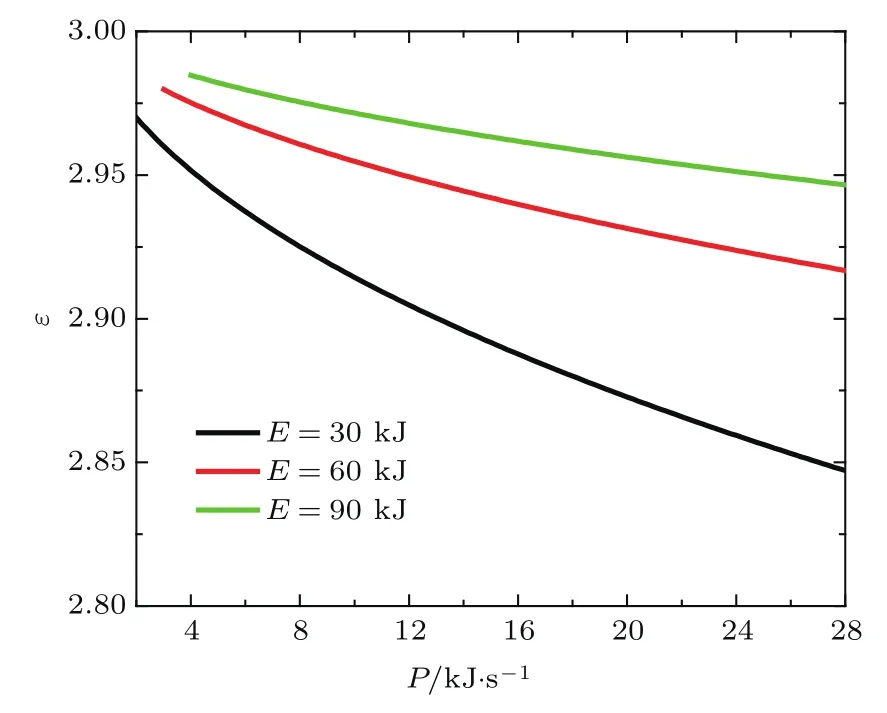
图2 E取不同值时制冷系数ε与功率P的关系其中,εmax=3,Σ =30 kJ·s,τ =30 sFig.2. The coefficient of performance ε versus the power P for different E.Here,εmax=3,Σ =30 kJ·s,τ=30 s.

4 结论

工作在有限尺寸的高低温热源之间的热设备的性能优化是有限时间热力学领域中的一个重要研究课题.本文提出了一个高温热源保持不变而低温热源为有限尺寸的制冷机模型,结合有限时间热力学和线性不可逆热力学理论详细地分析了该制冷机的特性.我们解析性地给出了在制冷目标温度一定情况下的外界输入功率和制冷系数表达式,并且进一步讨论了这种较为真实的热力学过程.发现在环境(高温热源)温度不变而冷源温度变化的情况下,外界的输入功率与制冷时间的关系不存在明确的优化关系,这是与高温热源尺寸有限而冷源尺寸无限的热机工作过程的一个显著区别.进一步发现制冷系数随着输入功率的增加呈现出单调减小的特征,而辐射能的增加导致了制冷系数的增强.这种输入功率与制冷系数的变化关系是不可逆过程和准静态过程相互竞争的反映.本文的研究结果不仅有助于深入理解高温热源尺寸无限而冷源尺寸有限的制冷机的工作过程,而且对于在工程热力学上如何根据具体情况来设计热装置进而达到优化制冷也有帮助.本文的方法也可以应用到热泵性能的研究.另外,时间反演破坏会导致紧耦合条件不再成立,更多的物理内容有待进一步研究.

[1]Curzon F,Ahlborn B 1975Am.J.Phys.43 22

[2]Vaudrey A,Lanzetta F,Feidt M 2014J.Non-Equil.Therm.39 199

[3]van den Broeck C 2005Phys.Rev.Lett.95 190602

[4]Andresen B 2011Angew.Chem.Int.Ed.50 2690

[5]Ding Z M,Chen L G,Wang W H,Sun F R 2015Sci.Sin.Technolog.45 889(in Chinese)[丁泽民,陈林根,王文华,孙丰瑞2015 中国科学:技术科学45 889]

[6]Bi Y H,Chen L G 2017Optimal Peformamnce of Gas Heat Pumps With the Framework of Finite-time Thermodynamics(Beijing:Science Press)pp1–20(in Chinese)[毕月虹,陈林根2017 空气热泵性能有限时间热力学优化(北京:科学出版社)第1—20页]

[7]Gordon J M,Huleihil M 1991J.Appl.Phys.69 1

[8]Bejan A 1996J.Appl.Phys.79 1191

[9]Lu C C,Bai L 2017Acta Phys.Sin.66 130501(in Chinese)[卢灿灿,白龙 2017物理学报 66 130501]

[10]Johal R S 2017Phys.Rev.E96 012151

[11]Yan H,Guo H 2012Phys.Rev.E86 051135

[12]Sheng S,Tu Z C 2014Phys.Rev.E89 012129

[13]Ondrechen M J,Rubin M H,Band Y B 1983J.Chem.Phys.78 4721

[14]Ondrechen M J,Andresen B,Mozurkewich M,Berry R S 1981Am.J.Phys.49 681

[15]LeffH S 1987Am.J.Phys.55 701

[16]Andresen B,Berry R S,Ondrechen M J,Salamon P 1984Acc.Chem.Res.17 266

[17]Yan Z,Chen L X 1997J.Phys.A:Math.Gen.30 8119

[18]Izumida Y,Okuda K 2014Phys.Rev.Lett.112 180603