双能谷效应对N型掺杂Si基Ge材料载流子晶格散射的影响∗
2018-03-26黄诗浩谢文明汪涵聪林光杨王佳琪黄巍李成
黄诗浩 谢文明 汪涵聪 林光杨 王佳琪 黄巍 李成
1)(福建工程学院,信息科学与工程学院,福州 350118)
2)(厦门大学,物理科学与技术学院,厦门 361005)
1 引 言
虽然Ge与Si同属于间接带隙材料,发光效率低,但是室温下Ge的直接带与间接带差值仅为136 meV,仍有少量电子占据其直接带能谷中,并且这些电子具有较高的辐射复合速率.同时,Si基Ge材料由于在光通信波段吸收系数大,具有能带结构可调的特点,并且和传统的硅互补金属氧化物半导体工艺相兼容等优点,所以Si基Ge材料一直以来都是科学家制备高效Si基光源的首选方案.
目前,国内外研究小组[1−10]都投入了大量的人力物力在Si基Ge高效发光材料与器件的开发上攻克了许多关键技术,但是在研究制备发光器件的过程中遇到了诸如激光器阈值电流密度过大、发光效率偏低、器件工作不稳定等难以解决的问题.为了突破在实验研究过程中遇到的一系列瓶颈,亟待从理论方面展开深入研究.当前,国内外对Si基Ge高效发光材料的理论研究主要集中于两方面:一是通过不同的计算方法研究应变对Ge能带结构的影响,预测Ge由间接带隙材料转变为直接带隙材料所施加的应力值大小[11−13];二是通过简化模型计算Ge材料的光增益情况[14,15];而对载流子在Si基Ge材料中的散射研究相对较少.
载流子的散射过程不仅影响着材料的电学性质,如载流子迁移率大小,而且与半导体材料的光学性质也息息相关.载流子的散射过程所需时间很短,发生于各种复合过程之前.类似于GaAs材料,Si基Ge材料的导带也有其独特的双能谷结构(直接带Γ能谷与间接带L能谷),载流子在双能谷之间的谷间散射有可能提高直接带载流子的占有率,进而提高直接带辐射复合效率.因此载流子的散射机制是深入研究Si基Ge材料光电性质的重要理论基础,对探索增强Si基Ge材料直接带发光效率的机理以及实现光增益的有效途径具有重要的科学意义.
本文从载流子散射机制的量子力学理论出发,构建载流子在Si基Ge材料导带双能谷结构中的不同晶格振动散射模型,建立相应的载流子散射率及平均弛豫时间模型,并进行数值计算,其量化结果可为设计与模拟Si基Ge器件提供理论参考.
2 晶格散射的量子模型
晶格散射是由于晶体中的原子在其平衡位置附近做微振动引起的.这种微振动可以用格波来描述.具体地,对于Ge有三个声学波(两个横声学波,TA和一个纵声学波,LA)和三个光学波(两个横光学波,TO和一个纵光学波,LO).格波的能量是量子化的,量子化的能量称为晶格振动能量的量子或声子.声子是玻色子,不具有物理动量,但是携带有准动量,并具有能量,是个准粒子.载流子在Si基Ge材料中被格波散射可以认为电子和声学声子或光学声子的相互作用.
由量子力学理论可知,载流子在晶格中的运动会受到附加势场的作用,比如晶格振动产生的简谐微扰势、电离杂质产生的库仑势、无序合晶产生的相干势等[16].假设这些偏离理想周期势的附加势可以写成V(x,t),则系统的哈密顿量可以写成H=H0+V(x,t),其中H0为无微扰时的哈密顿量,通过求解含时薛定谔方程:就可以得到在附加势的作用下载流子由状态k散射到状态k′的散射率W(k,k′).
对于声学声子散射,其附加势可以写成
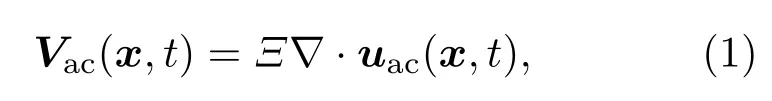
为形变势参数,∇·uac(x,t)给出相对体积形变,uac(x,t)代表晶体中x点的位移.波矢为q的长声学波可以由下式描述:
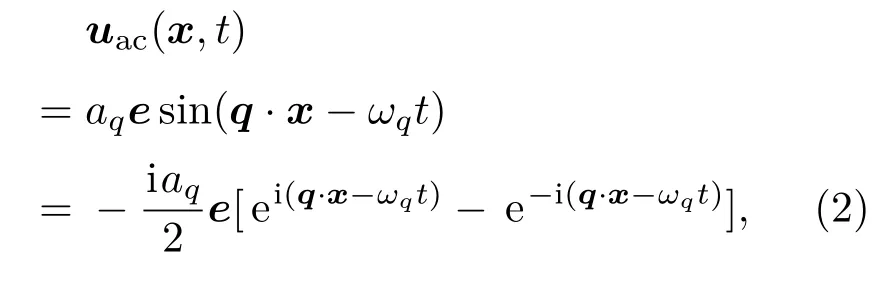
式中e为沿振动方向的单位矢量,aq为振幅,波矢为q的长声学波对应的频率为ωq.由此可得到附加势:
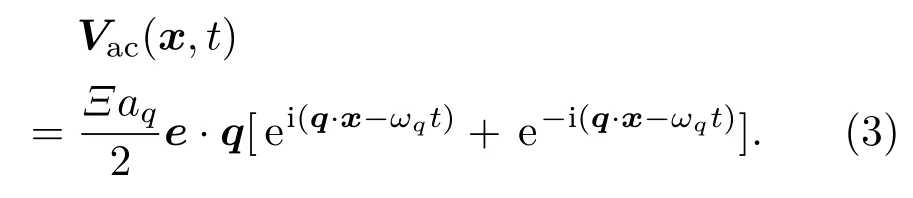
对于光学声子散射,其附加势可以写成:
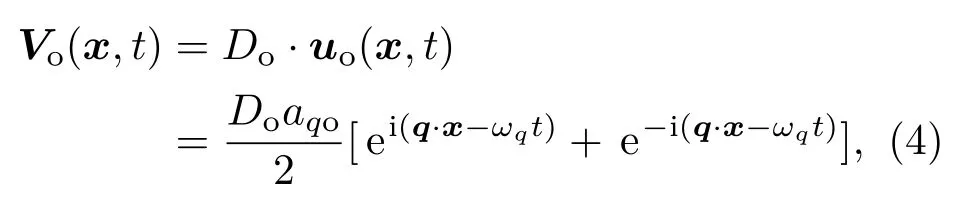
式中Do为光学形变势参数,aqo为振幅,uo(x,t)为不等价原子之间的相对位移.
2.1 直接带Γ能谷谷内声子散射
在直接带Γ能谷中,由于横波e⊥q,e·q=0,不产生形变势,所以TA声子不参与散射,对于纵声学波e·q=q,产生形变势,LA声子参与散射.在金刚石结构晶体中,光学波引起的两类不等价原子的相对移动并不会使位于k=0的能带带边发生正比于相对位移的一级移动;因此,在Γ能谷中,光学波形变势散射的作用很微弱,可不予考虑.所以在Si基Ge材料的直接带Γ能谷中谷内散射只有LA声子参与[16].
将直接带Γ能谷声学声子散射附加势的具体形(3)式,代入含时薛定谔方程,求解可得直接带Γ能谷中谷内LA声子散射率表达式:

2.2 间接带L能谷谷内散射
Si基Ge材料导带底位于布里渊区的边界〈111〉方向上的L点处,其等能面由4个旋转椭球面构成.由跃迁选则定则可知,TA,LA,TO和LO声子均可参与间接带L能谷载流子的谷内散射[16].
由于声学声子的能量约为几meV,因此在求解声学声子的散射过程中,可不考虑散射中电子能量的变化,将声学声子散射近似当作弹性散射.同时,室温下电子能量相应的波矢值约占简约布里渊区线度的几十分之一,因此可近似认为只有长波声子参与谷内散射.
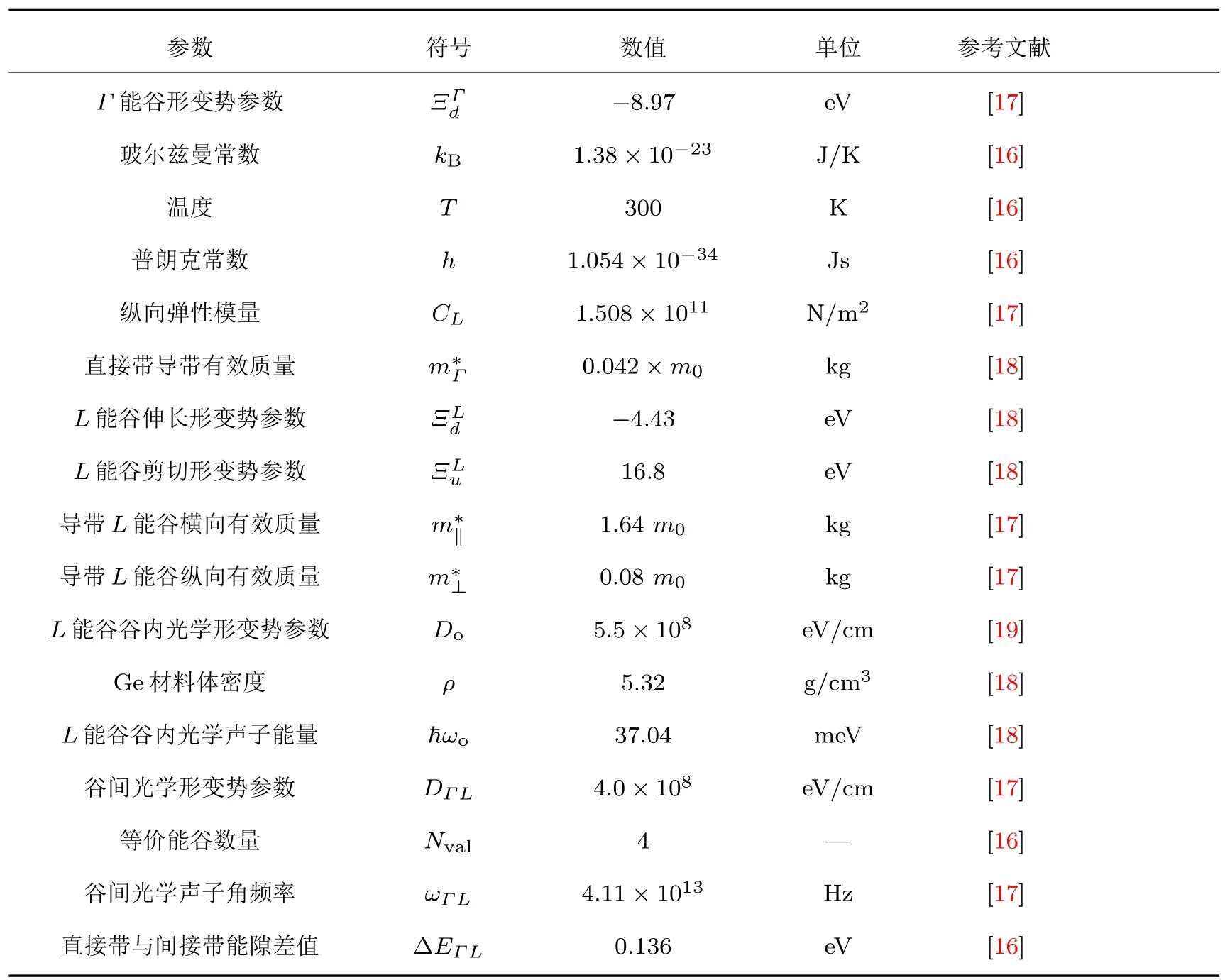
表1 本文相关参数及其数值Table 1.Parameters for the lattice scattering in n-type Ge-on-Si.
类似于直接带Γ能谷声学声子散射形式,间接带L能谷声学声子散射可分为横声学声子散射和纵声学声子散射,其散射率表达式分别为[16]:
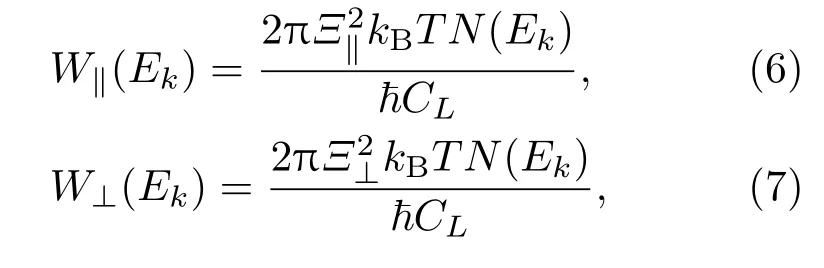
式中,
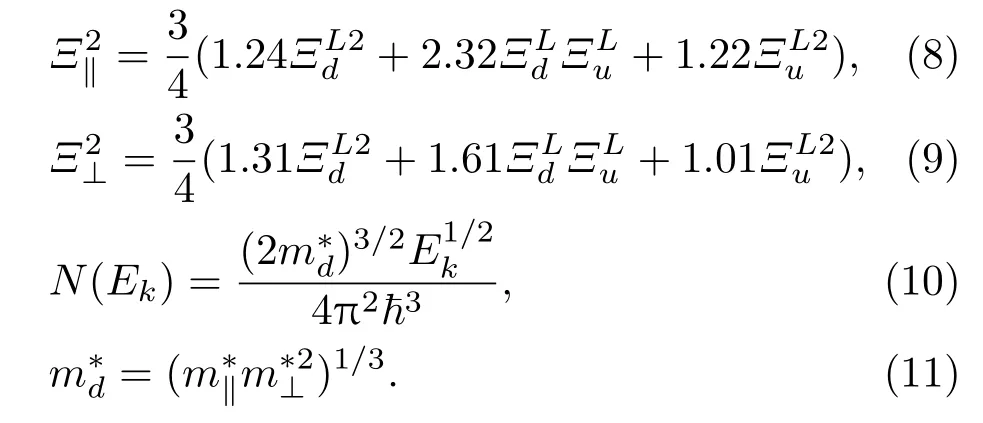
不同于声学波散射,光学波散射所涉及的声子能量比长波声学声子高,约为几十meV数量级,和室温下的电子能量有相同数量级.因此这类散射属于非弹性散射.在光学波谷内散射中,各个方向的散射所涉及的光学声子的波矢分布在布里渊区中心附近很小的范围内,也属于长波声子.对于Si基Ge材料,晶胞内两种不等价原子之间的纵光学振动不会引起极化现象,属于非极性光学声子散射.
将间接带L能谷的谷内光学声子散射附加势的具体形(4)式,代入含时薛定谔方程,可得谷内光学声子散射率为[16]:
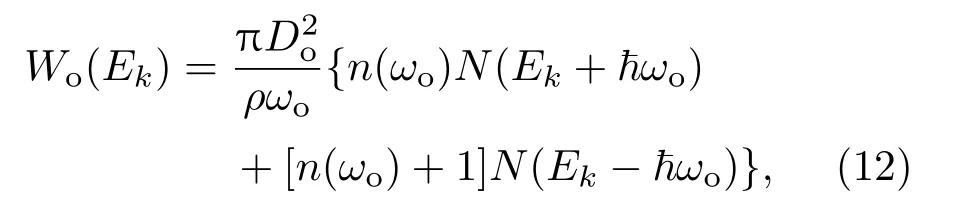
式中前一项表示吸收谷内光学声子的跃迁过程,后一项表示发射谷内光学声子的跃迁过程,温度为T时的平均声子数为:
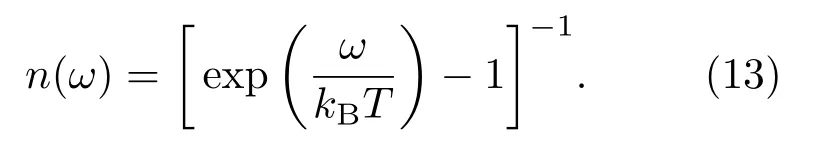
2.3 双能谷(Γ能谷与L能谷)的谷间散射
发生谷间散射时,电子波矢要发生很大的改变,即准动量有相当大的变化;因此谷间散射可认为与短波声子发生作用.同时与谷内光学声子散射类似,谷间光学波散射所涉及的声子能量通常也为几十meV数量级,因此谷间散射属于非弹性散射.
类似于谷内光学波散射,可以引入谷间形变势常量DΓL来描述谷间散射,因此可以得到类似于谷内光学波散射的表达形式[16]:
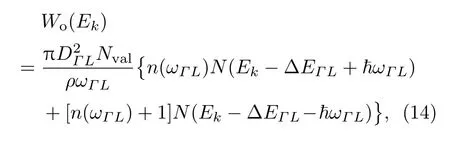
式中前一项表示吸收谷间光学声子的跃迁过程,后一项表示发射谷间光学声子的跃迁过程,N(Ek)为跃迁终态能谷的能量状态密度.
2.4 载流子平均弛豫时间
散射率反映了单位时间内载流子发生散射的次数,它与载流子的动量弛豫时间τ(E)互为倒数关系,均体现了载流子的个体性质.在分析载流子的输运情况时,人们往往更关注载流子的统计性质,即载流子的平均弛豫时间(也称为平均散射时间、平均自由时间),它与载流子的散射概率互为倒数关系,被定义为[16]:
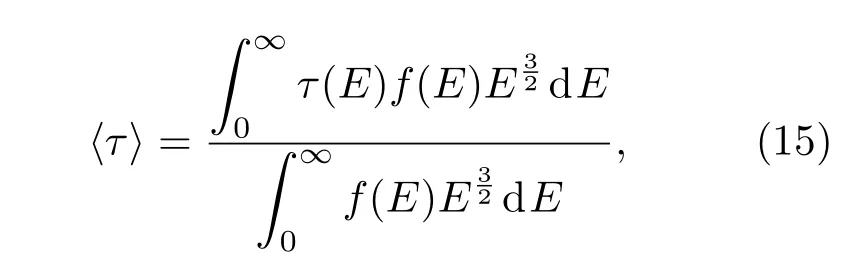
式中,

3 结果与讨论
室温下,直接带Γ能谷LA声子的散射率随电子能量的变化如图1(a)所示.对于单个电子而言,电子能量越高,发生LA声子的散射率越大.图1(b)为Γ能谷电子的平均散射时间随电子浓度的变化关系,可见当电子浓度达到中等掺杂浓度后(大于1018cm−3),随着浓度的增高,平均弛豫时间将减小,其散射概率增大.

图1 直接带Γ能谷LA声子(a)散射率随电子能量的变化,(b)散射时间随电子浓度的变化Fig.1.(a)scattering rates as a function of the energy and(b)average scattering time as a function of the n-type doping concentrations in the case of Γ valley for longitudinal modes.
间接带L能谷LA和TA声子的散射率随电子能量的变化以及散射时间随电子浓度的变化如图2所示.与直接带Γ能谷LA声子类似,电子能量越高,声子散射率越大;电子的平均散射时间随着浓度的增大而减小,其散射概率增大;同时可见,LA声子的贡献稍大于TA声子,这一结论与实验观测到的结果[20]一致,进一步验证了理论计算的正确性.
间接带L能谷谷内光学声子散射情况计算结果如图3所示.光学声子散射可分为吸收光学声子散射和发射光学声子散射.从图3(a)可知,当电子能量大于谷内光学声子能量时,发射谷内光学声子才有可能发生;并且发射光学声子散射、吸收光学声子散射以及总散射的散射率随着电子能量的增加而增大;与吸收谷内光学声子散射相比,电子能量越高,电子更倾向于发射谷内光学声子散射.
图3(b)显示,当电子浓度大于1017cm−3时,随着电子浓度的增加,吸收光学声子的概率增大,发射光学声子的概率减小.这一规律反映了N型掺杂Si基Ge材料通过适当的掺杂可以有效地提高直接带导带底电子的占有率.一方面,掺杂浓度提高,电子吸收谷内光学声子的概率增大,可以跃迁到间接带L能谷更高的能级,进而有可能通过谷间光学声子的散射方式,二次跃迁到直接带Γ能谷,从而提高直接带导带底电子的占有率.另一方面,从散射的量子力学推导过程发现,L能谷到Γ能谷的谷间光学声子散射与谷内光学声子散射的规律是类似的(但是目前缺乏L能谷到Γ能谷的谷间散射光学形变势能的实验数据报道),因此,从L能谷到Γ能谷的谷间光学声子散射也将遵循电子浓度增加吸收谷间光学声子的概率增大这一规律,从而将有更多的电子从L能谷散射到Γ能谷,提高直接带导带底电子占有率.
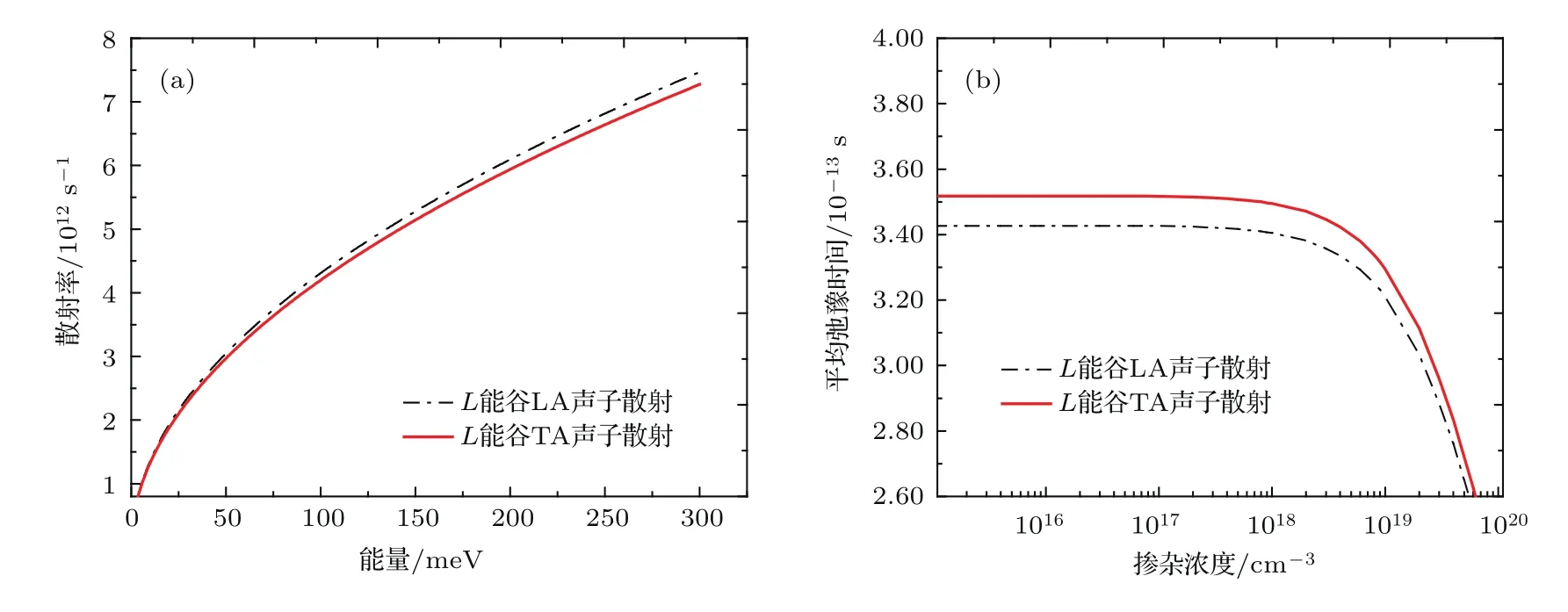
图2 L能谷LA,TA声子(a)散射率随电子能量的变化,(b)散射时间随电子浓度的变化Fig.2.(a)Scattering rates as a function of the energy and(b)average scattering time as a function of the n-type doping concentrations in the case of L valleys for longitudinal modes and transverse modes.
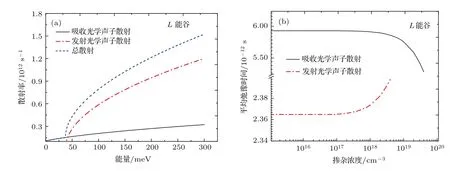
图3 间接带L能谷谷内光学声子(a)散射率随电子能量的变化,(b)平均散射时间随电子浓度的变化Fig.3.(a)scattering rates as a function of the energy and(b)average scattering time as a function of the n-type doping concentrations in the case of L valleys for optical phonon scattering in intra-valley processes.
电子从Γ能谷跃迁到L能谷的谷间散射过程如图4.同样,电子能量越高,散射率越大.相比于吸收谷间光学声子散射,电子在Γ能谷更倾向于发射谷间光学声子跃迁到L能谷.当电子浓度大于1019cm−3时,随着电子浓度的增加,电子发射或吸收谷间光学声子跃迁到间接带L能谷的概率增大,这种情况将不利于直接带发光.
综上所述,N型掺杂Si基Ge材料导带电子从Γ能谷散射到L能谷与从L能谷跃迁到Γ能谷具有竞争的关系.当掺杂浓度界于1017cm−3到1019cm−3时,适当提高N型掺杂浓度有利于提高直接带导带底电子占有率.但是,由于L能谷到Γ能谷的谷间散射光学形变势能参数目前没有相关理论或实验数值报道,因此有待后续进一步深入研究.
本文计算得到的低掺杂浓度情况下L能谷、Γ能谷电子的平均弛豫时间如表2和表3所列.文献[21,22]采用透射实验的方法测量到体Ge材料电子从Γ能谷散射到L能谷的谷间散射时间为(230±25)fs;文献[23]报道了Ge/SiGe量子阱系统中电子从Γ能谷散射到L能谷的谷间散射时间为185 fs.本文计算得到Γ能谷到L能谷的谷间散射时间为216 fs,与文献报道值一致,进一步证实了本文计算结果的正确性.
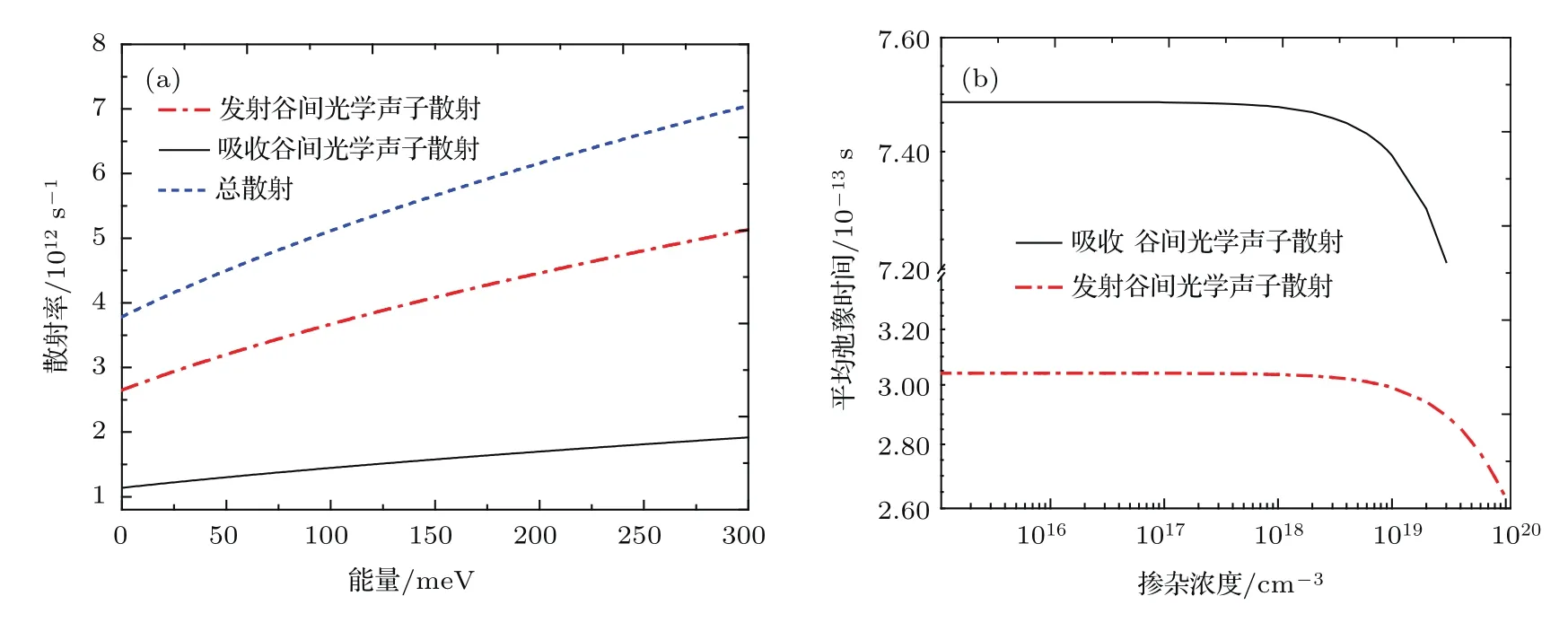
图4 谷间光学声子(a)散射率随电子能量的变化,(b)散射时间随电子浓度的变化Fig.4.(a)Scattering rates as a function of the energy and(b)average scattering time as a function of the n-type doping concentrations in the case of inter-valley processes for optical phonon scattering.

表2 L能谷电子平均弛豫时间比较Table 2.Comparison of average scattering time for acoustic and optical phonon scattering in the case of L valleys.

表3 Γ能谷电子平均弛豫时间比较Table 3.Comparison of average scattering time for acoustic phonon scattering in Γ valley and for inter-valley optical phonon scattering from Γ valley to L valleys.
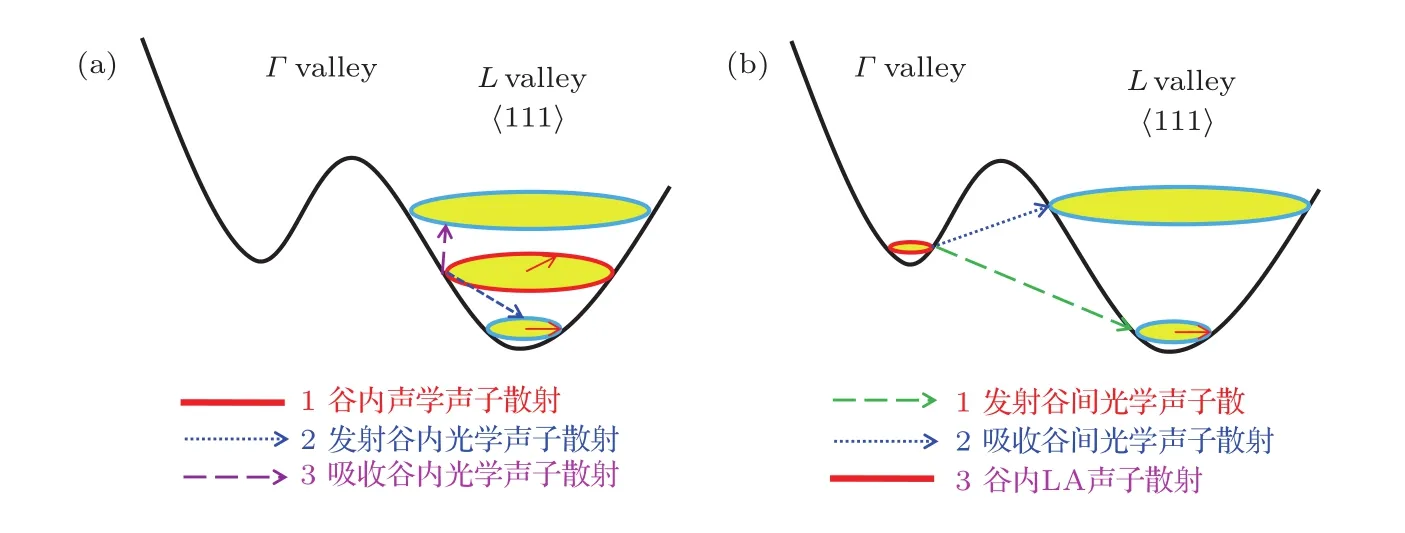
图5 (a)L能谷电子散射机制示意图;(b)Γ能谷电子散射机制示意图Fig.5.Schematically illustrate the phenomenon of carrier scattering in(a)L valleys and(b)Γ valley.
通过表2和表3电子平均弛豫时间的比较,可以得到L能谷、Γ能谷电子散射机制,如图5示意.图5(a)表示处于L能谷的电子优先通过谷内声学声子散射的方式弛豫能量,其次通过发射谷内光学声子散射的方式弛豫到间接带更低的能级,最后有可能通过吸收谷内光学声子散射的方式跃迁到间接带更高能级.图5(b)表示处于Γ能谷的电子优先通过发射谷间光学声子散射到间接带L能谷,其次通过吸收谷间光学声子散射到间接带L能谷,最后通过LA声子散射的方式发生动量与能量的弛豫.
4 结 论
载流子在半导体中的散射过程需要的时间很短,往往发生于各种复合之前.本文研究了载流子在N型掺杂Si基Ge材料导带双能谷结构中的晶格散射机制.结果表明,处于L能谷的电子通过吸收声子的散射方式跃迁到直接带Γ能谷是增强N型掺杂Si基Ge材料直接带发光效率的有效途径之一.计算结果可为提升Si基Ge光电子材料与器件的性能提供理论指导和实验依据.
[1]Koerner R,Oehme M,Gollhofer M,Schmid M,Kostecki K,Bechler S,Widmann D,Kasper E,Schulze J 2015Opt.Express23 14815
[2]Lin G Y,Chen N L,Zhang L,Huang Z W,Huang W,Wang J Y,Xu J F,Chen S Y,Li C 2016Materials9 803
[3]Lin G Y,Yi X H,Li C,Chen N L,Zhang L,Chen S Y,Huang W,Wang J Y,Xiong X H,Sun J M 2016Appl.Phys.Lett.109 141104
[4]Kaschel M,Schmid M,Gollhofer M,Werner J,Oehme M,Schulze J 2013Solid-State Electron83 87
[5]Camacho-Aguilera R E,Cai Y,Patel N,Bessette J T,Romagnoli M,Kimerling L C,Michel J 2012Opt.Express20 11316
[6]Liu J F,Sun X C,Camacho-Aguilera R,Kimerling L C,Michel J 2010Opt.Lett.35 679
[7]Liu Z,Hu W X,Li C,Li Y M,Xue C L,Li C B,Zuo Y H,Cheng B W,Wang Q M 2012Appl.Phys.Lett.101 231108
[8]Saito S,Al-Attili A Z,Oda K,Ishikawa Y 2016Semicond.Sci.Technol.31 043002
[9]Huang S H,Li C,Chen C Z,Wang C,Xie W M,Lin S Y,Shao M,Nie M X,Chen C Y 2016Chin.Phys.B25 066601
[10]Bao S,Kim D,Onwukaeme C,Gupta S,Saraswat K,Lee K H,Kim Y,Min D,Jung Y,Qiu H,Wang H,Fitzgerald E,Tan S C,Nam D 2017Nat.Commun.8 1845
[11]Kurdi M E,Fishman G,Sauvage S,Boucaud P 2010J.Appl.Phys.107 013710
[12]Liu L,Zhang M,Hu L J,Di Z F,Zhao S J 2014J.Appl.Phys.116 113105
[13]Dutt B,Sukhdeo D S,Nam D,Vulovic B M,Yuan Z,Saraswat K C 2012IEEE Photon.J.4 2002
[14]Chow W W 2012Appl.Phys.Lett.100 191113
[15]Huang S H,Li C,Chen C Z,Zheng Y Y,Lai H K,Chen S Y 2012Acta Phys.Sin.61 036202(in Chinese)[黄诗浩,李成,陈城钊,郑元宇,赖虹凯,陈松岩 2012物理学报61 036202]
[16]Ridley B K 2013Quantum Processes in Semiconductors(Oxford:Oxford University Press)
[17]Lever L,Ikonic Z,Valavanis A,Kelsall R W,Myronov M,Leadley D R,Hu Y,Owens N,Gardes F Y,Reed G T 2012J.Appl.Phys.112 123105
[18]Fischetti M V,Laux S E 1996J.Appl.Phys.80 2234
[19]Wang X X,Li H F,Camacho-Aguilera R,Cai Y,Kimerling L C,Michel J,Liu J F 2013Opt.Lett.38 652
[20]Herring C,Vogt E 1956Phys.Rev.101 944
[21]Mak G,Driel H 1994Phys.Rev.B49 16817
[22]Zhou X Q,Driel H,Mak G 1994Phys.Rev.B50 5226
[23]Claussen S A,Tasyurek E,Roth J E,Miller D 2010Opt.Express18 25596
