金刚石氮空位色心耦合机械振子和腔场系统中方差压缩研究∗

廖庆洪 叶杨 李红珍 周南润

1)(南昌大学电子信息工程系,南昌 330031)

2)(清华大学,低维量子物理国家重点实验室,北京 100084)

3)(西安交通大学应用物理系,西安 710049)

1 引 言

随着纳米技术的不断进步,机械振子的尺寸已经可以做到微米甚至纳米量级.纳米机械振子有着较高的振动频率和品质因子、极小的质量以及较低的耗散,在高精度位移测量、力测量、质量测量和精确的量子计算等方面有着重要的应用[1−4].此外,机械振子可以用来研究宏观系统的量子特性,比如宏观量子叠加态、量子纠缠态、以及用于量子信息处理等.要让纳米机械振子在如此广泛的应用中都发挥作用,人们希望能更加方便地操控其状态.因此,如何把机械振子与一个两能级系统耦合起来,实现强耦合就很值得研究[5].另一方面,在固态系统中,金刚石氮空位中心(NV色心)在室温下具有毫秒量级的长相干时间,也很容易被微波操控,并被激光高效率地读出其状态,是实现量子计算的优良载体,被认为有望实现室温下的量子计算和高灵敏度量子测量以及在量子信息处理、纳米尺度空间中的磁场与电场、温度的灵敏探测等相关领域具有巨大的应用价值[6].把金刚石氮空位中心与纳米机械振子耦合起来,用于精密测量,量子信息处理等成为了一个热门的研究题目[5].利用梯度磁场诱导的金刚石NV色心与微纳米机械振子运动之间的耦合,实现了百纳米尺度的金刚石质心振动与其中的色心电子自旋之间的强耦合,并且制备了金刚石NV色心的薛定谔猫态和实现双缝物质波干涉[7].文献[8]提出了基于金刚石NV色心与机械振子的耦合,利用动力学解耦技术实现超灵敏质量探测方案.基于Stark效应的高灵敏度电场探测[9],基于NV色心的光检测磁共振谱峰值随着温度的变化而变化,可实现纳米尺度的高灵敏度温度探测[10],NV色心与外部机械振子以及所在的金刚石机械振子耦合分别可以实现髙灵敏度的机械振子运动[11]以及金刚石内部的应力等[12]物理量探测.Li等[13]理论上提出了利用通电的碳纳米管机械振子和单个NV色心自旋耦合的混合型量子器件,实现了NV色心单自旋体系与纳米机械振子强耦合机制及相干操控.文献[14]研究了借助两能级发射器由真空涨落引起的能级移动探索振动石墨烯机械振子位移在量子水平的压缩和测量方案.文献[15,16]研究了超导量子比特耦合NV色心系综系统中的量子态的传输和存储以及存在内相互作用的多体开放量子系统中的纠缠动力学特性.

本文研究金刚石NV色心同时耦合腔场和机械振子系统中机械振子的方差压缩,主要讨论金刚石NV色心初态和NV色心与机械振子耦合强度对声子场方差压缩的影响.结果发现:控制和操纵系统参数可以制备压缩时间长、压缩幅度大的声子场压缩态,并且通过调控NV色心初态以及磁场梯度可以实现对机械振子方差压缩非经典特性的操控.

2 物理模型及其基本方程

本文研究光悬浮的纳米金刚石(内含单个NV色心)系统[7],物理模型如图1所示,纳米金刚石囚禁在谐振势中,囚禁纳米金刚石振动频率为ωm,质量为m,纳米金刚石质心运动哈密顿量可以描述为若外加磁场具有梯度,则导致金刚石NV色心与纳米金刚石质心运动的耦合,耦合哈密顿量为考虑金刚石NV色心和腔场相互作用,其相互作用哈密顿量为同时金刚石NV色心由外加激光场驱动,则系统的哈密顿量为

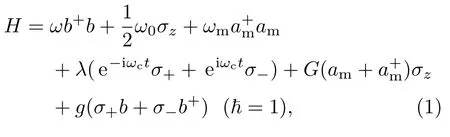
其中,ω为腔场频率,ω0为金刚石NV色心跃迁频率,ωc为经典驱动场频率;g为金刚石NV色心与腔场的耦合系数;λ为NV色心与经典驱动场的耦合系数;G=gsµBGma0/ħ为NV色心与机械振子的耦合系数;Gm为磁场梯度;b+和b分别为腔场的产生和湮灭算符;|0〉和|1〉构成量子比特,分别对应σz=−1和σz=+1的本征矢[8],令|0〉=|g〉,|1〉=|e〉,则σ+=|e〉〈g|和σ−=|g〉〈e|分别为金刚石NV色心的上升和下降算符.

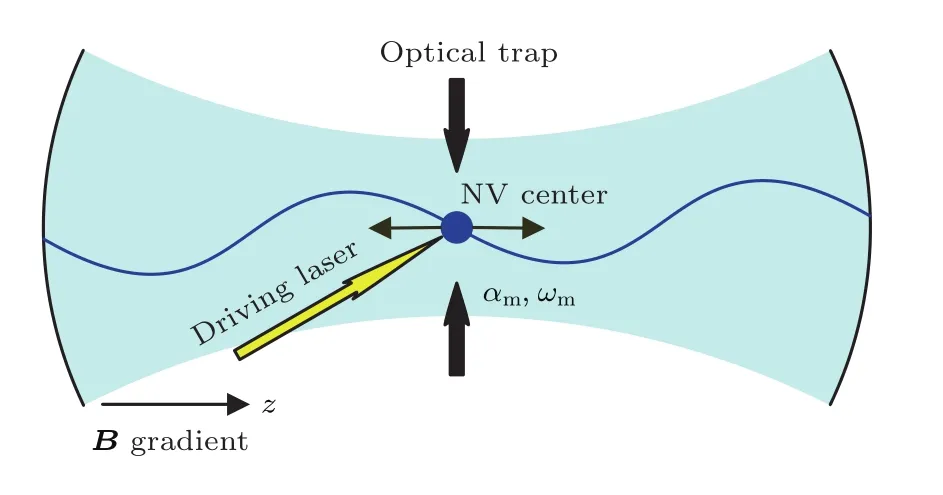
图1 金刚石NV色心耦合腔场和机械振子模型示意图Fig.1.Schematic diagram of nitrogen-vacancy center in diamond coupled to cavity field and mechanical resonator.

因为幺正变换不会改变系统的本征值,引入一个幺正变换U1=exp(−iωcσzt/2),将(1)式的哈密顿量变换到旋转坐标表象中,则

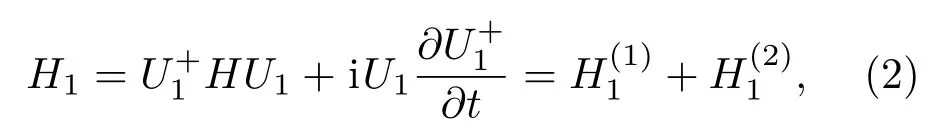
其中

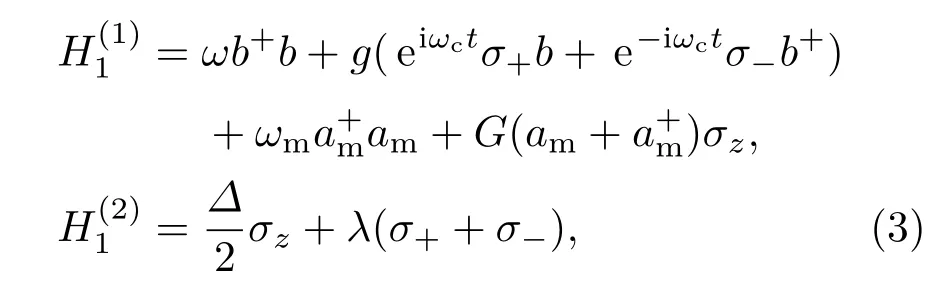
式中Δ=ω0−ωc为金刚石NV色心跃迁频率与NV色心驱动场频率的失谐量.

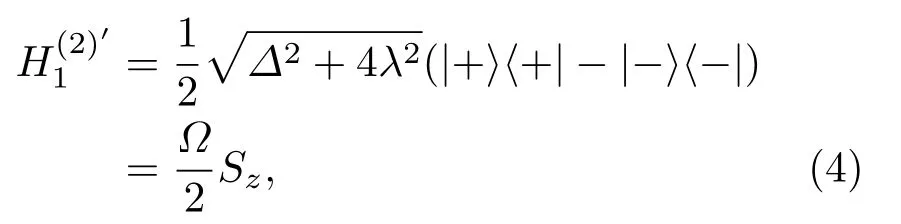
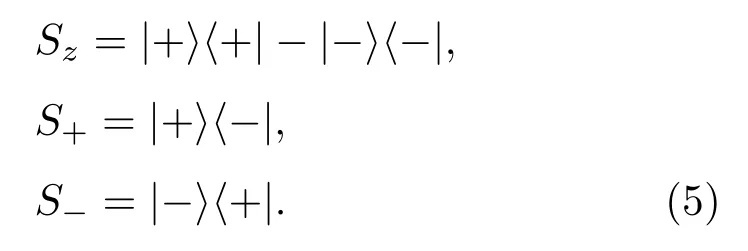
由缀饰态基|+〉,|−〉和|e〉,|g〉之间的关系可得

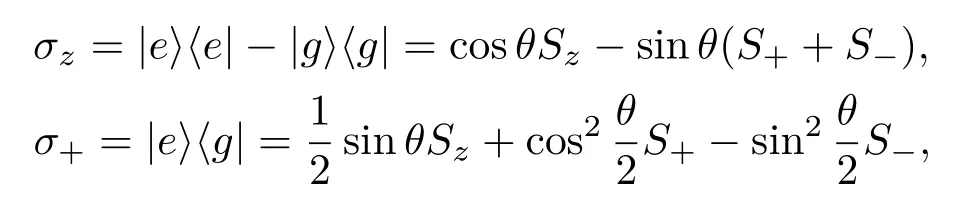
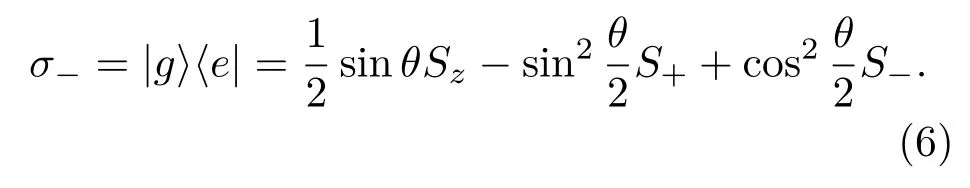
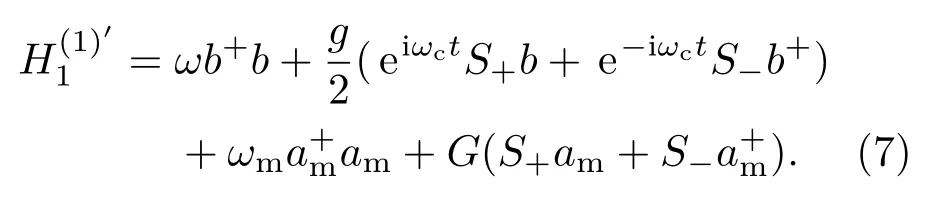
则系统在缀饰态表象下的哈密顿量为

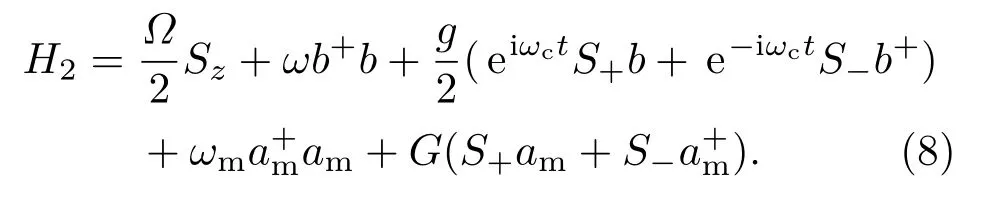
引入幺正操作U2=exp(iωcSzt/2),系统哈密顿量(8)式变为

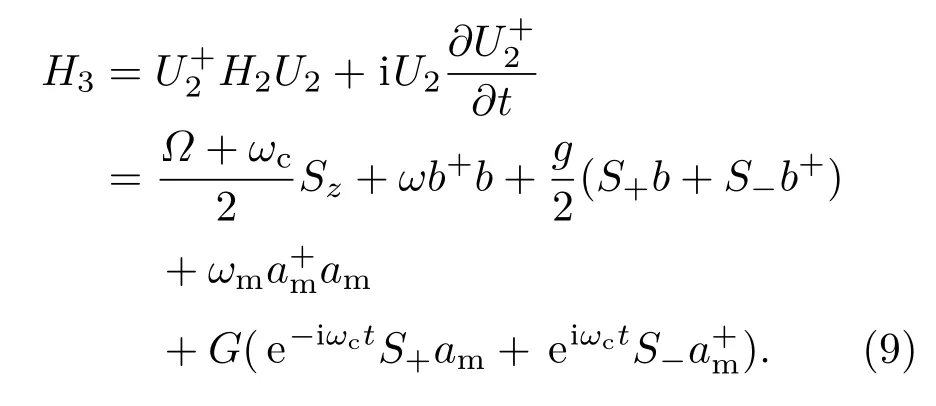
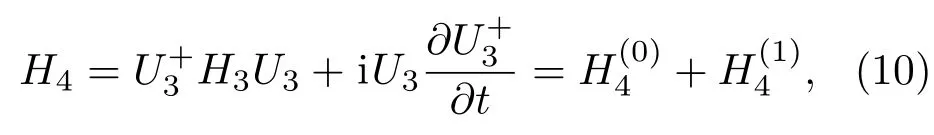
其中

本文主要研究NV色心与机械振子、腔场之间的相互作用,则考虑系统哈密顿量的相互作用部分,在相互作用绘景下,令U4=exp(−iH(0)4t),可得系统相互作用绘景下的哈密顿量为

其中Δ1=Ω+ωc− ω,Δ2=Ω − ωm.考虑特殊情况Δ1=0,Δ2=0,金刚石NV色心初始处于cosθ1|+〉+sinθ1|−〉,机械振子处于基态|0m〉,腔场处于单光子态|1f〉,则系统初态为

在哈密顿量(12)式作用下,系统任意时刻的态矢量为

求解薛定谔方程,可得

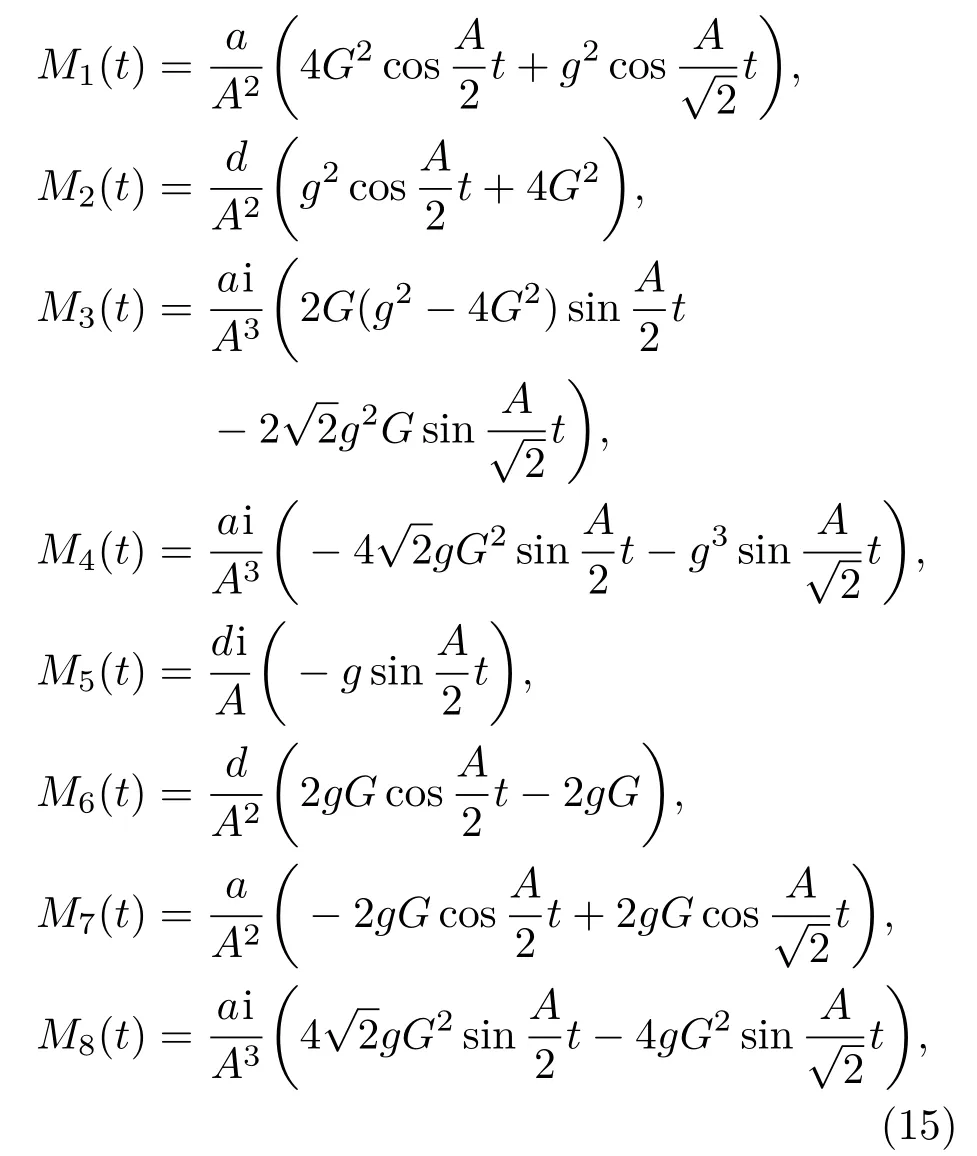
金刚石机械振子的振动模式可以处理成声子振动模,研究声子场的压缩,引入正交算符

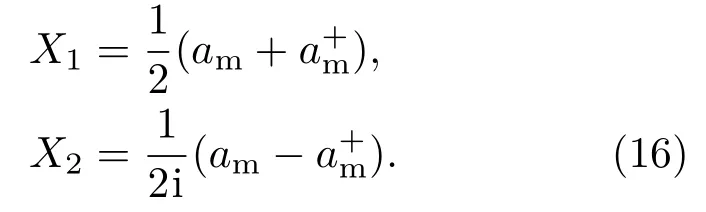
根据方差的定义

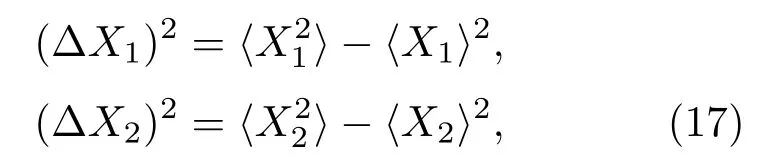
其中

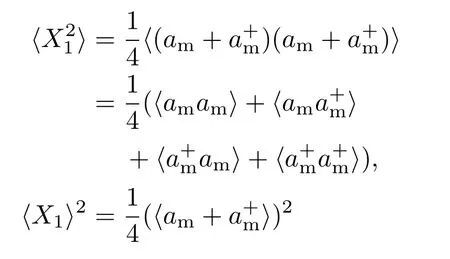
由任意时刻态矢量(14)式,可以得到金刚石机械振子的约化密度矩阵为

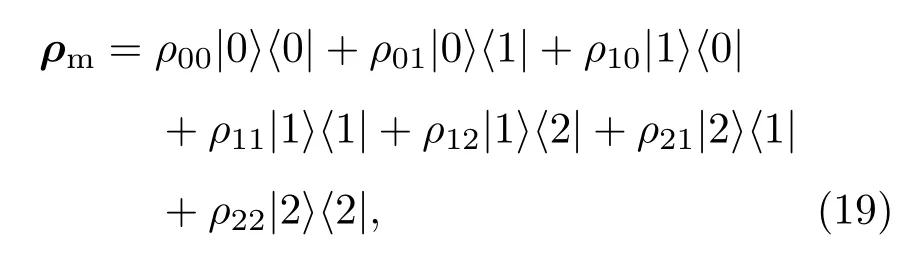
其中

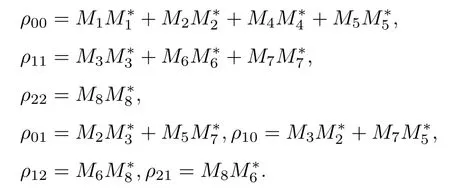
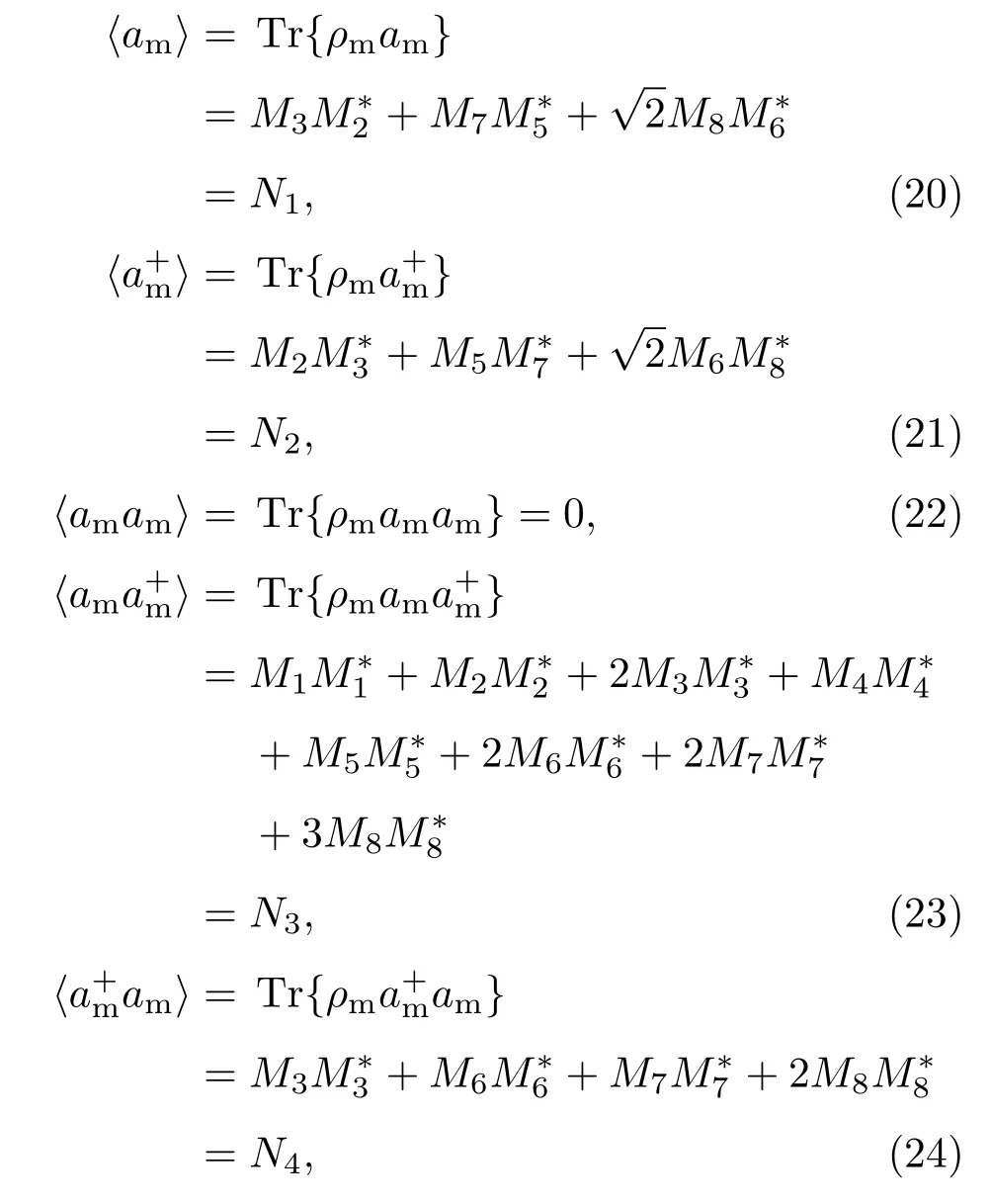
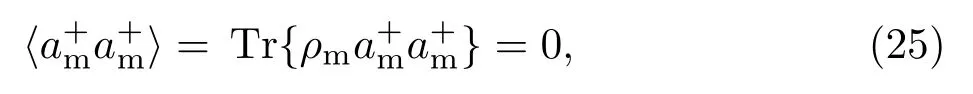
所以

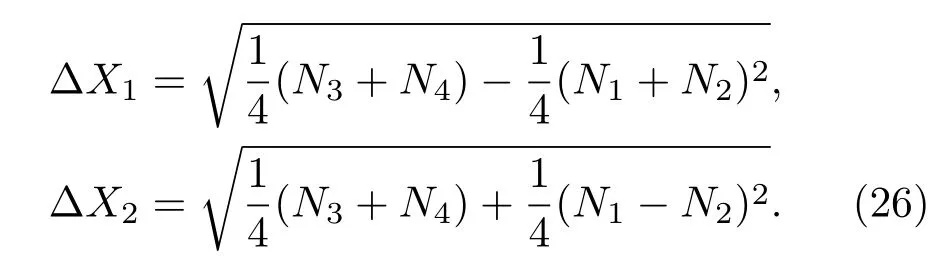
当声子场处于压缩态时,其中一个正交算符的量子涨落小于1/2,减小了声子场某一部分的量子起伏,使测量的精确度提高,由此压缩态在精密测量、引力波探测、光通信、量子信息处理等方面具有重要应用.

为了更好地阐明金刚石机械振子方差压缩的物理机制和原因,给出机械振子的相干性的定义和计算表达式为[19,20]

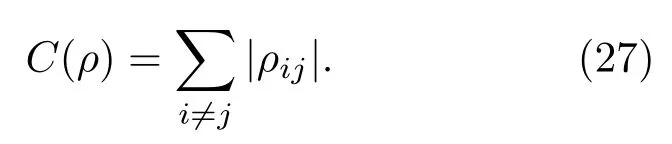
由(19)和(27)式可得机械振子的相干性为

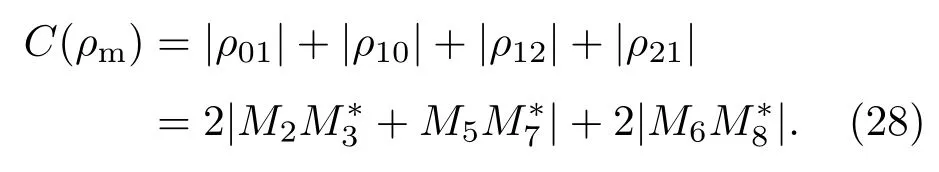
利用以上结果讨论金刚石NV色心初态和NV色心与机械振子耦合强度对声子场方差压缩影响.

3 结果与讨论

图2展示了声子场方差压缩因子ΔX2和相干性随时间的动力学演化特性,图中实线和虚线分别对应声子场方差压缩因子ΔX2和相干性演化规律,其中金刚石NV色心和腔场耦合系数g=1,θ1=π/3,金刚石NV色心和机械振子耦合强度G=0.1,机械振子相干性整体向上平移了0.3数值,由图2可以看出,声子场方差压缩因子ΔX2和相干性随时间的演化呈现振荡行为,t=0初始时刻,声子场方差压缩因子ΔX2为0.5,机械振子相干性为零,不存在压缩,随着金刚石NV色心和机械振子以及腔场的相互作用进行,金刚石NV色心和机械振子以及腔场之间信息和能量不断地交换和转移,声子场方差压缩因子ΔX2小于0.5,声子场出现压缩,此时相干性C大于零呈现相干性,机械振子出现非经典性,当相互作用演化到t≈24时,声子场方差压缩因子ΔX2呈现最大压缩振幅,此时出现最大方差压缩,其物理机制为此时机械振子约化密度矩阵具有最大相干性(由图2中虚线可知),机械振子非经典性越强,方差压缩越大.

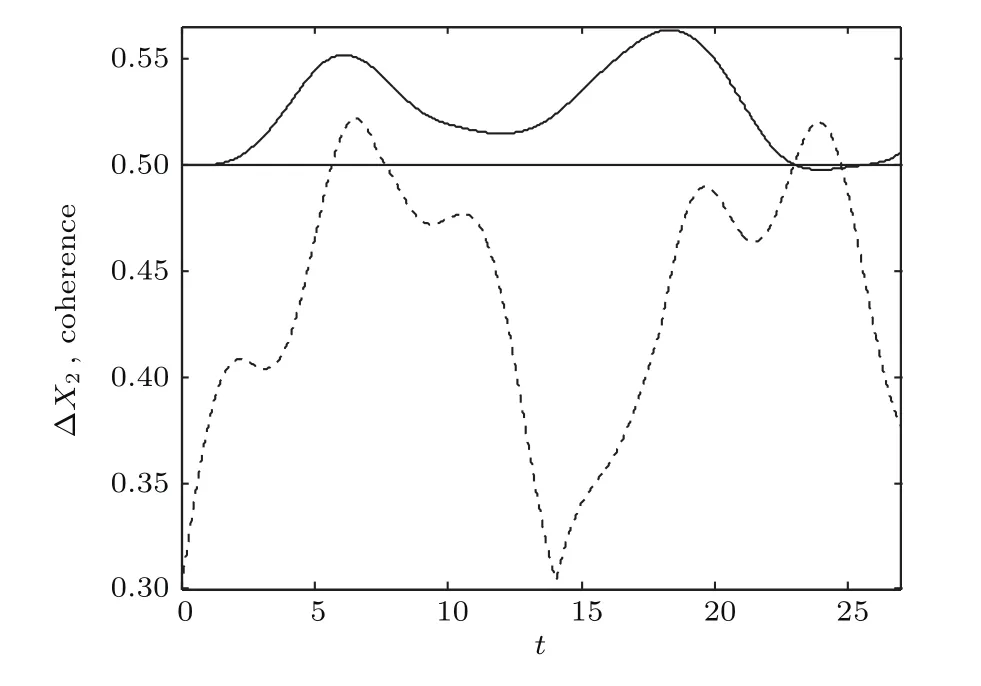
图2 声子场方差压缩因子ΔX2和相干性随时间的演化(参数g=1,θ1= π/3,G=0.1)Fig.2.The time evolution of the quadrature squeezing of the phonon field ΔX2and coherence.The parameters are g=1,θ1= π/3,G=0.1.

图3给出了声子场方差压缩因子ΔX1和ΔX2随时间的演化规律,图3(a)和图3(b)分别对应声子场方差压缩因子ΔX1和ΔX2的演化特性,其中参数g=1,θ1=0,G=0.1.由(15)式可知当θ1=0导致M2(t)=M5(t)=M6(t)=0,从而N1=N2=0,此时由(26)式可以看到声子场方差压缩因子ΔX1和ΔX2随时间具有相同的演化规律.由图3(a)和图3(b)中可以看出,声子场方差压缩因子ΔX1和ΔX2随时间演化取值都大于等于0.5,即声子场在正交算符X1和X2方向上都不存在方差压缩,不存在非经典性,主要原因为此时机械振子约化密度矩阵不存在相干性,机械振子处于混态ρm=ρ00|0〉〈0|+ρ11|1〉〈1|+ρ22|2〉〈2|,此时机械振子不存在非经典特性,X1和X2方向不存在方差压缩.

由于可以通过控制外加经典场实现金刚石NV色心初始态的调控,图4给出了声子场方差压缩因子ΔX2随时间的演化动力学特性,图中实线和虚线分别对应金刚石NV色心不同的初态θ1=π/3和θ1=π/3.5,其他参数与图2相同.由图中实线可知,声子场方差压缩因子ΔX2初始时不存在方差压缩,随着金刚石NV色心和机械振子以及腔场的相互作用进行,声子场方差压缩因子ΔX2小于0.5,声子场出现压缩,由图4中插图可知当相互作用演化到t≈24时,此时出现最大方差压缩,对比图3中实现和虚线可以看到,随着θ1的减小,声子场方差压缩越来越小,压缩时间越来越短,由此结论通过调控金刚石NV色心初态,可以制备压缩时间长,压缩幅度大的声子场压缩态,实现对机械振子方差压缩非经典特性的操控,理论上提供了一种调控声子场方差压缩的方式.

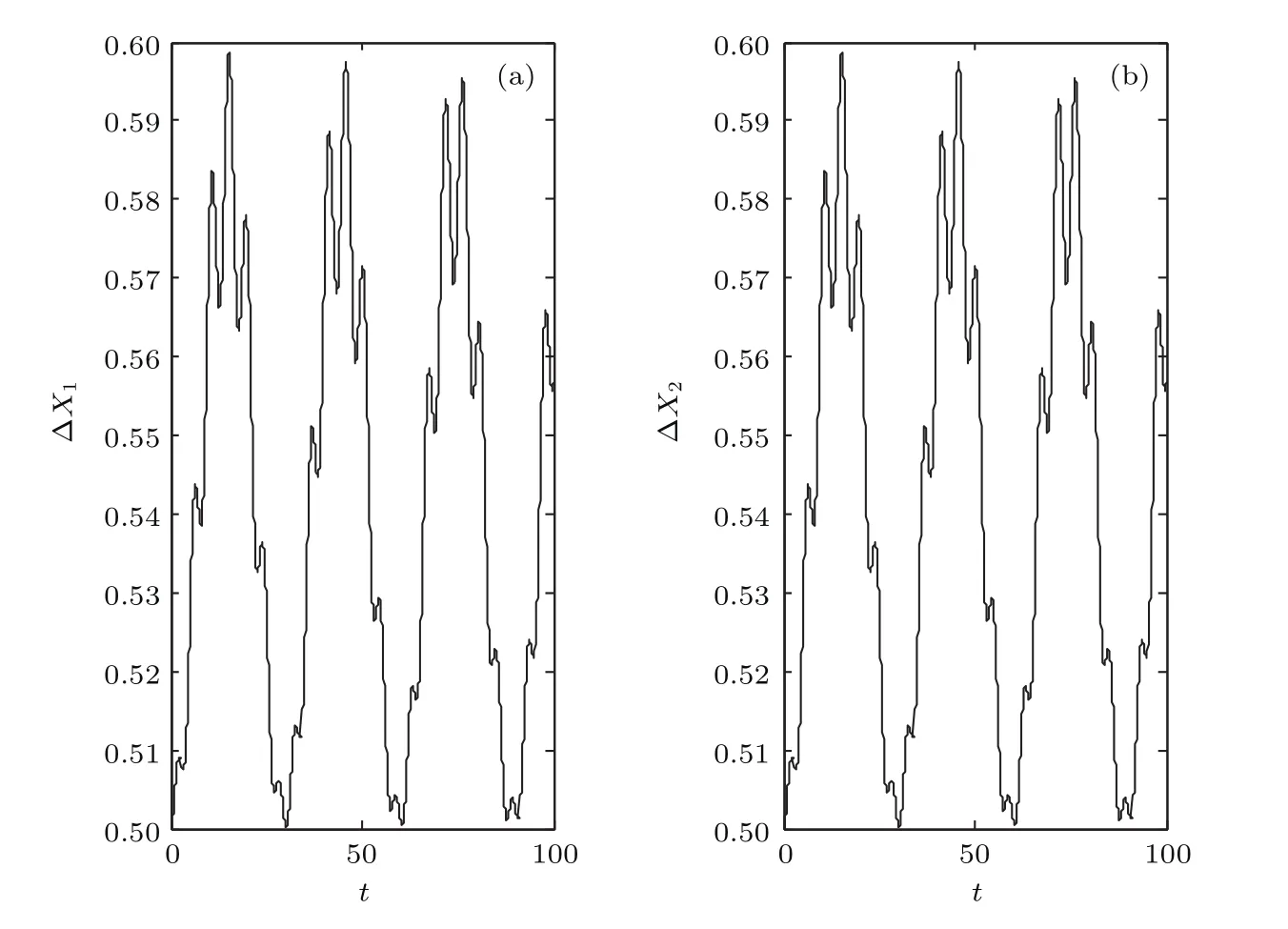
图3 声子场方差压缩因子ΔX1和ΔX2随时间的演化(参数g=1,θ1=0,G=0.1)Fig.3.The time evolution of the quadrature squeezing of the phonon field ΔX1and ΔX2.The parameters are g=1,θ1=0,G=0.1.

为了探讨金刚石NV色心与机械振子耦合强度对系统声子场方差压缩的影响,图5给出了金刚石NV色心与机械振子耦合强度取不同值时声子场方差压缩因子ΔX2随时间的演化行为,图中实线和虚线分别对应金刚石NV色心与机械振子耦合强度G=0.05和G=0.1,其他参数与图2相同.由图5可以看到,金刚石NV色心与机械振子耦合强度影响声子场方差压缩因子ΔX2的振荡幅度以及压缩大小.对比插图中的实线和虚线可知,金刚石NV色心与机械振子耦合强度越大,正交算符X2上涨落振荡的幅度越大,声子场方差压缩幅度越大,机械振子方差压缩非经典特性越强.由金刚石NV色心与机械振子的耦合系数表达式G=gsµBGma0/ħ可知,实验上可以通过调控磁场梯度Gm实现金刚石NV色心与机械振子耦合强度的控制,从而实现对机械振子方差压缩非经典特性的操控.

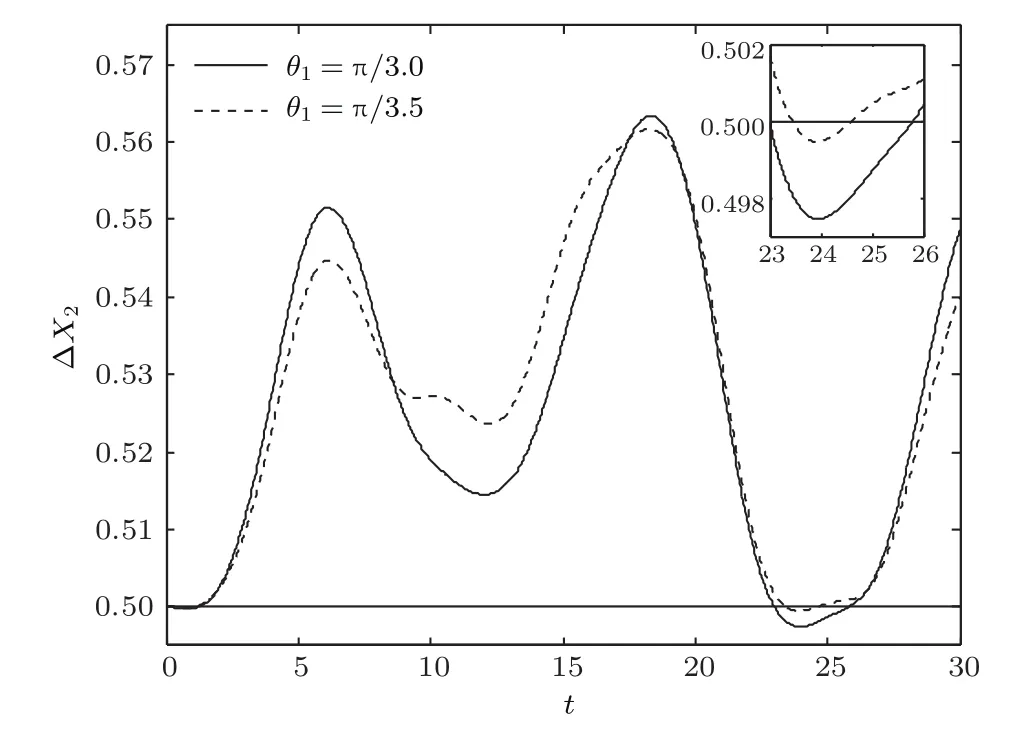
图4 声子场方差压缩因子ΔX2随时间的演化(实线和虚线分别对应θ1=π/3和θ1=π/3.5,其他参数与图2相同)Fig.4.The time evolution of the quadrature squeezing of the phonon field ΔX2.The solid line and the dashed line correspond to θ1= π/3, θ1= π/3.5,respectively.The other parameters are the same as Fig.2.

考虑耗散对系统声子场方差压缩的影响,系统的主方程为

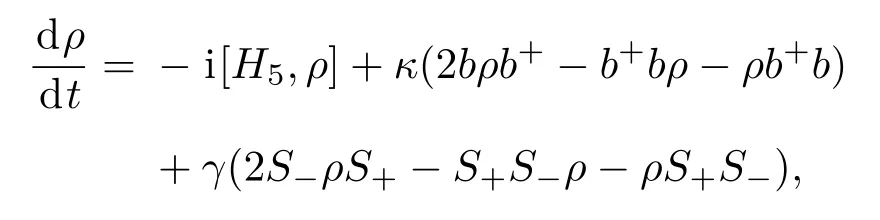
κ和γ分别为腔场衰减率和NV色心自发辐射衰减率.通过数值求解主方程,图6给出了系统存在腔场衰减和NV色心的自发辐射对机械振子方差压缩的影响,图中实线、虚线和点虚线分别对应参数κ=γ=0,κ=γ=0.001和κ=γ=0.005.对比插图中的实线和虚线可以看到:考虑系统的腔场衰减和NV色心自发辐射耗散时,由于存在能量耗散过程,声子场方差压缩幅度越来越小,压缩时间越来越短,机械振子方差压缩非经典特性越来越弱;随着耗散强度的继续增大,由插图中的点虚线(对应参数κ=γ=0.005)发现,声子场方差压缩效应消失,耗散破坏了压缩效应.

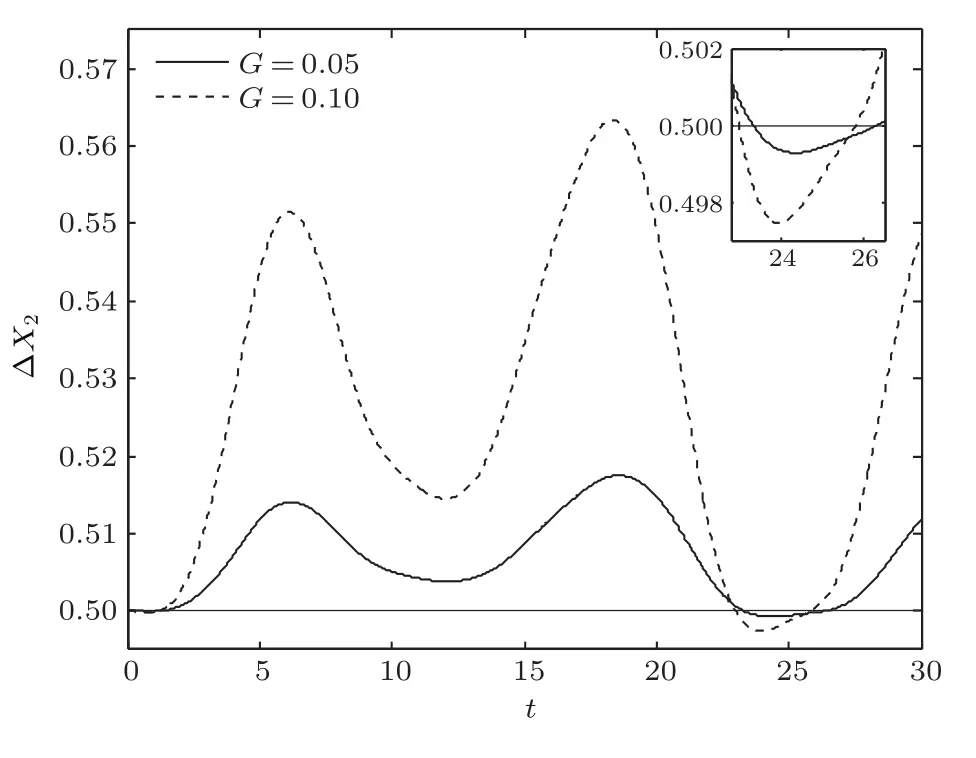
图5 声子场方差压缩因子ΔX2随时间的演化(实线和虚线分别对应G=0.05和G=0.1,其他参数与图2相同)Fig.5.The time evolution of the quadrature squeezing of the phonon field ΔX2.The solid line and the dashed line correspond to G=0.05,G=0.1,respectively.The other parameters are the same as Fig.2.

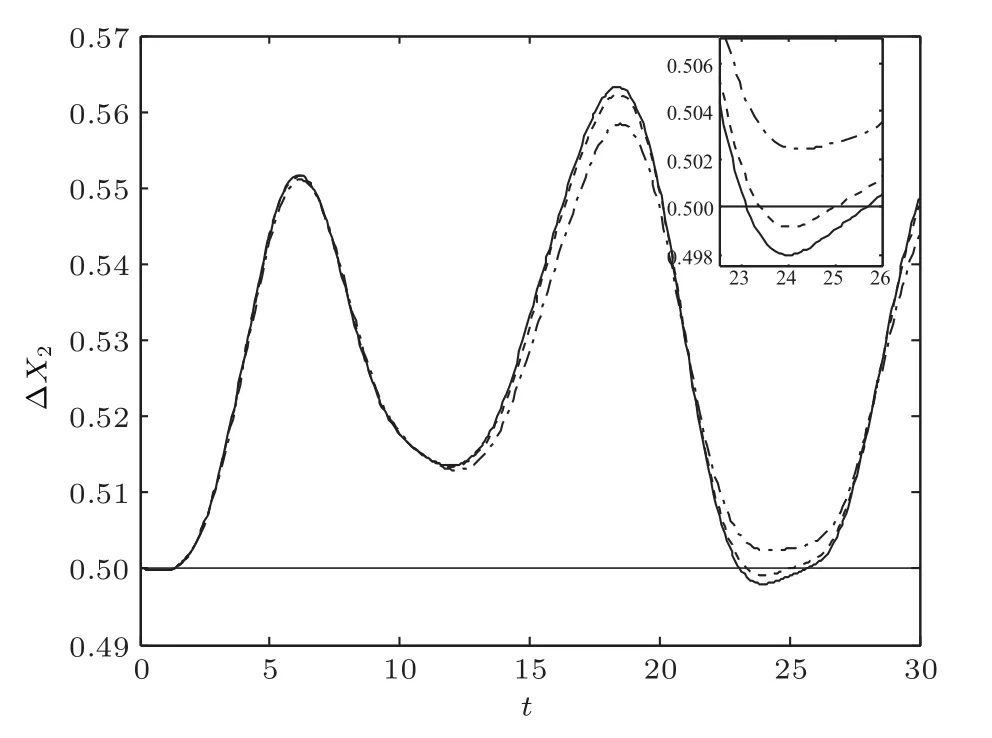
图6 声子场方差压缩因子ΔX2随时间的演化(实线、虚线和点虚线分别对应κ=γ=0,κ=γ=0.001和κ=γ=0.005,其他参数与图2相同)Fig.6.The time evolution of the quadrature squeezing of the phonon field ΔX2.The solid line,dashed line and dotted-dashed line correspond to κ = γ =0,κ=γ=0.001 and κ=γ=0.005,respectively.The other parameters are the same as Fig.2.

这里简单地给出该方案在实验上实现的可行性.文献[21,22]利用光镊技术在液体中实现了内含NV色心的纳米金刚石的囚禁,Neukirch等[23]在实验上实现了内含NV色心的纳米金刚石在自由空间中的光学囚禁,文献[24]利用相似的技术实验上也实现了纳米粒子在真空中的囚禁以及质心运动的探测.McCutcheon和Loncar[25]设计和分析了NV色心放在光子晶体微腔中心或腔表面位置均能实现NV色心与腔场的强耦合方案,随后文献[26]实验上实现了单个NV色心与光子晶体谐振腔的确定性耦合.文献[27]研究了两能级发射器与腔场耦合强度是发射器与机械振子耦合强度的20倍时系统中量子关联特性,同时在NV色心下面放置一个磁针,可以产生很强的梯度磁场[28],实现NV色心电子自旋与纳米金刚石振动的耦合,控制磁场梯度可以很方便地实现金刚石NV色心与机械振子的耦合强度大小的操控.因此,本文研究的金刚石NV色心同时耦合腔场和机械振子系统中声子场的方差压缩系统具备实现的可行性.

4 结 论

本文充分利用金刚石NV色心在室温下具有毫秒量级的长相干时间以及容易被微波操控等优势,研究了驱动金刚石NV色心同时耦合腔场和机械振子系统中声子场的方差压缩动力学特性,引入机械振子的相干性阐明了声子场方差压缩的物理机制,讨论了金刚石NV色心初态和NV色心与机械振子耦合强度对声子场方差压缩的影响,结果发现控制和操纵系统参数可以制备压缩时间长、压缩幅度大的声子场压缩态,并且通过调控NV色心初态以及磁场梯度可以实现对机械振子方差压缩非经典特性的操控,从而在理论上提供了一种调控声子场方差压缩的方式.本文的研究结果将在量子信息处理以及精密测量等研究领域具有重要的意义和应用前景.

感谢清华大学交叉信息研究院助理研究员尹璋琦博士在本文修改过程中提供的有益讨论和帮助.

[1]Carr D W,Evoy S,Sekaric L,Craighead H G,Parpia J M 1999Appl.Phys.Lett.75 920

[2]Blick R H,Roukes M L,Wegscheider W,Bichler M 1998Phys.B:Condensed Matter249 784

[3]Caves C M,Thorne K S,Drever R W P,Sandberg V D,Zimmermann M 1980Rev.Mod.Phys.52 341

[4]Sekaric L,Parpia J M,Craighead H G,Feygelson T,Houston B H,Butler J E 2002Appl.Phys.Lett.81 4455

[5]Xiang Z L,Ashhab S,You J Q,Nori F 2013Rev.Mod.Phys.85 623

[6]Doherty M W,Manson N B,Delaney P,Jelezko F,Wrachtrup J,Hollenberg L C L 2013Phys.Rep.528 1

[7]Yin Z,Li T,Zhang X,Duan L M 2013Phys.Rev.A88 033614

[8]Zhao N,Yin Z Q 2014Phys.Rev.A90 042118

[9]Dolde F,Fedder H,Doherty M W,Nöbauer T,Rempp F,Balasubramanian G 2011Nat.Phys.7 459

[10]Toyli D M,de las Casas C F,Christle D J,Dobrovitski V V,Awschalom D D 2013Proc.Natl.Acad.Sci.USA110 8417

[11]Kolkowitz S,Jayich A C,Unterreithmeier Q P,Bennett S D,Rabl P,Harris J G,Lukin M D 2012Science335 1603

[12]Ovartchaiyapong P,Lee K W,Myers B A,Jayich A C 2011Nat.Commun.5 4429

[13]Li P B,Xiang Z L,Rabl P,Nori F 2016Phys.Rev.Lett.117 015502

[14]Muschik C A,Moulieras S,Bachtold A,Koppens F H,Lewenstein M,Chang D E 2014Phys.Rev.Lett.112 223601

[15]Liu B Y,Cui W,Dai H Y,Chen X,Zhang M 2017Chin.Phys.B26 090303

[16]Liu B Y,Dai H Y,Chen X,Zhang M 2015Eur.Phys.J.D69 104

[17]Rabl P,Cappellaro P,Dutt M V G,Jiang L,Maze J R,Lukin M D 2009Phys.Rev.B79 041302

[18]Liu Y X,Sun C P,Nori F 2006Phys.Rev.A74 052321

[19]Walls D F,Milburn G J,Garrison J C 1994Quantum Optics(Berlin:Springer-Verlag)pp297–303

[20]Yu C S,Song H S 2009Phys.Rev.A80 022324

[21]Horowitz V R,Alemán B J,Christle D J,Cleland A N,Awschalom D D 2012Proc.Natl.Acad.Sci.USA109 13493

[22]Geiselmann M,Juan M L,Renger J,Say J M,Brown L J,de Abajo F J,Koppens F,Quidant R 2013Nat.Nanotechnol.8 175

[23]Neukirch L P,Gieseler J,Quidant R,Novotny L,Nick V A 2013Opt.Lett.38 2976

[24]Gieseler J,Deutsch B M,Quidant R,Novotny L 2012Phys.Rev.Lett.109 103603

[25]Mccutcheon M W,Loncar M 2008Opt.Express16 19136

[26]Englund D,Shields B,Rivoire K,Hatami F,Vučković J,Park H,Lukin M D 2010Nano Lett.10 3922

[27]Restrepo J,Favero I,Ciuti C 2017Phys.Rev.A95 023832

[28]Mamin H J,Poggio M,Degen C L,Rugar D 2007Nat.Nanotechnol.2 301