基于阻抗控制的机器人砂带打磨的建模与仿真

，，，，

(浙江工业大学 信息工程学院，浙江 杭州 310023)

随着现代机械加工的不断发展，使用机器人进行打磨及抛光代替人工作业实现自动化生产是当下的一个研究热点[1].机器人砂带打磨[2-4]是通过机器人末端夹具夹持着工件，根据预先规划好的打磨轨迹，在砂带机上进行打磨操作，整个作业可分为两个子任务：一是在自由空间对打磨轨迹的跟踪；二是在接触空间对打磨接触力的控制，以免因接触力过大而损坏工件又同时保证了打磨质量.近年来，许多学者在机器人砂带打磨领域做了大量的研究工作，洪云飞等[5]开发了一种六自由度机器人砂带打磨系统，该系统利用激光坐标系对工具和工件坐标系作精确的标定，通过离线编程软件规划打磨轨迹，并在打磨机上利用弹簧、比例阀组成力反馈补偿器控制接触力稳定，提高了打磨质量.齐立哲等[6]提出了机器人应用系统的“作业精度”的概念，描述作业点的实际坐标系与标定坐标系的偏差，推导出打磨过程的作业精度模型，以此来设计误差测量工具及补偿方法，提高了工业机器人砂带打磨系统的整体性能.针对工件的变形以及刚度的时变，崔一辉等[7]对打磨机采用浮动横梁技术，保证砂带传递恒定打磨力，测量工件形状，并与理想模型作比较得到期望打磨力，通过力反馈控制后应用于工件打磨.另外，王伟等[8]对砂带打磨机器人的灵活性进行了分析和优化.以上学者对机器人砂带打磨轨迹规划、跟踪和精度控制以及对接触力的补偿做了大量的研究，有效地提高了打磨质量.但是针对机器人砂带打磨的主动力控制[9]研究较少.目前，机器人主动力控制的方法主要是力/位混合控制[10]和阻抗控制[11].力/位混合控制方法在机器人打磨中得到了一定的应用[12]，该方法虽然能够直接控制接触力和位置，但在自由空间与接触空间切换时，会因接触力过大而损坏工件.机器人阻抗控制优于力/位混合控制的特点是不需要切换控制模式，它不是直接地控制接触力或位置，而是通过建立一个用户设定的接触力与位置之间期望的动态关系适应机器人从自由空间到接触空间两种状态下的统一的控制策略以实现机器人与环境间的力控制.而砂带打磨过程中最重要的是控制接触力的恒定，因此基于力跟踪的阻抗控制方案是解决机器人砂带打磨的一种理想方案.Seraji等[13]提出了直接和间接两种自适应力跟踪阻抗控制方法，两种方法在环境参数未知的情况下都具有较好的力跟踪效果，但是由于过多的自适应增益参数的调节使其不利于实际应用.为了便于实际应用，Jung等[14]提出了在未知环境下的机器人力跟踪阻抗控制方法，该方法是根据力反馈误差设计简单的自适应律，只需选取合适的自适应增益使得在环境参数变化的情况下也能表现出很好的力跟踪效果，并且不依赖于机器人动力学模型.因此该方法对机器人砂带打磨系统设计具有一定的参考价值.

笔者针对机器人打磨水龙头过程，基于力跟踪阻抗控制方法建立了一个机器人砂带打磨样机系统.首先，通过分析砂带打磨过程的特点，根据Hertz弹性接触理论建立了连续接触力模型.然后，为了补偿打磨过程中砂带的接触形变量，设计了一种具有自适应补偿的力跟踪阻抗控制器.并且考虑砂带的柔性易形变以及刚柔耦合的接触特性，在Adams中基于模态中性文件法创建砂带柔性体的基础上对机器人砂带打磨过程进行机械系统建模.最后，通过设计Adams和Matlab的接口模块，搭建机器人砂带打磨实验联合仿真平台，对机器人砂带打磨过程的力跟踪阻抗控制进行仿真实验，结果表明该样机具有较好的力跟踪性能.

1 砂带打磨的接触力分析

采用砂带机作为工具固定在地面，机器人通过夹具夹持着水龙头在砂带上进行打磨的工作方式.整个机器人砂带打磨系统如图1(a)所示，主要由六自由度机器人、力传感器、打磨设备和机器人控制系统等组成机器人砂带打磨系统以实现打磨任务.

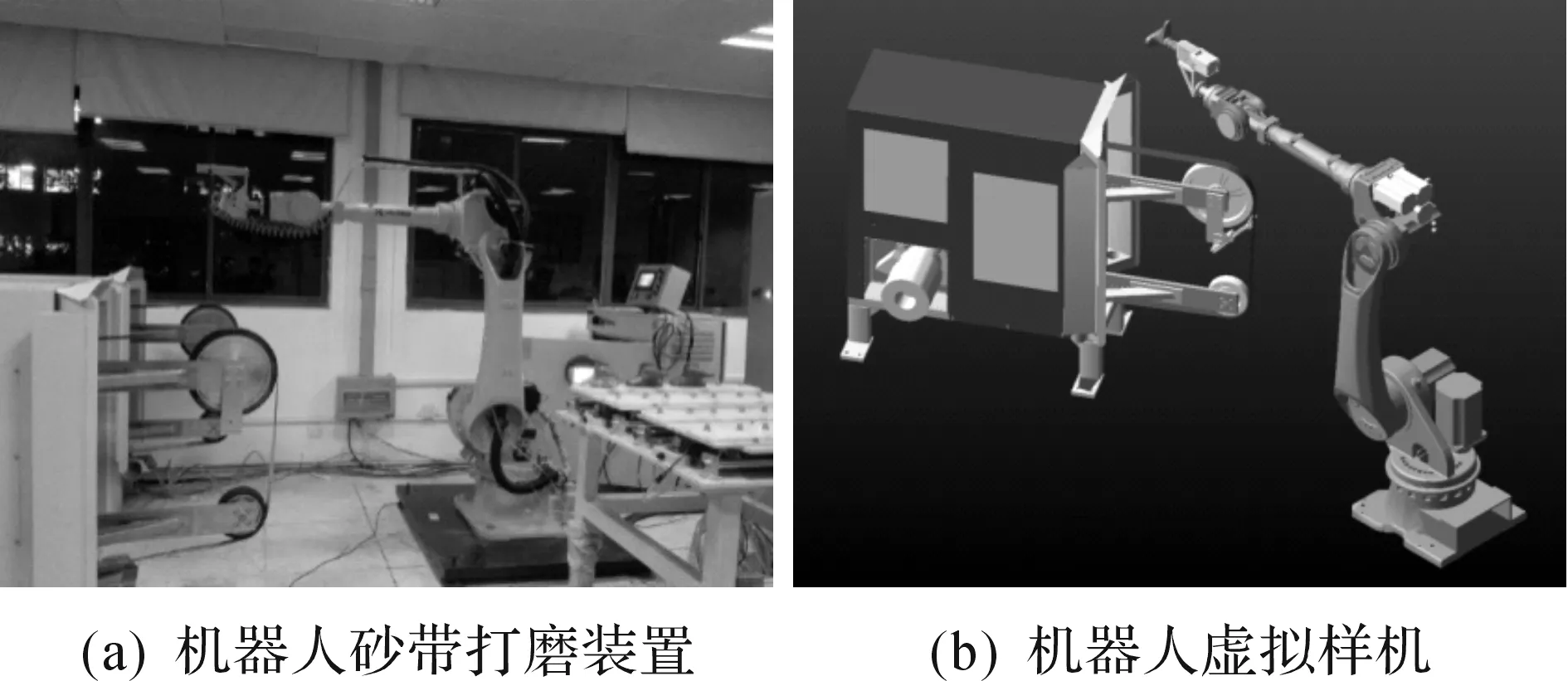
图1 机器人砂带打磨系统Fig.1 Robot belt grinding system

在打磨过程中，机器人夹持着水龙头毛坯以一定的压力持续接触砂带，砂带上的磨粒与工件产生挤压作用，并伴随着较小的塑性变形而产生接触力，因此需要建立连续接触力模型.当水龙头与接触轮接触时，打磨接触力Fe分解为由垂直于工件表面的法向接触力Fn、沿与砂带线速度方向的切向接触力Ft和轴向接触力Fa组成.轴向接触力Fa一般较小，可以忽略不计，接触面上产生的打磨力为

Fe=Fn+Ft

(1)

根据砂带打磨的特点以及Hertz弹性接触理论[15]，引入弹簧描述砂带对形变的抵抗，引入阻尼描述接触过程的能量损失，与砂带接触的打磨段为多点接触，假设为圆弧面且包含N个接触点，连续接触力模型为

(2)

式中：δ=X-Xe为接触形变量，Xe为环境位置，X

在机器人的砂带线速度恒定时，法向接触力大小是影响材料去除量和加工质量的重要因素，与工件之间接触形变量有关；而切向接触力影响砂带的磨损.因此，可通过控制砂带打磨的法向接触力提高砂带打磨质量.

2 力跟踪阻抗控制器设计

如前述，砂带打磨最重要的是控制法向接触力，因此，需要建立水龙头表面与砂带的刚柔耦合关系.分析与砂带接触时力的闭环动态关系，如图2所示.

建立接触力与期望力的传递函数为

(3)

式中：环境阻抗模型Ze(s)=Be+Ke/s；机器人阻抗模型Zd(s)=Mds+Bd+Kd/s，其中Md，Bd，Kd分别为正定对角的期望惯性、阻尼和刚度矩阵.

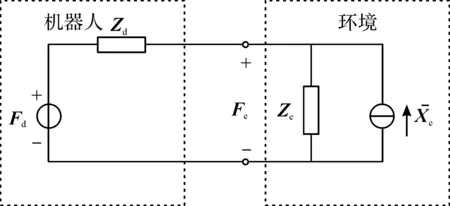
图2 接触力控制模型Fig.2 Contact force controlled loop

借鉴文献[14]，在时域中力跟踪期望阻抗函数模型为

(4)

式中：E=Xr-X，Xr为参考轨迹位置；Fd为期望接触力.

由式(3)得接触力的稳态误差为

(5)

由式(5)可知：为了保证力跟踪误差为0，通过设置刚度增益Kd为0，对任意的Ke>0都能满足理想稳定状态.

机器人砂带打磨的工作空间分为f维力控制子空间和p维位置控制子空间，设计阻抗控制器分为两个阶段，一是在自由空间机器人夹持水龙头接触砂带表面的位置跟踪阻抗控制；二是在接触空间机器人进行砂带打磨的力跟踪阻抗控制.

在自由空间中，不与砂带接触，外力Fe=0，参考轨迹Xr为规划的期望轨迹Xd，由式(4)得自由空间运动的阻抗函数为

(6)

在接触空间中，参考位置Xr为砂带位置Xe，在环境刚度未知的情况下，据前述，力控制方向上的刚度Kdf=0，根据式(4)取单分量方向简化分析，则接触空间的阻抗模型为

1)位控制方向：

(7)

2)力控制方向：

(8)

式中：mdp,bdp,kdp,ep,fdp,mdf,bdf,ef,fef,fdf分别为第p维位置控制方向上和第f维力控制方向上的期望惯性、期望阻尼、期望刚度、位置偏差和期望接触力.

为了使接触力响应有较小的阻尼振荡，阻抗参数需满足

(9)

由于砂带的柔性导致接触位置变化，实际砂带的接触位置很难精确测量得到，因此，式(9)的期望阻抗模型是无法保证Fef=Fdf.

为了减小接触变形量引起的力误差，在式(8)的速度项增加自调整项φ(t)，补偿砂带位置变化，得到具有自适应补偿的力跟踪阻抗模型为

(10)

其中

φ(t)=φ(t-λ)+η[fdf(t-λ)-fef(t-λ)]/bdf

(11)

式中：λ为采样周期；η为补偿系数.

为了满足式(10)的稳定性，将式(11)进行拉式变换，由位移定理[16]得

(12)

由于λ很小，将式(12)的e-λs按泰勒级数展开，可取前两项即e-λs≈1-λs，再代入式(10)得力误差与位置偏差的传递函数，其特征方程为

mdfλs3+λ(bdf+bef-ηbef)s2+(λkef-ηλkef+

ηbef)s+ηkef=0

(13)

由劳斯稳定性判据得式(13)的补偿系数需满足

mdfkef)η-λkef(bdf+bef)<0

(14)

(15)

JTFe(t-λ)

(16)

(17)

(18)

由式(15～18)得控制律为

(19)

图3 机器人砂带打磨力跟踪阻抗控制结构图Fig.3 Force tracking impedance control scheme of the robotic belt grinding

3 机器人砂带打磨虚拟样机建模与控制系统仿真

考虑砂带的柔性易形变以及刚柔耦合接触特性使得打磨接触过程的动力学变得相当复杂，因此需要对机器人砂带打磨系统的整个过程进行机械建模，利用Adams可对机器人进行静力学、运动学和动力学分析[19]使得样机更接近于实际物理模型[20]，机器人砂带打磨系统的具体仿真实现如图4所示.

3.1 虚拟样机的建模过程

首先根据汇博ER50-C10机器人的D-H参数如表1所示，利用Matlab的Robotics Toolbox创建机器人连杆模型，确定机器人零位位姿.然后在Solidworks建立六轴机器人的三维几何模型并调整到相应的零位位姿.最后利用模型数据交换接口格式Parasolid保存扩展名为*.X_T的文件，导入到Adams，如图5所示.

图4 机器人砂带打磨系统的实现过程Fig.4 The implementation process of the robot belt grindingsystem

关节iθi/(°)di-1/mmai-1/mmαi-1/(°)范围/(°)1056321790±18029009000-130～7030015790-72～22041801017090±36051800090±1206019500±360

图5 机器人虚拟样机的建模过程Fig.5 Modeling process of the robotic virtual prototype

为了使机器人的虚拟样机具有与实际机器人相近的物理特性，处理过程如下：1) 赋予机器人虚拟样机一定的材料等重要属性；2) 在每个转动关节添加旋转副，其他无相对运动的构件则添加固定约束或必要的布尔操作来简化样机；3) 给样机添加单分量力矩以及摩擦等重要载荷信息，完成机器人虚拟样机的建立.在此基础上，根据打磨要求，将打磨设备如打磨工件、砂带机等以同样的方式导入到Adams中，搭建成简易的机器人砂带打磨样机系统.考虑砂带的弹性，以及提高仿真的精度，在样机中引入柔性体，将砂带进行柔性化处理，根据材料信息以及设置砂带的模态阶数为10，计算得到模态中性文件(MNF)，如图6所示.从图6中可以得到计算柔性体过程中生成的节点数量和网格数量.将MNF文件导入并替换刚性砂带生成柔性体如图1(b)所示，编辑砂带的模态阻尼比为0.1.根据式(1，2)在Adams中定义水龙头与砂带之间的接触关系为Flex to solid.至此，完成机器人砂带打磨的虚拟样机的建模如图1(b)所示.

图6 MNF文件的计算过程Fig.6 MNF file calculation process

3.2 控制系统仿真平台搭建

为了模拟砂带打磨的实际工况，将Adams中已经建立好的机器人砂带打磨机械系统作为Matlab的一个机械子系统，共同搭建打磨控制系统的仿真平台.首先，利用Adams/Controls模块与控制系统设计软件Matlab进行交互式仿真分析，确定Adams的输入和输出状态变量，其中由Matlab通过控制器输出力矩作为Adams输入变量即机器人的6个关节力矩，通过Adams中的取值函数VARVAL(Torque)读取Matlab输入到Adams中的力矩变量并建立与状态变量的关联；输出变量为打磨接触力、各关节角以及关节角速度，通过相应的测量函数，如AZ(To_Marker，From_Marker)，WZ(To_Marker，From_Marker，About_Marker)等，获取变量值传递给输出状态变量，在Adams与Matlab之间通过状态方程形成一个闭环系统，如图4的虚线框所示.

定义机械系统输入/输出状态变量后，将其导出.利用Adams和Matlab接口命令adams_sys将打磨装置机械子系统导入Matlab.

最后，机器人打磨水龙头自动化程序由图7的离线编程软件ER-RobotStudio仿真环境下生成，考虑到水龙头的几何特殊性，其主要特征为二次曲面相交或者多个曲面拼接而成，曲面上各点的曲率不同，曲率较小的区域，轨迹点稀疏；曲率较大的区域，轨迹点密集，机器人调整相应的姿态进行规划轨迹，生成的轨迹点作为Matlab期望轨迹输入并根据图3在Matlab中搭建联合仿真平台.

图7 机器人砂带打磨过程的离线编程Fig.7 Offline programming of the robotic belt grinding process

3.3 机器人砂带打磨仿真实验

60.5，11.5，5.25，1.88，1.78} kg·mm2，给定期望打磨接触力Fd=[20，0，0，0，0，0]TN,即法向分力Fdn=10 N.

具体的仿真过程如图8所示，同步唤醒Adams进行交互式仿真：在0～1.5 s内机器人从自由空间初始位置夹持着水龙头靠近砂带机直至与砂带接触，根据位置控制律，将关节角和关节角速度传递给控制系统，与此同时，控制器根据期望轨迹传递关节力矩给机械系统，机器人跟踪期望轨迹运动；在1.5～5.0 s内机器人进行打磨操作，法向接触分力响应曲线如图9所示，在自由空间与接触空间过渡瞬间产生较大的接触力，而后在1.5～3.5 s内随着打磨运动自适应迭代补偿快速地调节末端法向接触力稳定在20 N附近，控制在±20%内，在3.5～5.0 s内机器人接触力在20 N附近波动，误差范围小于1 N；在5.0～8.0 s内机器人回到安全位置.图10，11给出关节角和关节角速度变化曲线，由图10，11可知：机器人砂带打磨过程中各关节角和角速度实时变化，实现力跟踪.图9～11的轨迹可辅助实际机器人砂带打磨轨迹规划，对打磨轨迹的优化有一定的实际参考价值.

图8 机器人砂带打磨水龙头过程Fig.8 Roboticbelt grinding process for the tap

图9 打磨过程中法向接触力曲线Fig.9 Contact force curve of grinding process

图10 关节角度曲线Fig.10 Joint angle curves

图11 关节角速度曲线Fig.11 Joint angular velocity curves

4 结 论

考虑砂带打磨过程中的刚柔耦合关系，建立了一种机器人砂带打磨水龙头样机系统，在Adams中建立六自由度机器人砂带打磨系统的虚拟样机，该样机具有与实际模型相近的物理特性，并将其作为Matlab的一个机械子系统.Adams和Matlab联合仿真结果表明了基于力跟踪阻抗控制方法所设计的机器人砂带打磨系统的可行性，能够实现快速的力跟踪，提高了工件的打磨质量，可以作为实际应用的理论依据和参考.在以后的工作中，由于机器人接触过渡的瞬间会产生较大的力，需要对阻抗控制的位置控制到力跟踪阻抗控制的过渡过程的控制性能进行分析以及在实际打磨中的具体实现，考虑到打磨水龙头的复杂曲面对轨迹要求较高，有待在后续的研究中利用迭代的思想优化打磨轨迹来改进.

[1] 金寿松，林新忠，徐泽侠，等.无人化齿轮厂生产布局的研究[J].浙江工业大学学报，2014，42(5):544-548.

[2] 黄云，黄智.砂带磨削的发展及关键技术[J].中国机械工程，2007，18(18)：2263-2267.

[3] 路勇，黄云.砂带磨削磨损性能试验研究[J].机械科学与技术，2014，33(12)：1865-1868.

[4] 黄云，黄智.现代砂带磨削技术及工程应用[M].重庆：重庆大学出版社，2009：81-92.

[5] 洪云飞，李成群，贠超.用于复杂空间曲面加工的机器人磨削系统[J].中国机械工程，2006，8(17):150-152.

[6] 齐立哲，甘中学，贠超，等.机器人砂带磨削系统作业精度分析与误差补偿[J].机器人，2010，32(6):787-791.

[7] 崔一辉，贠超，李成群，等.基于复杂曲面加工的机器人砂带磨削系统的设计及其试验分析[J].中国机械工程，2009，20(10):1144-1147.

[8] 王伟，贠超.砂带磨削机器人的灵活性分析与优化[J].机器人，

2010，32(1):48-54.

[9] VUKOBRATOVIC M， SURDILOVIC D， EKALOY， et al. Dynamics and robust control of robot-environment interaction[M].London: World Scientific Publishing，2009.

[10] RAIBERT M H， CRAIGJ J. Hybrid position/force control of manipulators[J]. Journal of dynamic systems measurement & control，1980，103(2):126-133.

[11] HOGAN N. Impedance control: an approach to manipulator， partⅠ-theory， partⅡ-implementation， partⅢ- application[J]. ASME journal of dynamic systems， measurement and control，1985(1):1-24.

[12] 张庆伟，韩利利，徐方.基于打磨机器人的力/位混合控制策略研究[J].化工自动化及仪表，2012，39(7):52-55.

[13] SERAJI H， COLBAUGH R. Force tracking in impedance control[J]. Internation journal of robotics research，1993，16(1):97-117.

[14] JUNG S， HSIATC，BONITZRG. Force tracking impedance control of robot manipulators unknown environment[J].IEEE transaction on control systems technology,2004，12(3):474-483.

[15] 胡夏夏，宋斌斌，戴小霞，等.基于Hertz接触理论的齿轮接触分析[J].浙江工业大学学报，2016，44(1)：19-22.

[16] 胡寿松.自动控制原理[M].5版.北京:科学出版社，2007：632-644.

[17] JIN M， KANG S H， CHANG P H. Robust compliant motion control of robot with nonlinear friction using time-delay estimation[J]. IEEE transactions on industrial electronics，2008，55(1)：258-269.

[18] BONITZ R G， HSIAT C. Robust internal-force based impedance control for coordinating manipulators-theory and experiments[C]//IEEE International Conference on Robotics and Automation.Minneapolis：IEEE，1996：622-628.

[19] 裘信国，周鑫卓，周见行，等.三支点叉车转向齿轮设计及动力学仿真[J].浙江工业大学学报，2016，44(1)：23-27.

[20] 李增刚.ADAMS入门详解与实例[M].2版.北京:国防工业出版社，2008：133-183.

[21] 王芳，杨振.基于阻抗控制的机器人力控制算法性能分析[J].制造业自动化，2010，32(9):140-142.