高效电磁式振动能量收集装置的设计

，

(1.浙江工业大学 计算机科学与技术学院，浙江 杭州 310023；2.浙江工业大学 信息工程学院，浙江 杭州 310023)

近年来，微传感器和微机电系统被广泛应用于无线传感网络[1]、环境监测[2]、物联网[3]、结构健康监测、植入式医疗检测和汽车胎压监测等社会生活中的各个方面[4].系统使用传统化学电池供能，但是化学电池有寿命短、对环境有污染和需要定期更换成本高等缺点，无法满足实际使用的需求，所以如何为这些器件提供自给能源是系统实用化、商品化的关键问题.自然界中存在不同频率和强度的振动能，众多学者纷纷考虑利用能量收集技术，将环境中的振动能转换成电能为传感器节点供电[5-6].

目前，振动能量收集方式可以分为静电式、压电式和电磁式，其中在振动频率较低，加速度较小时电磁式表现较好[7-9].杜克大学的Mann等提出一种利用磁悬浮力来收集非线性振动产生的能量的方法并进行理论分析，该装置在实际测试情况下最大可以输出2.5 mW的电量[10].安徽大学的王佩红等设计的一款三明治式能量收集器在频率为280.9 Hz的外界振动激励下可以得到125 mW的最大负载电压和13.2 μW的最大负载功率[11].以上设计中，装置均需要永磁体或线圈振动，会损害装置寿命，为解决上述问题提出一种新型方形振子电磁低频振动能量收集装置，采用方形振子在振动轴上振动的方法，平衡了振子的横向吸引力，降低振子运动阻力，永磁体和线圈位置固定提高了装置的工作效率和使用寿命，并且通过对模型的仿真，选择合适的结构参数，优化整个装置设计.

1 结构模型和工作原理

1.1 振动能量分析

直线电磁式振动能量收集装置的理想模型如图1所示.该模型在文献[12-15]中提出：用于分析直线电磁式振动能量收集装置的工作效率以及装置运行过程中的能量损耗.其中质量块等效为装置的振子，x(t)为内部振子的相对装置的位移，u(t)为整个装置相对外部环境的位移，阻尼器为装置中所受到的各种阻力，k为内部弹簧的弹性系数.

图1 直线电磁振动能量收集装置理想工作模型Fig.1 Ideal working model of linear electromagnetic vibration energy collection device

整个装置根据第二牛顿定律可以总结为

mx′′(t)=-kx(t)-bx′(t)-mu′′(t)

(1)

式中：x′(t)，x′′(t)为函数x(t)的一阶二阶导数；u′′(t)为u(t)的二阶导数.能量是通过质量块和装置的相对位移产生的，假设整个装置外部以u(t)=Usin(ωt)运行，则装置内部振子[13]的位移为

(2)

式中φ为装置振动的相位角，即

(3)

则x(t)的稳态响应的振动幅值为

(4)

对单个振动周期内阻尼器位移进行积分可以计算出1 个周期内阻尼器消耗的能量，即转换的能量为

(5)

则系统单位时间内的平均功率[14]为

(6)

1.2 装置实际发电效率分析

直线电磁振动能量收集装置理想工作模型中，阻尼器代表装置中机械能转换电能的器件，整个装置的阻尼能量损耗即为发电量的大小.理想模型中阻尼器主要特征b在运动过程中是个常量，未发生变化.

图2为电磁式方形振子能量收集装置工作时振子的受力分析图，从图2可以知道：在实际运行过程中，振子运动的过程受到电磁力的干扰，产生运动阻力，而且产生的电磁力会把中间振子模块向两边偏移，造成接触模块的摩擦力增加，损耗增大，所以式(6)中得到的最大发电功率是由寄生损耗和产生的电能共同组成.

图2 装置受力分析图Fig.2 Force analysis diagram

根据ω=ωn，式(6)变换成

(7)

假定装置产生功率由转换而来的电能ζe和寄生损耗损失掉的ζl组成，ζ=ζe+ζl，则装置中产生的有效功率[13]为

(8)

(9)

则此时Pe在ζe=ζl时获得最大输出功率为

(10)

从式(10)中可以知道：电磁式振动能量收集系统的收集功率与质量块、系统振动幅值以及寄生损耗相关.系统振动幅值和共振频率越大，装置的能量收集功率也就越大.同样减小装置的寄生损耗，也可以增大系统的能量收集功率.

1.3 电磁式振动能量收集装置的结构

电磁式振动能量收集装置的结构模型如图3所示.该结构包括对称放置的4 片磁轭、放置线圈的铁芯支架、底座、永磁体、方轴、弹簧、方形振子和漆包线线圈.4 片磁轭两两对称分为左右磁轭和前后磁轭，磁轭上磁齿间距与磁齿宽度相同，相邻磁轭上磁齿交错放置，相对磁轭结构完全相同.永磁体为长方体结构，由底座包围，按x=y方向充磁，负方向为N极，正方向为S极.左侧底座为N极，右侧底座为S极.底座与线圈支架相连，线圈支架由上支架、下支架和铁芯组成.振子为方形结构，振子的边长略小于磁轭上磁齿的内边长，形成气隙.结构中间有1 根方形的导轨，振子在导轨上滑动.装置上方有1 个顶盖与导轨相连，用于固定导轨和4 片磁轭，导轨与顶盖均由不导磁材料制成.永磁体采用磁能积、矫顽力和剩磁比较高的稀土材料NdFeB.导磁材料为相对磁导率较高的软磁材料硅钢片.新型电磁式振动能量收集装置主要参数：模型中设定磁轭厚度为3.5 mm，磁轭高度为50 mm，磁齿厚度为1.5 mm，磁齿高度为3 mm，铁芯高度为10 mm，铁芯半径为1.5 mm，振子齿厚度为2.1 mm，振子齿边长为3.9 mm，永磁体长、宽和高分别为6，6，3 mm.

图3 方形振子电磁振动能量收集装置Fig.3 Square vibrator electromagnetic vibration energy collecting device

1.4 能量收集装置的工作原理

随着振子延径向振动，振子与磁齿间发生周性变化，穿过线圈的磁通量也随之发生变化，从而在线圈中产生感应电动势.根据电磁感应定律，线圈中产生的感应电动势表示为

(11)

式中：N为线圈匝数；Ψ为磁链，即穿过N匝线圈的磁通量之和；φ为穿过单匝线圈的磁通量[16].

图4给出了5 种振子的位置，分析振子位置变化对线圈中磁通量的影响.为便于分析，图4中只给出左磁轭和右磁轭与振子的位置关系，前磁轭和后磁轭的磁通量变化与左、右磁轭一致.

图4(a)：振子齿与左磁轭和右磁轭上的磁齿对应，即振子齿中心点与磁齿中心点在同一水平线上.磁力线由磁铁N极发出，经过左铁芯、左磁轭、振子、右磁轭和右铁芯，回到永磁体S极.此时，左、右线圈中磁感应强度为最大，磁通量为最大值.

图4(b)：随振子向上移动，振子齿与左、右磁轭磁齿对应面积逐渐减小，磁感应强度在左、右磁轭上损耗加大，磁力线从磁铁N极出发，经左铁芯、左磁轭、振子、右磁轭和右铁芯回到磁铁S极.此时，左、右线圈中磁感应强度随振子移动逐渐减小.但同时，由于振子的移动，前、后磁轭与振子齿对应面积逐渐加大，磁力线同样会从磁铁N极出发，经后铁芯、后磁轭、振子、前磁轭和前铁芯回到磁铁S极，此时前、后线圈中磁感应强度逐渐增大.

图4(c)：振子齿与左、右磁轭磁齿相互错开，对应面积为0，同时与前、后磁轭磁齿对应面积最大.磁力线经过后铁芯、后磁轭、振子、前磁轭和前铁芯流向磁铁S极.此时，左、右线圈中磁通量为最小值，前、后线圈中磁通量为最大值.

图4(d)：随振子继续移动，振子齿与左、右磁轭磁齿对应面积增大，与前、后磁轭磁齿对应面积逐渐减小，此时磁力线与图4(b)中流动类似.磁力线会同时穿过4 片对应磁轭，当振子齿与磁齿对应面积与位置2中两者对应面积相等时，线圈中磁感应强度也对应相等，穿过线圈的磁通量也相等.

图4(e)：振子齿中心点与磁齿中心点再次回到同一水平线上.左、右线圈中磁感应强度回到最大值，磁通量完成1 个周期变化.

图4 振子与磁轭的5 种位置Fig.4 5 positions of the vibrator and the yoke

2 参数设定与优化

2.1 参数设定

为获得最优装置参数，使用Ansoft Maxwell有限元分析软件对装置进行求解，通过静态仿真对装置的主要结构参数进行优化，并通过动态仿真分析整个模型工作效率.

首先使用Ansoft Maxwell根据1.3 节中的结构参数建立整个模型，之后进行材料设定.设定空气的相对磁导率为默认参数1，永磁体选择剩磁密度为1.3 T，矫顽力为450 kA/m的NdFeB稀土材料.导磁材料选择软磁材料硅钢，其中相对磁导率的设定可根据2.2 节中参数优化结果设定.

完成整个模型的材料设定之后，需要对装置模型进行网格划分.网格划分是将结构模型进行有限元分解，便于Ansoft Maxwell软件进行求解.网格划分的尺寸大小会影响装置模型的仿真结果，尺寸越小精确度越高，同时运算的时间也就越长，仿真中选择0.1 mm的网格划分尺寸.

激励源是进行仿真的关键，直接影响仿真的结果.装置中永磁体是整个模型的唯一激励源，必须设定合适的参数.本装置中根据实际需要设定永磁体为长6 mm，宽6 mm，高3 mm的长方体.

根据优化方向设定合适的求解类型，根据漏磁对装置结构各个参数的影响进行仿真，并依据仿真结果对装置结构进行优化.

2.2 参数优化

磁路与电路不同，目前还没发现磁通不能通过的介质，所以无法将磁通严格地约束在理想的路径中，这就必然导致磁漏.同时，导磁材料的选择，结构尺寸的变化，都会影响铁芯中的磁感应强度，从而影响装置的发电效率.使用Ansoft Maxwell软件对装置做静态仿真，从气隙宽度、相对磁导率和振子齿厚度三个角度定量分析了参数变化对线圈中磁感应强度和边缘效应的影响.

图5(a)是振子与磁轭处于图4(a)时，气隙宽度的变化对铁芯中磁感应强度的影响.静态仿真设置气隙宽度从0.1 mm到1 mm逐渐增大.从图5(a)中可以看到：铁芯中的磁感应强度随着气隙宽度的增大逐渐减小，说明磁损耗越来越严重，气隙宽度为0.1 mm时，磁感应强度为最大.因此，气隙宽度设定为0.1 mm，振子齿的边长为3.9 mm.

气隙是闭合磁路中以空气为介质的路段，但是空气的相对磁导率较低，而且空气本身与周围的环境之间没有边界，气隙较大时，磁路中的磁力线会向外扩散，引起边缘效应.

选择导磁材料考虑的主要因素是相对磁导率，相对磁导率较小时，导磁性能太差，相对磁导率较高时，导磁材料价格昂贵，增加装置成本.图5(b)是相对磁导率对铁芯中磁感应强度的影响.随着相对磁导率的增大，铁芯中磁感应强度不断变大.当相对磁导率大于6 000时，曲线趋于平滑，磁感应强度基本不再变化.因此，装置选择相对磁导率为6 000的导磁材料.

图5(c)是振子齿厚度对铁芯中磁感应强度的影响，即为振子与磁轭磁齿的有效相对面积对铁芯中磁感应强度的影响.随振子齿厚度的增大，振子与磁轭磁齿相对面积也逐渐增大，铁芯中磁感应强度呈不断变大的趋势，但随着振子齿的不断增大，振子运动过程中开始与前后左右磁轭均有接触的可能性会增大，漏磁也会增加.选择适当的振子齿厚度，可以有效减小图4(c)时铁芯中磁感应强度，改善边缘效应和减小整个装置运行过程中的漏磁.从图5(c)中可以看出：该装置在振子齿厚度大于2.1 mm之后磁感应强度开始逐渐减小，所以本装置的振子齿厚度选择2.1 mm.建模时，为保证图4(a)时振子齿与磁轭上的磁齿对应，振子两齿之间最小间距为4 mm.

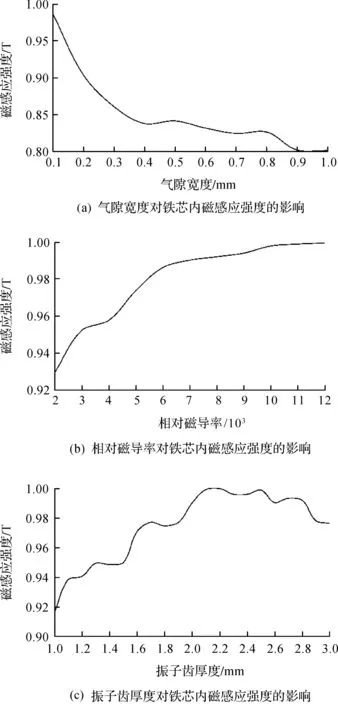
图5 静态仿真结果Fig.5 Static simulation results

3 仿真结果

根据结构尺寸，Maxwell动态仿真设置振子以2 m/s做匀速运动，振动频率为20 Hz.磁轭上的每个铁芯设置500 匝线圈.参数优化前的装置，位于图4(a)时的空气气隙定为0.2 mm，导磁材料相对磁导率为2 000，振子齿厚为1.5 mm.参数优化后的装置，空气气隙定为0.1 mm，导磁材料相对磁导率为6 000，振子齿厚为2.1 mm，其他参数保持不变.动态仿真结果如图6，7所示.优化前的结构，单个线圈产生的总感应电动势幅值约为0.4 V，4 个线圈总的电动势为1.6 V；优化后的单个线圈感应电动势幅值约为1.2 V，4 个线圈总电压值为4.8 V.优化后的装置能量收集效率为优化前的3 倍.图8是优化后振子运动过程中对磁轭内磁感应强度的影响结果图.

图6 未优化结构动态仿真结果Fig.6 The dynamic simulation results of the non-optimized structure

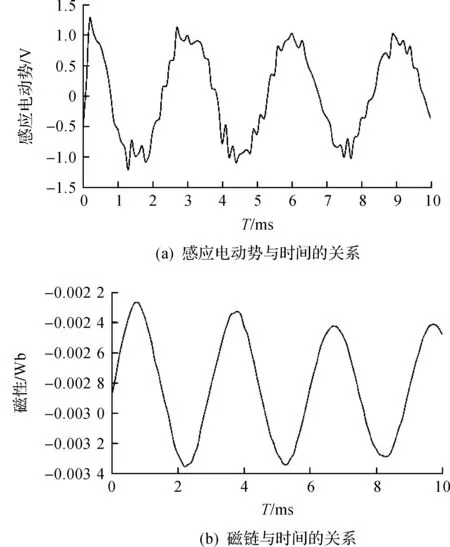
图7 优化后结构的动态仿真结果Fig.7 Dynamic simulation results of optimized structure

图8 振子位置变化对磁轭内磁感应强度的影响Fig.8 The influence of the change of the position of the vibrator on the magnetic induction in the yoke

4 结 论

新型方形振子电磁式振动能量收集装置结构简单，环境适应性强，可在人体的摆动、水面的波动和机械的震动等多种环境中工作.而且考虑到气隙对闭合磁路的影响，设计出了齿状磁轭，增加了磁通量交变次数，使能量收集装置可以在低频环境中工作，提高了装置的工作效率.通过分析结构主要参数变化对铁芯中最大磁感应强度的影响获得装置结构最优值，最大程度地提高能量的利用率.利用Ansoft Maxwell进行动态仿真，该装置在2 m/s振动速度下，产生的总的感应电动势可达4.8 V，最大带负载功率为118.5 mW.因此新型方形振子能量收集装置使用的多磁齿结构极大地提高了装置的能量收集效率，具有很大的发展前景.

[1] 龙胜春，龙军.一种应用与无线传感器网络的数据压缩方法[J].浙江工业大学学报，2014，42(2)：210-213.

[2] 周晓，李杰，边裕挺.基于无线传感网络的温度检测系统设计[J].浙江工业大学学报，2013，41(4)：440-443.

[3] 姚明海，陈占省，顾勤龙.基于REST架构的离散制造业物联网平台[J].浙江工业大学学报，2015，43(4)：425-430.

[4] 陈勇，丁杰雄.电磁型振动能量收集器研究及发展现状[J].微纳电子技术，2012，49(8)：534-541.

[5] 文玉梅，江小芳，李平，等.一种采用复合磁电换能器的振动能量采集器[J].仪表技术与传感器，2009(z1)：372-375.

[6] 何鹏举，巫世杰，夏亮，等.压电悬臂梁采收低频振动能的理论分析与仿真[J].仪表技术与传感器，2009(10)：91-96.

[7] 孟庆春，陈光柱.自供电无线传感网络节点设计[J].仪表技术与传感器，2012(7)：102-104.

[8] CHING N H, WONG H Y. A laser micro machined multi-model resonating power transducer for wireless sensing systems[J]. Sensors and actuators A: physical, 2002, 97: 685-690.

[9] TRICHES M, WANG F. A MEMS energy harvesting device for vibration with low acceleration[J]. Procedia engineering, 2012, 47: 770-773.

[10] MANN B P, SIMS N D. Energy harvesting from the nonlinear oscillations of magnetic levitation[J]. Journal of sound and vibration, 2009, 319: 515-530.

[11] 王佩红，刘慧婷，杨卓青,等.基于MEMS技术的三明治型电磁式微振动能量采集器[J].纳米技术与精密工程，2010，8(6)：510-515.

[12] ENRICO D, MARCO M, GIUSEPPE V. Analytical model of a vibrating electromagnetic harvester considering nonlinear effects[J]. IEEE transactions on power electronics, 2010, 25(8): 1989-1997.

[13] JAMES M, FAROQ B. Comparison of energy harvesting systems for wireless sensor networks[J]. International journal of automation and computing, 2008, 5(4): 334-347.

[14] BEEBY S P, TUDOR M J, TORAH R N. Experimental comparison of macro and micro scale electromagnetic vibration powered generators[J]. Micro-system technologies, 2007, 13: 1647-1653.

[15] ELHAMI M, GLYNNE J P, WHITE N M, et al. Design and fabrication of a new vibration-based electromechanical power generator[J]. Sensors and actuators A: physical, 2001, 92: 335-342.

[16] 邹继斌.磁路与磁场[M].哈尔滨：哈尔滨工业大学出版社，1998.

[17] KWON S D, PARK J K, LAW K. Electromagnetic energy harvester with repulsively stacked multi-layer magnets for low frequency vibrations[J]. Smart materials and structures, 2013, 22(5): 71-78.

[18] SAHA C, DONNEL T, WANG N, et al. Electromagnetic generator for harvesting energy from human motion[J]. Sensors and actuators A: physical, 2008, 147(4): 248-253.

[19] 杨燕花.微型直线式振动能电能转换模型的结构与性能研究[D].哈尔滨：哈尔滨理工大学，2011.