基于格型结构的IIR数字滤波器硬件实现

， ，

(1. 浙江工业大学 信息工程学院，浙江 杭州 310023；2. 杭州国芯科技股份有限公司 浙江 杭州 310012； 3. 浙江财经大学 信息学院，浙江 杭州 310018)

数字滤波器是数字信号处理系统中重要的组成部分[1-3]，一般分为有限冲激响应(Finite impulse response - FIR)滤波器和无限冲激响应(Infinite impulse response - IIR)滤波器两种.FIR滤波器在实际应用中有很多吸引人的特性，譬如线性相位、能保证绝对稳定、不会产生自激振荡等，但对于同样的设计要求，IIR滤波器比FIR滤波器需要的阶数低，更有利于节省硬件资源，因此近年来随着智能优化算法在数字滤波器设计领域的成功应用，对于IIR滤波器实现问题的研究越来越广泛.一个设计好的数字滤波器可以用许多种不同的结构来实现，它们在无限精度下都是等价的，但基于物理器件有限精度实现时，不同的实现结构有着不同的数值特性，因此在数字滤波器设计与实现过程中，结构的选择对整个数字系统的性能起着非常重要的作用.希望一个滤波器结构实现复杂度低，且参数的有限字长(Finite word length - FWL)效应敏感度比较低，即用比较少的位数就能满足性能和稳定性的要求，从而节省硬件资源.

目前关于IIR滤波器的硬件实现大多以二阶级联结构为基础[4-7]，该结构便于调整滤波器的频率响应性能，稳定性的判决也相对简单，但对FWL效应比较敏感，且硬件实现时多以直接量化为主，没有经过优化，需要的系数位数较长，不利于IIR滤波器的低成本实现.而格型结构是参数敏感度比较低的一种滤波器实现结构，目前在功率谱估计、语音处理、自适应滤波等领域应用广泛，文献[8]中提出了一种新型格型结构，该结构参数敏感度低，采用遗传算法可以高效地找到满足滤波器性能要求的离散参数[9-11]，且实现复杂度低，有利于促进IIR滤波器的实用化.应用这种结构，对参数离散化的IIR滤波器实例基于FPGA进行硬件实现，并利用Quartus II软件对实现结果进行综合和仿真.

1 新格型结构

图1为文献[8]中提出的一种注入式和抽头式相结合的新格型结构.

图1 一种注入式和抽头式相结合的格型结构Fig.1 A “ injected numerator ” and “ tapped numerator ” hybrid lattice structure

此格型结构对应的参数向量η为

η

(1)

式中：KK1…KN；θθ0…θN-1；ψψ0…ψN.

θ为注入系数，将输入信号u(n)通过参数θ0,…,θN-1加权后接入到各个格型单元，而格型结构的输出y(n)由b0(n)和N个格型单元的后向输出b1(n),…,bN(n)通过抽头系数ψ0,…,ψN加权得到.格型单元Km有多种结构，在实现时选择计算复杂度较低的单乘法器结构[5]，如图2所示.

图2 单乘法器结构Fig.2 One -multiplier lattice structure

滤波器传输函数H(z)可写为

(2)

式中：aa1…aN；bb0…bN.

众所周知：K和a具有一一对应的关系，而文献[8]中给出的b与参数η的关系为

b=Mbψ

(3)

式中Mb取决于K，θ.

实现图1中的N阶格型结构需要3N+1个乘法器，但其参数敏感度较低，文献[9-10]中采用智能优化中的遗传算法，对较低阶IIR滤波器采用全局参数离散化方法，对较高阶IIR滤波器采用分步参数离散化方法，得到了比直接量化更低的实现复杂度，有效节省了硬件资源.且对于格型结构，只要在K系数的离散设计时绝对值小于1，就可以保证滤波器稳定.下面给出一个5 阶低通IIR滤波器实例，其性能要求：1) 通带边界0.1；2) 阻带边界0.135；3) 通带波动≤1 dB；4) 阻带衰减≥40 dB.

表1给出了经过优化得到的满足滤波器性能要求的格型结构离散参数，图3是其对应的滤波器幅频响应曲线.

表1 格型结构离散参数Table 1 Discrete parameters for lattice structure

图3 基于表1离散参数的滤波器幅频响应曲线Fig.3 The magnitude response of the filter based on the parameters of Table 1

从表1的离散参数可以看出：在满足性能要求的情况下，参数θm的敏感度很低，与输入信号u(n)相乘时不需要加法器，参数ψm和Km参与乘法时需要的加法器个数也较少，因此有利于节省IIR滤波器硬件实现时的资源消耗.

2 基于格型结构的硬件实现

下面以上节中的5 阶低通IIR滤波器为例说明硬件实现方法.格型结构具有模块化结构，因此可以将图1中输入到输出的计算过程分成3 部分：

1) 参数θm与输入信号u(n)的乘法以及与格型单元前向信号fm(n)的加法.

2) 图2对应的参数Km单乘法器格型单元.

3) 参数ψm与格型单元后向信号bm(n)的乘法以及得到输出信号y(n)的加法.

采用Verilog HDL语言进行RTL级描述，在Quartus II软件下基于FPGA进行编译和综合.对应的程序结构如图4所示.

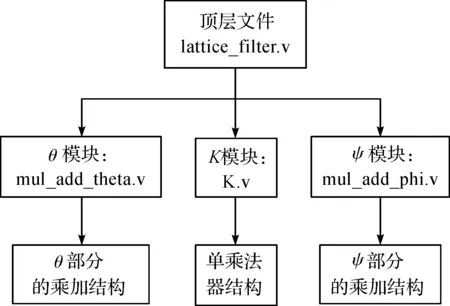
图4 Verilog HDL程序结构框图Fig.4 Verilog HDL program block diagram

在顶层文件lattice_filter中，首先定义3 组参数，为了硬件实现方便，进行了取整处理，θm放大4 倍，ψm和Km放大1 024 倍.由于参数有正有负，为方便补码运算，将参数的绝对值和符号分别给出，以Km参数为例：

parameter K1_abs = 888;

parameter K2_abs = 984;

……

parameter K5_abs = 496;

parameter K1_sign = 1; //符号位为1，表示负值

parameter K2_sign = 0;

……

parameter K5_sign = 1;

然后分别调用N次mul_add_theta.v模块，N次K.v模块和N+1次mul_add_phi.v模块，各模块程序如下：

(1) mul_add_theta.v模块的主要程序

assign temp_mult = add_0 ❋ theta_abs;

assign temp_sign = theta_sign ? (～temp_mult+26'd1) : temp_mult;

assign sum = temp_sign + add_1;

(2) K.v模块的主要程序

assign temp_sub = fm-bm_reg;

assign temp_mul = {{10{temp_sub[25]}},temp_sub} ❋ Km_abs;

//符号位扩展

assign temp_sign = Km_sign ? (～temp_mul+36'd1) : temp_mul;

//根据K系数的符号位进行补码操作

assign temp_div = temp_sign[35] ? (temp_sign + 26'd511) : (temp_sign + 26'd512); //四舍五入

assign fm_1 = temp_div[35:10] + fm;

assign bm = temp_div[35:10] + bm_reg;

(3) mul_add_phi.v模块的主要程序

assign temp_mult = add_0 ❋ theta_abs;

assign temp_sign = theta_sign ? (～temp_mult+26'd1) : temp_mult;

assign sum = temp_sign + add_1;

最后的输出要根据参数取整的放大倍数进行截短处理.

3 仿真与结果分析

仿真也在Quartus II软件下进行.为了分析滤波器是否达到预期的低通滤波功能，采用DDS技术通过Verilog HDL编程实现了一个正弦信号发生器模块，通过对不同频率正弦信号的滤波结果分析该格型结构滤波器的功能.系统联调的顶层模块如图5所示.

图5 系统联调的顶层模块图Fig.5 The top module diagram of system simulation

输入的系统时钟clock_in设置为32.768 MHz，sin_generator模块是正弦信号发生器，其查找表存入一个正弦信号完整周期的64 个等间隔采样数据，因此可以输出正弦信号频率的最大值为32.768 MHz/64=512 kHz，也可以方便输出多个正弦信号的叠加信号.freseprate模块是分频器，将系统时钟clock_in进行128 分频，输出的时钟信号：clk_out=32.768 MHz/128=256 kHz.将clk_out信号送入到格型滤波器lattice_filter模块，作为格型滤波器的采样时钟fs，即

fs=256 kHz

(4)

由滤波器性能指标及图3易知：1) 通带边界0.1×256 kHz =25.6 kHz；2) 阻带边界0.135×256 kHz =34.56 kHz.为了验证该滤波器的功能，选择位于通带边界附近的25 kHz正弦信号和位于阻带边界附近的35 kHz正弦信号的叠加作为格型滤波器的输入信号u_n，对应的仿真波形如图6所示，输出信号y_n中只保留了25 kHz的低频信号.

图6 25 kHz+35 kHz正弦信号的滤波效果Fig.6 Filtering effect of 25 kHz+35 kHz sine signal

对通带和阻带内的其他频率信号也进行了仿真，以验证该格型滤波器的滤波功能.以通带内10 kHz正弦信号和阻带内50 kHz正弦信号为例，图7，8分别给出了相应的滤波效果.

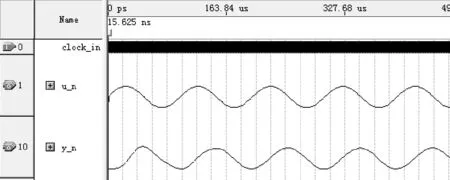
图7 10 kHz正弦信号的滤波效果Fig.7 Filtering effect of 10 kHz sine signal

图8 50 kHz正弦信号的滤波效果Fig.8 Filtering effect of 50 kHz sine signal

4 结 论

对于同样的设计要求，IIR滤波器比FIR滤波器需要的阶数低，更有利于节省硬件资源，但其设计与实现都更加复杂，而且还与滤波器的稳定性有关，因此人们一直在不断研究有效的IIR滤波器设计实现方法.基于一种新型格型结构，提出了一种IIR数字滤波器的硬件实现方法，并通过仿真验证了其滤波功能的正确性.由于该格型结构实现复杂度低，且抵抗FWL效应的能力强，因此可以有效促进IIR滤波器的实用化，对数字系统的高效低成本实现具有一定应用价值.

[1] 金燕,王明,葛远香.基于FPGA的抗混叠FIR数字滤波器的设计与实现[J].浙江工业大学学报,2010,38(2):192-196.

[2] 张玉华,彭宏,郑冕,等.基于GSM射频拉远系统的CIC滤波器的设计[J].浙江工业大学学报,2011,39(1):109-113.

[3] 邵奇可,解洋,张江,等.具有通信约束的网络化控制系统LQG控制器设计[J].浙江工业大学学报,2015,43(1):103-109.

[4] 屈星,唐宁,严舒,等.基于FPGA的IIR数字滤波器的设计与仿真[J].计算机仿真,2009,26(8):304-307.

[5] 姚若河,彭亮,石磊.IIR数字滤波器的FPGA实现[J].中国集成电路,2005(9):53-55.

[6] 曾菊容.高阶IIR滤波器的FPGA实现[J].电子设计工程,2011,19(10):173-175.

[7] 杨延亮,程知群,冯涛.基于FPGA的IIR带通数字滤波器设计与仿真[J].电子世界,2012(3):14-15.

[8] LI Gang, LIM Y C, HUANG Chaogeng. Very robust low complexity lattice filters[J]. Signal processing IEEE transactions on signal processing, 2010, 58(12):6093-6104.

[9] XU Hong, HUANG Chaogeng, YE Feng. Design of lattice-based digital IIR filters with discrete coef?cients[C]//International Conference on Natural Computation. Shenyang: IEEE, 2013: 734-738.

[10] XU Hong, HUANG Chaogeng, YE Feng, et al. A novel discrete coefficient IIR digital filter design based on a lattice structure[C]//International Conference on Industrial Electronics and Applications. Hangzhou: IEEE, 2014: 743-747.

[11] LI Gang, LIM Y C, HUANG Chaogeng, et al. A novel digital IIR filter design strategy-structure-based discrete coefficient filters[C]//International Symposium on Circuits and Systems. Seoul: IEEE, 2012:37-40.