形式三角矩阵环上的PC-内射模

夏国利， 王芳贵*, 蒲永燕

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066； 2. 攀枝花学院 数学与计算机学院, 四川 攀枝花 617000)

1 预备知识

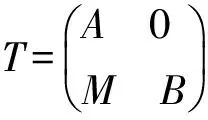
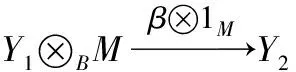
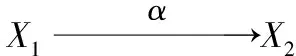
Goodearl在文献[7]中研究了形式三角矩阵环的Noether性,即T是右Noether环当且仅当A、B是右Noether环,且M是有限生成右A-模,此外,文献[7]还对T上的有限生成模进行了刻画,即右T-模(X,Y)f是有限生成模当且仅当Y是有限生成右T-模,cok(f)是有限生成右A-模.Haghany等[8-9]研究了形式三角矩阵环的极小内射性、投射性、投射生成子以及投射盖等性质,得出T-模(P,Q)g是投射模当且仅当Q是投射右B-模,g:Q⊗BM→P是单同态,且cok(g)是投射右A-模.Chen等[1]研究了Morita系统环上的自由模,进一步刻画了形式三角矩阵环上的自由模与投射模.设λ为任意非空集合,则T-模(X,Y)f≅T〈λ〉当且仅当X/f(Y⊗M)≅A〈λ〉,Y≅B〈λ〉.叶飞[10]分别给出了T-模是有限表现的充分条件和必要条件,即设(X,Y)f是T-模，若(X,Y)f有限表现,则cok(f)是有限表现右A-模,且Y是有限表现右B-模;反之,若cok(f)是有限表现右A-模,Y是有限表现右B-模,且ker(f)是有限生成右A-模,则(X,Y)f有限表现.Asadollahi等[11]研究了形式三角矩阵环上模的Ext函子的消失问题,并详细刻画了该环上投射和内射维数有限的模结构.Krylov等[12]又研究形式三角矩阵环上模的内射性、投射性、平坦性以及遗传性等性质.

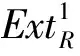
2 形式三角矩阵环的凝聚性

引理2.1设(P,Q)g是T-模，则有:

1) (P,Q)g是自由(投射)模当且仅当Q是自由(投射)右B-模,g:Q⊗BM→P是单同态,且cok(g)是自由(投射)右A-模;

2) (P,Q)g是有限生成自由(投射)模当且仅当Q是有限生成自由(投射)右B-模,g:Q⊗BM→P是单同态,且cok(g)是有限生成自由(投射)右A-模.

证明参见文献[8].

引理2.2右T-模(X,Y)f是有限生成模当且仅当Y是有限生成右T-模,cok(f)是有限生成右A-模.

证明参见文献[15].

命题2.3设M是有限生成A-模,则右T-模(X,Y)f是有限生成模当且仅当X是有限生成右A-模,Y是有限生成右B-模.

证明由正合列Y⊗BM→X→cok(f)→0即得.

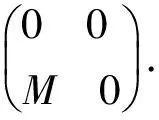
引理2.4对右T-模(X,Y)f,有

(X,Y)f/(X,Y)fΩ≅cok(f)×Y.

证明设x∈X,y∈Y,m∈M,有

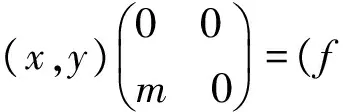
因此有(X,Y)fΩ=(f(Y⊗SM),0),故有(X,Y)f/(X,Y)fΩ≅(X,Y)/(f(Y⊗M),0)≅cok(f)×Y.

命题2.5若(X,Y)f是有限表现右T-模,则cok(f)是有限表现右A-模,且Y是有限表现右B-模.

证明由引理2.4即得.

定理2.6设A是右凝聚环,则右T-模(X,Y)f是有限表现模,当且仅当Y是有限表现右B-模,cok(f)是有限表现右A-模,且ker(f)是有限生成右A-模.

证明设(X,Y)f是有限表现右T-模.由命题2.5,cok(f)是有限表现右A-模,Y有限表现右B-模.设

(1)

是正合列,其中(P,Q)g有限生成投射右T-模,(K,L)是(P,Q)g的有限生成子模.于是下面的2行是正合列的交换图:

由蛇形引理,有正合列

(2)

由引理2.2,cok(g)是有限生成投射A-模,且cok(h)是有限生成A-模.由cok(f)是有限表现的,以及A是右凝聚环,故ker(cok(g)→cok(f))是有限表现模,因此还有ker(f)是有限生成的.

假设反之条件成立.由引理2.2知(X,Y)f是有限生成右T-模.现在仍考察正合列(1),只假设(P,Q)g是有限生成投射右T-模,故有正合列

和正合列

由于Y是有限表现B-模,故L是有限生成B-模.仍考虑正合列(2).由于cok(f)是有限表现的,故ker(cok(g))→cok(f))是有限生成的.由于ker(f)是有限生成的,故cok(h)是有限生成的.从而有(K,L)h是有限生成T-模,因此(X,Y)f是有限表现T-模.

定理2.7设A是右凝聚环,M是有限表现右A-模,则右T-模(X,Y)f是有限表现模当且仅当X是有限表现右A-模,Y是有限表现右B-模.

证明首先,当(P,Q)g是有限生成投射模时,则由引理2.1,有g是单同态.由正合列

以及Q⊗BM是有限表现右A-模,知P是有限表现右A-模.

若(X,Y)f是有限表现右T-模,则由定理2.6知Y是有限表现右B-模.

仍考虑正合列(1),其中(P,Q)g是有限生成投射右T-模,(K,L)h是有限生成右T-模.由

是正合列,且由L⊗BM与cok(h)都是有限生成A-模,有K是有限生成的.由正合列0→K→P→X→0知X是有限表现A-模.

反之,设X是有限表现A-模,Y是有限表现B-模.于是K是有限生成A-模,cok(h)是有限生成模.从而cok(f)是有限表现A-模.考虑正合列(2),由于A是右凝聚环,ker(cok(g)→cok(f))是有限表现A-模,从而ker(f)是有限生成的.由定理2.6,(X,Y)f是有限表现右T-模.

设R是环.回顾右R-模X称为伪凝聚模,是指X的任何有限生成子模是有限表现模.显然,伪凝聚模X是凝聚模当且仅当X是有限生成的.

定理2.8设A是右凝聚环,M是有限表现右A-模,则右T-模(X,Y)f是伪凝聚右T-模当且仅当X是伪凝聚右A-模,Y是伪凝聚右B-模.

证明设(X,Y)f是伪凝聚右T-模.设X0是X的有限生成A-子模,则(X0,0)是(X,Y)f的有限生成T-子模.于是(X0,0)是有限表现T-模,从而X0是有限表现A-模,故X是右凝聚A-模.

设Y0是Y的有限生成B-子模,则(Y0⊗BM,0)f是(X,Y)f的有限生成子模.令X0=f(Y0⊗BM),则X0是X的有限生成A-子模.由命题2.3,(X0,Y0)f是有限生成的T-模.故(X0,Y0)f是有限表现T-模,从而Y0是有限表现的B-模.故Y是伪凝聚B-模.

假设反之条件成立.设(X0,Y0)f是(X,Y)f的有限生成T-子模.仍由命题2.3,X0是有限生成A-模,Y0是有限生成B-模.故X0是有限表现A-模,Y0是有限表现B-模.由定理2.6,(X0,Y0)f是有限表现T-模,故(X,Y)f是伪凝聚T-模.

推论2.9设M是有限表现右A-模,则T是右凝聚环当且仅当A与B都是是右凝聚环.

3 形式三角矩阵环上的PC-内射模

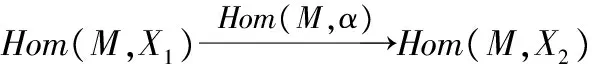
引理3.1对任给的T-模(X,Y)f,有如下同构:

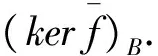
(3)

证明参见文献[11].

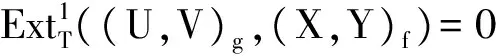
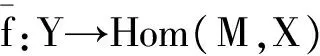
证明参见文献[11].

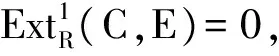
引理3.3设R是右凝聚环,E是PC-内射模,则idRE≤1.

证明参见文献[14]中的定理7.

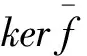
证明设(X,Y)f是PC-内射模.由引理3.3,idT(X,Y)f≤1.对任给的伪凝聚右A-模U,由定理2.8知(U,0)是伪凝聚T-模,因此

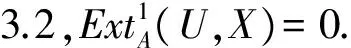
对任何伪凝聚右B-模V,仍由定理2.8,(0,V)是伪凝聚B-模.同理得到

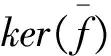
是正合列.因(M,B)δ是有限表现T-模,从而也是伪凝聚T-模,故有正合列

(4)

考虑自然同态

Φ:HomT((M,B)δ,(X,Y)f)→HomB(B,Y),
Φ(α,β)=f(β⊗1M),

其中

(α,β)∈Hom((M,B)δ,(X,Y)f).

对任何

(α,β)∈Hom((M,0),(X,Y)f),

显然有β=0.令Ψ(α,0)=αδ-1,则容易验证

Ψ:HomT((M,0),(X,Y)f)→HomB(M,X)

是同构,且有下面的交换图:

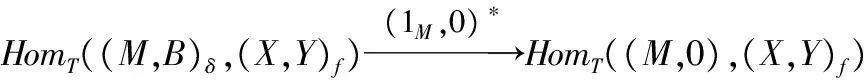
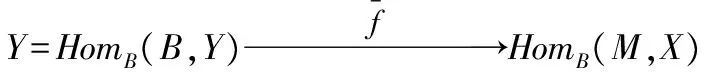
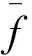
现在假设反之的条件成立.设

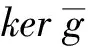
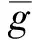
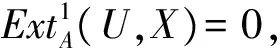
推论3.5设T是右凝聚环,M是有限表现右A-模,则有:

1) (X,HomA(M,X))1HomA(M,X)是PC-内射右T-模当且仅当X是PC-内射右A-模;

2) (0,Y)是PC-内射右T-模当且仅当Y是PC-内射右B-模.

定理3.6设T是右凝聚环,M是有限表现右A-模,X是PC-内射右A-模,则idT(X,0)≤1.

证明记f=1HomA(M,X).由推论3.5,

(X,HomA(M,X))1

是PC-内射右T-模.设

0→(X,HomA(M,X))f→(E1,E2)g→(C1,C2)h→0

是T-模正合列,其中(E1,E2)g是内射T-模.用Hom(T/J,-)作用于上正合列可得

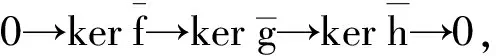
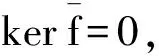
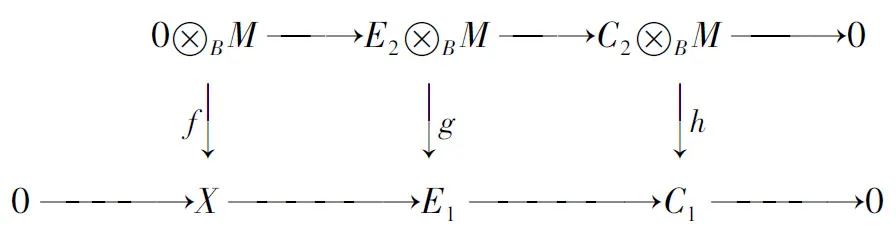
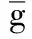
致谢四川师范大学研究生优秀论文培育基金(校研字20160902)对本文给予了资助,谨致谢意.

[1] CHEN J L, ZHANG X X. On modules over formal triangular matrix rings[J]. East-West J Math,2001,3(1):69-77.

[2] HAGHANY A. Injectivity conditions over a formal triangular matrix ring[J]. Arch Math,2002,78(4):268-274.

[3] LI Q S, TONG W T. On the structure of triangular matrix rings[J]. Northeast Math J,2003,19(1):51-56.

[4] CHEN X W. Singularity categories, schur functors and triangular matrix rings[J]. Algeb Represent Theory,2009,12(2):181-191.

[5] CHEN H Y. On the structure of triangular matrix rings[J]. J Nanjing Univ Math Biquarterly,1999,16(2):153-157.

[6] AUSLANDER M, REITEN I, SMALO S O. Representation Theory and Artin Algebras, Cambridge Studies in Advanced Math[M]. Cambridge:Cambridge University Press,1995.

[7] GOODEARL K R. Ring Thoery, Nonsingular Rings and Modules[M]. New York:Marcel Dekker Inc,1976.

[8] HAGHANY A, VARADARAJAN K. Study of formal triangular matrix rings[J]. Commun Algebra,1999,27(1):5507-5525.

[9] HAGHANY A, VARADARAJAN K. Study of modules over formal triangular matrix rings[J]. J Pure Appl Algebra,2000,147(1):41-58.

[10] 叶飞. 形式三角矩阵环上的有限表现模[J]. 大学数学,2006,22(1):80-82.

[11] ASADOLLAHI J, SALARIAN S. On the vanishing of Ext over formal triangular matrix rings[J]. Forum Math,2006,18(6):951-966.

[12] KRYLOV P A, TUGANBAEV A A. Modules over formal matrix rings[J]. Math Sci,2010,171(2):248-295.

[13] BOURBAKI N. Algebre Commutative[M]. Paris:Hermann,1961.

[14] 夏国利,王芳贵. PC-内射模及其刻画[J]. 黑龙江大学学报(自然科学版),2016,33(4):466-471.

[15] GOODEARL K R, WARFELD R B. An introduction to non-commutative noetherian rings[C]//London Math Soc, Student Texts,16. London:Cambridge University Press,1989.