代数和模的控制维数
2018-03-23惠昌常
惠昌常
(1. 首都师范大学 数学科学学院, 北京 100048; 2. 河南师范大学 数学与信息科学学院, 河南 新乡 453007)
1 控制维数的定义和著名的Nakayama猜想
在环与代数的研究中,利用同调性质或维数来分类代数和模是一个常用而且非常有效的方法.控制维数的引入就是一个典型的例子.早在1958年,Nakayama[1]就提出利用代数的控制维数来分类代数.我们回顾一下控制维数定义的历史和最终的定义.
总假设A是域k上的一个有限维代数,并限定在代数A的有限生成左模范畴A-mod中讨论问题.将代数A的有限生成的右模范畴记作mod-A,或Aop-mod,其中Aop表示A的反代数;代数A的有限生成A-A-双模范畴记作A-mod-A,或Ae-mod, 这里Ae表示代数A的包络代数A⊗kAop.在双模范畴Ae-mod中考察代数A的一个双模正合序列
0→AAA→I0→I1→…→In-1,
其中I0,I1,…,In-1作为双模,既是投射的也是内射的.Nakayama在文献[1]中提出按照这种分解的长度来分类代数,并猜想:如果一个代数存在一个无限长的这种内射分解,则这个代数必定是自入射的,即AA是一个内射模.随后,Tachikawa[2]研究了具有这种分解的代数,证明了在长度n>0的情况下它们都是QF-3代数,即具有极小忠实投射-内射模的代数.Tachikawa在文献[3]中放松了上述的分解条件,即只在A-mod中来讨论上述问题,也给出了相应的猜想.这样,一个代数A的控制维数记作
dom.dim(A),
就定义为:在AA的极小内射分解
0→AA→I0→I2→…→In→…
中使得I0,I1,…,In-1为投射模的最大的自然数n.严格地讲,这样定义的控制维数应该叫做“左控制维数”.当然这里一个很自然的问题是:如果用右模来定义,得到的右控制维数又会是怎样的呢?左、右控制维数相等吗?在文献[4]中,Müller证明了对于一个有限维代数A来说,它的左控制维数、右控制维数和Nakayama定义的双边控制维数都是相等的.这就是为什么今天在讨论代数的控制维数时,只用左模来定义控制维数就够了.显然,自入射代数的控制维数是无限的.这句话的逆命题就是Nakayama猜想了,它可以叙述为:
Nakayama猜想设A是域上的一个有限维代数,如果dom.dim(A)=∞,则A是自入射代数,即AA是内射模.
这个猜想也列在著名代数表示理论专家Auslander等在1995年出版的专著中(文献[5]的猜想(8)),已有60年的历史了,但它依然是公开问题.对于分次的代数,这个猜想是成立的[6-7].
为了叙述方便,将控制维数的定义扩展到任意的A-模X上.设
0→AX→I0(X)→I1(X)→…→In(X)→…
是X的一个极小内射分解.设I是一个内射A-模,0≤n ≤∞.如果n是使得所有I0,I1,…,In-1都属于add(I)的最大者,就说X关于I的控制维数是n,记作
I-dom.dim(X)=n,
这里add(I)表示在A-mod中由I生成的可加满子范畴.当add(I)是所有投射-内射模构成的范畴时,把
I-dom.dim(X)
简单写作dom.dim(X),并称它为X的控制维数.
2 控制维数对代数的分类
在20世纪60年代的后期,Müller在控制维数方面做了大量有意义的工作[8-9],包括前面提到的一些工作.这里介绍利用控制维数对代数分类的一些结果.先回忆一些概念.
设A是一个k-代数,M是一个A-模.称M为极小忠实模,如果它是忠实的(faithful),并且对任意的忠实模N都有一个直和分解:N≃M⊕N′,其中N′是一个A-模.代数A叫做QF-3代数,如果它有一个极小忠实左模和极小忠实右模.注意,极小忠实模一定是投射的.模AM叫做生成子,如果每个不可分解投射模都同构于M的一个直和项;叫做余生成子,如果每个不可分解内射模都同构于M的一个直和项;叫做生成-余生成子,如果它既是生成子也是余生成子.在一些文献上,生成-余生成子也叫做完全忠实模(fullyfaithfulmodule).
定理2.1假设A是一个有限维k-代数.
1)dom.dim(A)≥1当且仅当A是QF-3代数[2].
2)dom.dim(A)≥2当且仅当存在一个代数B,一个生成-余生成子BV,使得A≃EndB(V)[4].
事实上,Müller[4]证明了如下更一般的事实.
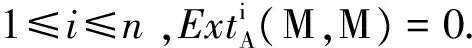
Hoshino[10]给出控制维数至少是2的代数的另一种刻画.
命题2.3[10]设R是左、右Noether环,则dom.dim(R)≥2当且仅当函子()**:R-mod→R-mod是左正合的,这里()*:=HomR(-,R).
Hoshino的上述结论被Colby在文献[11]中利用倾斜模(定义见本文第4节)的控制维数做了大幅度的推广.
对于任意的n,目前还没有见到对控制维数是n的这类代数的刻划.如果将控制维数和整体维数相结合来刻划代数,这方面的工作首先是Auslander对整体维数不超过2,控制维数至少是2的代数进行的刻划,他证明了这类代数是表示有限型代数的可加生成子的自同态代数[12],这类代数称为Auslander代数.近年来,Iyama等[13]讨论了整体维数不超过n,控制维数至少是n的代数.
控制维数在张量积下有如下的计算公式[4]:对任意的k-代数R和S,
dom.dim(R⊗kS)=
min{dom.dim(R),dom.dim(S)}.
对于控制维数无限的代数,Martinez-Villa利用函子反变有限子范畴(contravariantlyfinitesubcategory)研究了相关的挠对(torsionpair)和代数的自入射性,更详细的讨论见文献[14-15].
最后指出,在Frobenius扩张下,控制维数与几乎凝聚环(almostcoherentring)的关系在文献[16]中有深入的研究.
3 控制维数与Schur代数
控制维数在Schur代数或更一般的q-Schur代数的上同调群研究中也扮演着一个特别有用的角色.假设k是一个域,n≥r是两个自然数,用S(k,n,r)表示域k上关于对称群Σr的Schur代数(详细定义见文献[17]).在Schur代数的模范畴和对称群代数的模范畴之间有一个Schur函子
F: S(k,n,r)-mod→kΣr-mod,
这个函子把S(k,n,r)-mod中具有Weyl模滤链的模范畴F映射到kΣr-mod中具有对偶Specht模滤链的模范畴F ′.文献[18]证明了这类模的上同调群之间有一个同构的关系,他们的结果是针对更广泛的一类代数而证明的,限制到Schur代数就有如下结论.
定理3.1[18]设域k是无限域,特征是p>0,n≥r≥p, 对任意的M∈F,任意的X∈S(k,n,r)-mod, 都有:

2)dom.dim(Sk(n,r))=2(p-1).
这个结果也推广了文献[19-20]中的相应结论, 事实上,在文献[19-20]中,要求p>5和n≥r.
关于控制维数与Schur-Weyl对偶的联系和一些应用,参见文献[21].
4 导出等价下控制维数的变化
在代数与范畴的研究中,有3种基本的等价关系是比较重要的,它们是Morita等价、稳定等价和导出等价.
我们知道如果两个代数的模范畴是等价的,就称这两个代数是Morita等价.这个概念最早源于Morita的著名工作[22].但就是这个今天经常要用到的工作,在一开始时并没有受到重视,所以这篇文章就只好发表在大学学报一级的杂志上了.由Morita等价的定义可以看出,控制维数在Morita等价下是不变的.
两个代数叫做稳定等价的,如果它们的稳定范畴是等价的.这里稳定范畴是指模范畴模掉投射模子范畴而得到的商范畴[5].容易看出,稳定等价不保持控制维数:域k上的2×2上三角代数与代数k[x]/(x2)是稳定等价的,但前者的控制维数是1,而后者的控制维数是无限.然而一种特殊的稳定等价-Morita型稳定等价保持控制维数.域k上的两个代数A和B叫做Morita型稳定等价,如果存在双模AMB和BNA使得M和N作为单边模都是投射的,且有双模同构:M⊗BM≃A⊕P,N⊗AM≃B⊕Q,其中P和Q分别是投射双A-模和投射双B-模[23].关于Morita型稳定等价有丰富的文献资料,如文献[24-30].
下面回顾导出等价的定义,为此先引入一些符号.
设R是一个有单位元的环,R-模构成的复形是指一个如下的序列
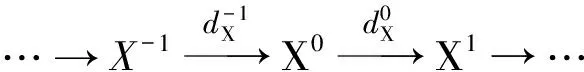
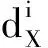
称dX为X•的微分.复形X•到Y•的态射是一簇的模同态(fi)i∈Z,其中fi:Xi→Yi满足
即对任意的i∈Z,有如下的交换图:
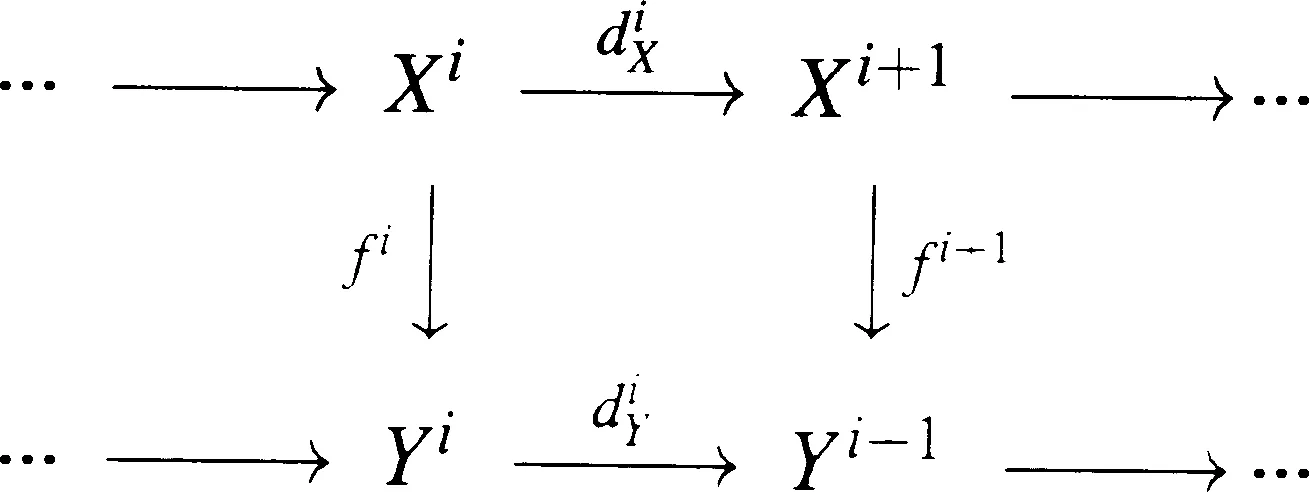
复形的态射可按照自然的方法合成.如果令C(R)表示R-模的所有复形的全体,则C(R)就构成一个范畴,容易看出,它是一个Abel范畴.利用这个复形范畴,可以定义它上面的同伦范畴(homotopycategory),记作K(R).如果一个复形

只有有限多个Xi不为0,就称它是一个有界复形.用Cb(R-proj)表示有限生成投射R-模的有界复形范畴,用Kb(R-proj)表示Cb(R-proj)的同伦范畴.


值得注意的是,D(R)的态射集合的描述比较复杂,有兴趣的读者可以参考文献[31].
导出范畴和等价或者更一般的三角范畴和等价(triangulatedcategoryandtriangleequivalence)是由大数学家Grothendieck和他的学生Verdier在20世纪的60年代引入的[32].1986年,Happel将三角范畴的理论和方法应用于有限维代数的表示理论的研究,取得了丰硕的成果[33-34].随后,Cline等[35]推广了Happel的结论到一般的环上,而Rickard[36]将Happel的这一想法做了全面的推广, 建立了环的导出范畴的Morita理论.
关于导出等价,Keller[37]从微分分次代数的角度作了深入的探讨,建立了微分分次代数的导出等价理论.限于篇幅,不在此进行介绍,建议读者阅读Keller的有关论文.下面叙述Rickard关于环的导出等价的一个主要结论.
两个环R和S称为是导出等价的,如果它们的导出范畴D(R)和D(S)作为三角范畴是等价的.例如,如果AT是一个倾斜A-模,Happel[33]证明了A与EndA(T)导出等价.关于环的导出等价有下面非常有用的结论.
定理4.1[36]环R和S是导出等价的充分必要条件是存在一个复形T•∈Kb(R-proj)使得:
1)HomK b (R-proj)(T•,T•[n])=0,对任意n≠0;
2)Kb(R-proj)可由T•作为可加、三角满子范畴生成;
3)S≃EndKb (R-proj)(T•).
如果Kb(R-proj)中的一个复形T•称满足条件1)和2),就称T•为R的一个倾斜复形(tiltingcomplexoverR).
容易看出,Morita等价的两个代数一定是导出等价的.反过来是不对的,这一点可由倾斜模(tiltingmodule)提供的导出等价看出来.现在的问题是:
问题1导出等价是不是保持控制维数?
对于几乎Nakayama-稳定的导出等价(almostν-stablederivedequivalence),控制维数是保持的[38].但一般来说,这个问题的答案是否定的,简单的例子就是:路代数k(•→•→•)与路代数k(•→•←•)是导出等价的,但前者的控制维数是1,而后者是0,因为这个代数就没有投射-内射模.于是,进一步的问题就是:
问题2如果2个代数是导出等价的,它们的控制维数之间会有什么样的变化规律?
问题3在什么条件下导出等价保持控制维数的有限性(或无限性)?
上述的2个问题,可以在下面2种特殊情况下进行讨论:
(a)在任意的代数类中讨论特殊的导出等价下控制维数的变化规律和无限性;
(b)在特定的代数类中讨论任意的导出等价下控制维数的变化规律和无限性.
关于这2种特殊情况,最新的结果是文献[39-40],其中文献[39]讨论情况(a),而文献[40]针对的是情况(b).现在对其中的一些结果进行介绍.
文献[39]首先给出构造导出等价的两个代数的方法,使得其中一个的控制维数至少是2,而另一个的控制维数是1.其次,讨论了倾斜模给出的导出等价下控制维数的变化规律.我们知道一个A-模T∈A-mod称为是倾斜模(tiltingmodule)[41],如果它满足:
1)T的投射维数有限,即pd(AT)=n<∞;
3) 存在一个正合列
0→AA→T0→…→Tn→0,Tj∈add(T),
这里add(T)表示在A-mod中由T生成的可加子范畴.
倾斜模的一个例子:设A的控制维数为n≥1,E(A)为AA的内射包,则U:=E(A)⊕(E(A)/A)就是一个投射维数小于等于1的倾斜模,且
dom.dim(AU)≥n-1,
见文献[11]中的命题5.如果dom.dim(A)=n,即有AA的一个极小内射分解
使得I0,I1,…,In-1是投射模,则也可以类似地定义一系列的倾斜模
Tj:=I0⊕…⊕Ij-1⊕Coker(dj-1),j=1,2,…,n,
这些模就称为典范倾斜模(canonicaltiltingmodules).

设T是一个倾斜模,将T先分解成两部分:T=P⊕T′,其中P是投射的,T′没有非零的投射直和项.进一步,将P再细分解:令E表示P的一个直和项,它满足
add(E)={X∈add(P)|νA(X)∈add(T)},
同文献[39]一样,称E是倾斜模T的心座(heart).令B:=EndA(T).关于A和B的控制维数,有下面的结论.
定理4.2[39]1) 如果ω∈add(νA(E)),则dom.dim(A) ≤dom.dim(B) +n;
2) 如果νA(E)∈add(ω),则dom.dim(B) ≤dom.dim(A) +n.
根据这个定理,如果
add(ω)=add(νA(E)),
则dom.dim(A)=∞当且仅当dom.dim(B)=∞.
这个定理将A和B的控制维数在假定的条件下联系起来了,那么是否有满足这些条件的代数和倾斜模呢?下面给出一类这样的代数.根据文献[42],一个k-代数A叫做Morita代数如果它同构于EndB(BB⊕M),其中B是自入射代数,M是一个B-模.
命题4.3设A是一个Morita代数,E0是AA的内射包,令
T:=E0⊕Ω-j(AA),
这里Ω-j(M)表示M的第j个余合冲(cosyzygy), 则:
1)倾斜模T:=E0⊕Ω-j(A)满足add(E)=add(ω),对任意1≤j 2)B:=EndA(E0⊕Ω-j(A))是Morita代数,对任意1≤j 3)dom.dim(B)=dom.dim(A),对任意 1 ≤j 关于Morita代数有以下命题. 命题4.4[39]设A是Morita代数,T是投射维数不超过n的倾斜模,令B:=EndA(T),则 dom.dim(A) ≤dom.dim(B)+n. 进而,如果B也是Morita代数,则 |dom.dim(A)-dom.dim(B)|≤n. 一般说来,Morita代数上的倾斜模的自同态代数不一定是Morita代数. 为了给出自同态代数的控制维数的下界,下面引入梯度的概念[39].根据倾斜模的知识,对给定的倾斜模T以及任意的投射模X,存在正合列 它是νA(X)的极小右add(T)-逼近,记 定义4.5[39]设T是一个倾斜A-模,E是T的心座,0→Pn→…→P0→T→T→0是T的一个极小投射分解,X是一个投射A-模. 1)X的T-梯度,记作∂T(X),定义为 2)代数A的T-梯度定义为∂T(AA),代数A的整体T-梯度定义为 ∂(A,T) :=min{∂T(Pi) +i|0≤i≤n}. 利用T-梯度,可以给出T的自同态代数的控制维数的一个下界,见文献[39]中的推论 4.12. 命题4.61)dom.dim(B) ≥∂(A,T)≥∂T(A); 2)∂T(A)=dom.dim(TB)=νA(E)-dom.dim(AT). 下面介绍在Morita代数类上导出等价对控制维数的影响规律. 定理4.7[40]假设A和B都是Morita代数, F: Db(A)→Db(B) 是一个三角等价,它对应的倾斜复形的非零项个数是n,则 |dom.dim(A)-dom.dim(B)| ≤n-1. 事实上,文献[40]讨论的特殊代数类要比Morita代数类广泛一些.命题4.4的第二个结论是定理4.7的一个特殊情况. 有例子表明,倾斜模自同态代数的控制维数不能用倾斜模的投射维数来界定.究竟它们应该是怎样的关系,依然是一个有待进一步考虑的问题. 1)Nakayama猜想的一些进展:对广义单列代数(generalizeduniserialalgebra)的生成-余生成子的自同态代数,Tachikawa[3]证明了Nakayama猜想成立. 2) 有限维数猜想,见文献[43]中的猜想(11):给了一个有限维代数A,定义A的有限维数为 fin.dim(A)=sup{pd(M)| M∈A-mod,pdA(M)<∞}. 有限维数猜想指fin.dim(A)<∞,这个猜想也是至今悬而未解.它与Nakayama猜想的关系是:如果fin.dim(A)<∞,则Nakayama猜想对A成立.因为如果 是A的一个极小内射分解,且所有Ij都是投射模,那么每个di的余核(Cokernel)如果不是投射模,那它就是一个投射维数为i+1的模.由于fin.dim(A)<∞,所以必有一个n使得dn的余核是投射模.这样,整个正合列 0→AA→I0→I1→…→Coker(dn)→0 就可裂,从而A是自入射代数. 所以,对有限维数有限的代数,Nakayama猜想成立.关于有限维数猜想的一些进展见文献[44]. 3)Tachikawa在文献[45]的第八章中还提出了与Nakayama猜想相关的一些猜想: (a) 域k上的代数A如果满足 对所有的i≥1都成立,则A必是自入射代数; 猜想(b)成立的情况在文献[45]中对p-群代数做了验证.这个猜想与下面的广义Nakayama猜想有关系. 4) 广义Nakayama猜想(generalizedNakayamaconjecture)是Auslander[46]在1975年研究Nakayama猜想时提出的一个猜想.如果 0→AA→I0→I1→… 关于这些猜想之间的蕴含关系,Yamagata在文献[48]中有详细的叙述.例如,任何一个猜想对代数A成立都意味着Nakayama猜想对代数A也成立,建议读者参看Yamagata的原文.这些猜想都没有完全解决,依然是公开问题.对特殊情况,已有一些验证.限于篇幅和本文的主题,在这里对它们不做介绍. 1) 设两个有限维代数A和B是导出等价的.如果A是Morita代数且dom.dim(B)≥2,那么B也是Morita代数吗? 2) 若两个有限维代数A和B是导出等价的,是否有A的控制维数是无限的,当且仅当B的控制维数是无限的? 3) 在什么条件下,导出等价的两个代数A和B有相同的控制维数? 4) 对导出等价下的一个代数等价类,是否存在控制维数的一个上界函数?如果有,是否有一个估算公式? 致谢本文的最后一稿是在2017年7—8月参加南方科技大学代数专题暑期学校期间完成的,对北京大学的张继平教授、南方科技大学的李才恒教授在暑期学校期间给予的帮助和支持,在此表示衷心地感谢.在此也感谢北京师范大学的刘玉明老师阅读初稿,并提出一些修改意见. [1]NAKAYAMAT.Onalgebraswithcompletehomology[J].AbhMathSemUnivHamburg,1958,22(1):300-307. [2]TACHIKAWAH.AcharacterizationofQF-3algebras[J].ProcAmMathSoc,1962,13(5):701-703. [3]TACHIKAWAH.OndominantdimensionofQF-3algebras[J].TransAmMathSoc,1964,112(2):249-266. [4]MÜLLERBJ.Theclassificationofalgebrasbydominantdimension[J].CanJMath,1968,20(9):398-409. [5]AUSLANDERM,REITENI,SMALØSO.RepresentationTheoryofArtinAlgebras[M].Cambridge:CambridgeStudiesinAdvancedMathematics,1995. [6]WILSONGV.TheCartanmaponcategoriesofgradedmodules[J].JAlgebra,1983,85(2):390-398. [7]FULLERKR,ZIMMERMANN-HUISGENB.OnthegeneralizedNakayamaconjectureandtheCartandeterminantproblem[J].TransAmMathSoc,1986,294(2):679-691. [8]MÜLLERBJ.Onalgebrasofdominantdimensionone[J].NagoyaMathJ,1968,31(31):173-183. [9]MÜLLERBJ.Dominantdimensionofsemi-primaryrings[J].JReineAngewMath,1968,1968(232):173-179. [10]HOSHINOM.Ondominantdimensionofnoetherianrings[J].OsakaJMath,1989,26(2):275-280. [11]COLBYRR.Tiltingmodules,dominantdimensionandexactnessofdualityfunctors[J].TsukubaJMath,1988,12:441-449. [12]AUSLANDERM.RepresentationDimensionofArtinAlgebras[M].Providence:AmMathSoc,1999:505-574. [13]IYAMAO,OPPERMANNS. n-representation-finitealgebrasandn-APRtilting[J].TransAmMathSoc,2011,363(12):6575-6614. [14]MARTINEZ-VILLAR.Algebrasofinifinitedominantdimension[J].TsukubaJMath,1994,18(1):9-20. [15]MARTINEZ-VILLAR.Inifinitedominantdimensionandtorsiontheories[J].CommunAlgebra,1994,22(11):4519-4535. [16]GMEZ-TORRECILLASJ,TORRECILLASB.FTFringsandfrobeniusextensions[J].JAlgebra,2002,248(1):1-14. [17]GREENJA.PolynomialRepresentationsofGLn[M]. 2nded.Berlin:Springer-Verlag,2007:161. [18]FANGM,KOENIGS.Schurfunctorsanddominantdimension[J].TransAmerMathSoc,2011,363(3):1555-1576. [19]HEMMERDJ,NAKANODK.SpechtfiltrationforHeckealgebrasoftypeA[J].JLondonMathSoc,2004,69(3):623-638. [20]KLESHCHEVAS,NAKANODK.Oncomparingthecohomologyofgenerallinearandsymmetricgroups[J].PacificJMath,2001,201(2):339-355. [21]KOENIGS,SLUNGARDIH,XICC.Doublecentralizerproperties,dominantdimension,andtiltingmodulese[J].JAlgebra,2001,240(1):393-412. [22]MORITAK.Dualityofmodulesanditsapplicationstothetheoryofringswithminimumcondition[J].SciRepTokyoKyoikuDaigaku,1958,A6:85-142. [23]BROUÉM.EquivalencesofBlocksofGroupAlgebras[M]//DlabV,ScottLL.FiniteDimensionalAlgebrasandRelatedTopics.Netherlands:Springer-Verlag,1994,424:1-26. [24]RICKARDJ.Derivedcategoriesandstableequivalence[J].JPureApplAlgebra,1989,61(3):303-317. [25]LINCKELMANNM.StableequivalencesofMoritatypeforself-injectivealgebrasandp-groups[J].MathZ,1996,223(1):87-100. [26]LIUYM,XICC.ConstructionsofstableequivalencesofMoritatypeforfinitedimensionalalgebrasIII[J].JLondonMathSoc,2007,76(1):567-585. [27]XICC.Stableequivalencesofadjointtype[J].ForumMath,2008,20(1):81-97. [28]DUGASA,MARTINEZ-VILLAR.AnoteonstableequivalencesofMoritatype[J].JPureApplAlgebra,2007,208(2):421-433. [29]HUW,XICC.DerivedequivalencesandstableequivalencesofMoritatypeI[J].NagoyaMathJ,2010,200(200):107-152. [30]LIUYM,ZHOUGD,ZIMMERMANNA.TwoquestionsonstableequivalencesofMoritatype[OL].arXiv:1409.1821,2014. [31]GELFANDSI,MANINYI.MethodsofHomologicalAlgebra[M].Berlin:Springer-Verlag,1996:372. [32]VERDIERJL.CatégoriesDérivées,EtatO[M].Berlin:Springer-Verlag,1977:262-311. [33]HAPPELD.Onthederivedcategoryofafinite-dimensionalalgebra[J].CommentMathHelv,1987,62(3):339-389. [34]HAPPELD.TriangulatedCategoriesintheRepresentationTheoryofFiniteDimensionalAlgebras[M].Cambridge:CambridgeUniversityPress,1988. [35]CLINEE,PARSHALLB,SCOTTL.DerivedcategoriesandMoritatheory[J].JAlgebra,1986,104(2):397-409. [36]RICKARDJ.Moritatheoryforderivedcategories[J].JLondonMathSoc,1989,s2-39(3):436-456. [37]KELLERB.Ondifferentialgradedcategories[C]//InternationalCongressofMathematicians.VolII,EurMathSoc,Zürich,2006:151-190. [38]HUW,XICC.DerivedequivalencesandstableequivalencesofMoritatypeⅡ[OL].RevMatIberoam,Preprintavailableathttp://math0.bnu.edu.cn/~ccxi/. [39]CHENHX,XICC.Dominantdimensions,derivedequivalencesandtiltingmodules[J].IsrealJMath,2016,215(1):349-395. [40]FANGM,HUW,KOENIGS.Derivedequivalences,restrictiontoself-injectivesubalgebrasandinvarianceofhomologicaldimensions[OL].arXiv:1607.03513. [41]BRENNERS,BUTLERMCR.GeneralizationsoftheBernstein-Gelfand-Ponomarevreflectionfunctors[C]//Berlin:LectureNotesinMath,1980:103-169. [42]KERNERO,YAMAGATAK.Moritaalgebras[J].JAlgebra,2013,382(10):185-202. [43]BASSH.Finitisticdimensionandahomologicalgeneralizationofsemiprimaryrings[J].TransAmMathSoc,1960,95(3):466-488. [44]XICC. 关于有限维数猜想的一些进展[J]. 数学进展,2007,36(1):13-17. [45]TACHIKAWAH.Quasi-FrobeniusAlgebras[M].Heidelberg:Springer-Verlag,1971. [46]AUSLANDERM,REITENI.OnageneralizedversionoftheNakayamaconjecture[J].ProcAmMathSoc,1975,52(1):69-74. [47]COLBYRR,FULLERKR.AnoteontheNakayamaconjectures[J].TsukubaJMath,1990,14:343-352. [48]YAMAGATAK.Quasi-FrobeniusAlgebras[M]//HandbookofAlgebra,vol1.Amsterdam:North-Holland,1996:841-887.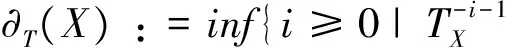
5 Nakayama猜想与其他同调猜想的联系

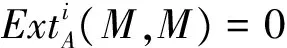


6 一些公开问题
