整体法在力学问题中的应用剖析

□江苏省南京市田家炳高级中学 耿若蕾

力学是物理知识体系的重要组成，也是高中物理的重要学习内容。在分析力学问题时存在一种关键的分析方法——整体法。运用整体法解题时将多个研究对象作为一个整体，忽略整个体系的内部因素，而重点分析体系的运动状态和外界条件对体系的影响，从而获得问题突破的关键条件。该方法在具体使用时同样离不开物理定律，有时也需要融合其它方法共同使用。合理利用该方法可以从研究对象的整体层面揭开其本质和规律。下面将深入剖析整体法的解题内涵，并结合考题从定律融合和方法融合角度剖析方法运用。

一、整体法的解题内涵

整体法是物理解题中广泛应用的一种思想方法，如力学问题中常涉及到众多的力和对象，利用整体法则可以避免对每个力的作用效果进行分析，而把研究对象看作是一个整体，只分析外力的作用效果，因此使用整体法可以把握问题的重点，降低思维难度。［1］

使用整体法求解力学问题时可以遵循一定的解题思路：首先确定研究目标，找准受力点，绘制受力图；然后将研究对象视为一个整体，针对性分析外力的作用，可以灵活变换研究对象；最后根据受力，考虑外界因素，结合力学规律，分析对象的运动状态，构建解题模型。

二、整体法的定律融合

整体法作为研究力学问题最为重要的思想方法之一，常与力学的重要定律相融合构建完整的研究体系，如牛顿运动定律、守恒定律等。解题时首先利用该方法的整体思想对研究对象进行力学分析，然后结合对应的定理分析整个研究体系，构建解题模型。［2］

1.与牛顿定律融合。

例1：右图所示的光滑水平面上有两个木块A和B，质量分别为m和M，两木块之间用轻绳相连接，且在水平向右的力F的作用下向右加速运动，若设两木块之间轻绳的张力为T，试求T的大小？

解析：首先将木块A和B看作是一个整体进行受力分析，如图（a）所示，根据牛顿第二定律可得F=（m+M）a，则然后单独分析木块A的受力，如图（b），可得T=ma，将上式代入则可得。

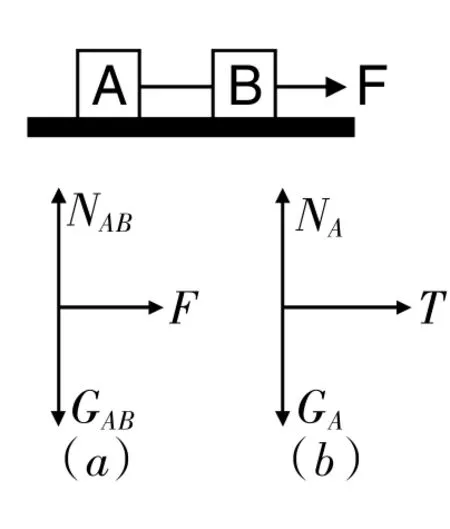
教学指导：在实际解题教学中，教师应首先指导学生理解整体法，然后指导学生忽略木块之间的作用力，将其作为研究对象的内力，并绘制整体研究对象的受力图，最后根据受力图，结合牛顿定律知识进行力学分析。

2.与守恒定理融合。

例2：右图所示，质量均为m的劈A和木块B位于光滑水平面上，物块B的左端固定着一个弹簧（质量忽略），现有一个质量也为m的小球C从劈A的弧面尖端静止释放，若释放点与水平面之间的高度为h，试求运动过程中弹簧的弹性势能所能达到的最大值？

解析：小球C从尖端释放后重力势能会转化为动能，然后与木块B相碰撞，从而压缩弹簧，同时使木块B向右运动，最终木块B和C以相同的速度运动，此时弹簧的弹性势能最大。上述运动过程可以分为小球C与劈A的分离和小球C与小球B碰撞两个过程，若将每个过程中的运动对象看作是一个整体，则每个体系均不受外力的影响，始终满足动量守恒和机械能守恒。

设小球C和劈A相分离时，小球C的速度为UO，劈A的速度为UA，若将两者看作是一个整体，由动量守恒可得mUO=mUA，由机械能守恒可得。小球C和木块B碰撞后弹簧的弹性势能最大时两者的速度相等，设为U，将两者看作是一个整体，则由动量守恒可得mUO=2mU ，由机械能守恒可得，综合两式可得弹性势能E p=mgh，则弹性势能所能达到的最大值为mgh。

教学指导：守恒定律的得出本身就是基于整体思想，因此在教学中有必要让学生回顾守恒定律的得出条件和研究过程，然后引导学生对整个运动过程进行分解，让学生思考每个过程的能量转化，并分析转化过程是否存在外力做功，是否有能量的损失，思考是否满足定律的使用条件。定律使用的关键一环就是对适用条件的分析，因此教学中需引导学生掌握定律解题的正确步骤。

三、整体法的方法融合

在实际解题中有时研究的对象和所受的力较多，使得整个研究体系过于复杂或抽象，此时就可以考虑采用多种方法相结合的方式，即实现整体法与其他方法的融合使用。在使用时可以根据具体的情形进行分步使用，也可以将两种方法相结合综合使用，与整体法相融合的常见方法有隔离法、等效法。［3］

1.与隔离法融合。

例3：右图所示的匀强电场中有两个带正电的小球A和B，两者均可以视为点电荷，位于同一竖直的直线上，在电场的作用下，两个小球会匀速下落且两球保持相同的距离，若小球A的质量为4m，电荷量为Q，小球B的质量为m，电荷量为4Q，试求两个小球下落时的距离和电场的场强大小？

解析：由于两个小球是匀速下落两者之间的距离保持不变，首先将两者看作是一个整体，竖直方向满足受力平衡，则有5mg=5QE，所以电场强度然后采用隔离法，对小球A进行受力分析，则小球受到自身的重力和场强力以及两个电荷之间的洛伦兹力，。教学指导：教学时应首先引导学生理解何为整体与隔离，然后指导学生辨析整体与隔离过程中所研究的力有何不同，在此基础上讲解两种方法融合解题的具体步骤。另外在解题结束后可以让学生思考何种情形下需要 采用整体与隔离的方法，引导学生明确求解多个对象之间的作用力或与对象作用力相关的物理量时需要结合隔离法，帮助学生在思想上建立隔离法使用的条件。

2.与等效法融合。

例4：右图所示的粗糙水平面上放置有一个三角形斜劈，质量为m0，且斜劈的两个斜面均为粗糙斜面，若在斜劈的左右粗糙斜面上分别放置质量为m1和m2的木块，则斜劈和木块m1仍然静止，而物块m2则沿斜劈加速下滑，加速度为a，试求水平面对斜劈的摩擦力和支持力？

解析：根据题干信息可知，斜劈和物块m1处于平衡状态，而物块m2存在沿斜面下滑的加速度，此时我们可以先将三者看作是一个整体，则可以将物块m2所受的加速度a等效转移到整个体系上，将物块m2的加速度a沿竖直方向和水平方向进行分解，如上图所示，则有ax=a cosθ2，ay=a sinθ2，则整体上体系有向右的加速力F=m2ax=ma cosθ2，但整个体系是没有移动的，故存在水平面对体系的摩擦力与加速力的平衡，即Ff=F，同时水平面对斜劈的摩擦力就为Ff，摩擦力的大小为ma cosθ2，方向为水平向左。

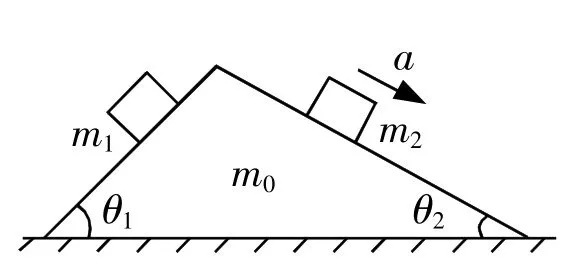
分析水平面对斜劈的支持力同样从整体上分析，竖直方向存在失重m2ay，水平面对斜劈的支持力就等于对整体体系的支持力，则FN=（m0+m1+m2）-ma sinθ2，方向为竖直向上。

教学指导：讲解整体法与等效法融合时，首先在思想上使学生理解整体法实质上就是对研究对象等效的过程，然后结合该题使学生理解加速度通过分解，也可以等效为力，从失重与超重角度对物理的状态进行等效，从而帮助学生掌握加速度分解的解题技巧。