漫谈多元函数最值问题的求解策略*

刘奕辰 郭建华(指导教师)

江苏省南京市第二十九中学高三(6)班 (210036)

在高三数学复习中，多元函数的最值问题是一种常见的题型，它常常融合函数、不等式、三角函数、解析几何等知识，一般具有综合性强，思维量大，技巧性强等特点，是学习中的一个难点.在学习过程中要不断反思、归纳和总结求解策略，以此探究解题规律，揭示解题方法，形成解题技能.

一、构造方程法

例1 设x，y为实数，若4x2+y2+xy=1，则2x+y的最大值为__________．

点评:由x，y为实数，将目标函数整体代换，即t=2x+y，把题设条件转化为关于变量t的一元二次方程，由于该方程有解，因此借助于其判别式求解.

二、基本不等式法

例2 在ΔABC中，角A，B，C所对的边分别为a，b，c，若a2+b2+2c2=8，则ΔABC面积的最大值为__________．

点评:由题设条件a2+b2+2c2=8的形式，以及求解的目标，自然想到用余弦定理，选择适当的形式再次表征三角形三边a，b，c间的数量关系，通过对a，b，c关系式的适当整合把三角形的面积表示成角C的三角函数，从而将多变量问题转化成单变量的函数最值问题，从而问题破解.

三、换元变换法

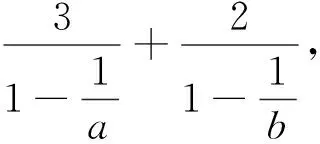
四、分离变量法

例4 若不等式x2-2y2≤cx(y-x)对任意满足x>y>0的实数x，y恒成立，则实数c的最大值为__________．

点评:变量分离法是高中数学解题的一种常规的、有效的方法，其实质是利用函数与方程的思想，将方程、不等式的有解及恒成立问题，转化为相应的函数的值域与最值问题.

五、变更主元法

点评:对于求解一类含参方程f(a,x)=0(a为参数)自变量x被限定在某个范围有解问题，如果从正面求解实数a的范围要面临很繁琐的讨论，那么就把a当做主元来求解，即令a=g(x)，转换为求函数a=g(x)关于自变量x的值域问题.即对于某些问题当利用主元难以求解时，可以考虑从次元出发(即化客为主)，并把主元放在次元的位置上进行处理，实施战略转移，其实它是一种换位法，体现了向对立面转化的特点.

六、待定系数法

例6 已知x,y,z∈(0,+∞)，且x2+y2+z2=1，则3xy+yz的最大值为__________．

点评:待定系数法待定系数法是指将目标多元代数式用条件中已有的多元代数式结合必要的待定系数表示出来，再按照一定的解题技巧求出待定系数，进而使目标求解.

七、数形结合法

<1)，且各件产品是否为不合格品相互独立．

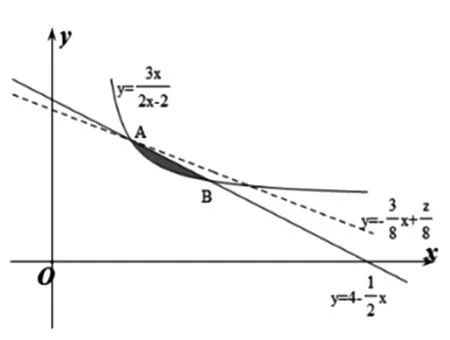
图1

点评:通过换元，联想其题设条件和目标函数所蕴含的几何意义，转换成线性规划问题，再借助于导数的几何意义求解目标最值.

因此，在以后的学习中对多元函数的最值问题，应采取多方位、多角度、多途径进行观察和思考，不断总结求解多元最值函数的方法和技巧，这些方法和技巧并不是孤立的，而是互相联系和渗透，因此要认真领悟每种方法背后的实质，才能达到举一反三，应用自如．