忽视最基本的方程函数思想，简单问题弄复杂

翁文建

贵州省毕节市梁才学校 (551700)

文[1][2][3]根据笛卡尔的方程理论，将所有数学问题归为方程的解集问题，将中学数学概括为三个“最基本”，即最基本的数学思想(方程函数思想)，最基本的数学方法(换、消元法)，最基本的解题思路(换元使问题进入方程组，消元让问题在一个方程中)，真正理解了这三个“最基本”，就有登上绝山顶，一览众山小的感觉，否则会把简单问题复杂化，下面以2017年重庆市一模冲刺预测卷理21第2小问的参考解答为例说明.

作为压轴题命题者的设计是难题，故参考解答也是按照难题解答给出的，为便于比较先录出参考解答

上述模拟题可以拓广到更一般的情况.

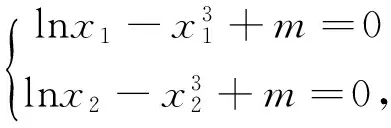
题2是当今比较流行的一类问题，还不时出现在高考题中，如2016年全国卷Ⅰ理(21)

已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.(Ⅰ)求a的取值范围；(Ⅱ)设x1,x2是f(x)的两个零点,证明：x1+x2<2.

另外还有一类可化为题2的一类问题，如2016年全国高考四川测试卷理10：设a,b是不相等的两个正数，且blna-alnb=a-b，给出下列结论

其中正确结论的序号是( ).

(A)①② (B)①③ (C)②③ (D)①②③

总之，问题的本质是不能解出的两个函数零点之和与极值点2倍的大小关系和两个函数零点之积与极值点平方的大小关系，当函数中的参数确定时，就不是变数问题，而是估计零点的近似值问题，用教科书中的零点判定法(二分法)就可比较简单的解决，且估计得越精确，得到的不等式越强，而用基本的方程函数思想审视中学数学教学，才能使中学数学教学自然，简单.

[1]熊福州.最基本的数学思想方法-方程思想，换元法，河北理科教学研究，2000年第4期.

[2]熊福州.换元让问题进入方程(组)，消元使问题在一个方程中，中学数学研究(江西)，2016年第12期.

[3]熊福州,张龙跃.数学问题的根基本质是方程的解集，中学数学研究(江西)，2015年第8期.