平面向量数量积求解高三微专题教学设计

王 炜

江苏省江阴市华士高级中学 (214421)

一、设计背景

我校均分3.18分，江阴市均分2.95分，成绩不够理想.平面向量数量积在高考中的能力要求较高，已经成为高考重点考查的知识.通过平面向量数量积的学习也可以提升学生的数学核心素养.以往的数学教学以“知识为本”，过渡到“以能力为本”，再发展到当前提出的“核心素养为本”.这是数学教学的渐进式发展的必然过程.“核心素养为本”要求课堂教学要从以往的“以教师的讲授为中心”转变为“以学生的自主探究为中心”.学生不仅要具备扎实的基础知识、基本方法和基本技能，而且要具备思维的整合与迁移能力，同时也要在情感态度和意志品质等方面获得全面的发展，从而促进学生数学核心素养的发展.

二、教学设计

1.昨夜西风凋碧树，独上高楼，望尽天涯路.

图1

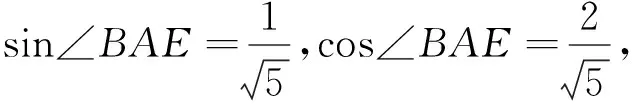
图2

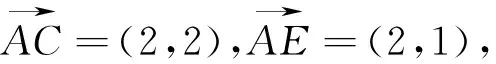
设计意图:引入平面向量数量积求解的三种途径.

2)礼花弹火药的特性：主要成分：高氯酸钾、六氯苯、碳酸锶、酚醛树脂、镁铝合金粉；烟花药剂点燃后，在燃烧过程中，原有的固体烯颗粒末完全反应和(或)反应生成新的固体可燃颗粒被火焰气流带出，和空气中的氧进行二次氧化反应、产生二次亮点而形成“喷波”效果。

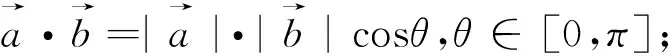
②转化法：转化为两个(几个)不共线的已知向量(基底)；

③坐标法.

教学建议:波利亚认为：“传统数学的缺点，在于往往口头讲解，而不是从实际操作开始数学教学”.通过“例1”，让学生动手实践，充分让学生展开思维碰撞，最终能够自我总结平面向量数量积求解的三种途径.在这一教学过程中，教师要更多地关注后进生的表现，“起步慢一点”对整节课课堂节奏的把握会更准确些.

2.衣带渐宽终不悔，为伊消得人憔悴.

图3

例2 如图3，AB是半圆O的直径，C、D是弧AB的三等分点，M、N是线段AB的三等分点.若OA=6，则

图4

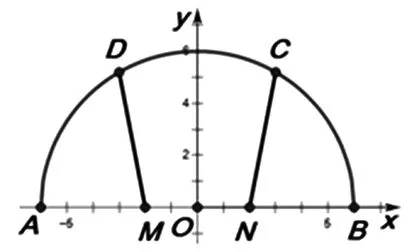
图5

设计意图:巩固平面向量数量积求解的三种途径，并初步感受不同解法的优劣(该题坐标法优于转化法，转化法优于定义法).

教学建议:相比较于“热身训练”，“例1”的难度明显加大.建构主义认为，学习时学生经验体系在一定环境中自内而外的“生长”，它是以学生原有的知识经验为基础实现知识的建构.因此，有了“例1”的铺垫，学生在“跳一跳才能够得着”的“例2”面前，通过个人独立思考，小组相互讨论和师生共同交流等形式，充分调动各方面的积极性，从而使每一个学生都能在原有的经验水平的基础上得到充分的发展.教师不能通过讲授法代替学生的思考，也不能直接提示该题取最优解法而不对其它方法进行探究与比较.所以，该题要留足时间，让学生深度思考，这样才能有效的进行知识迁移，从而切实培育数学核心素养.

图6

设计意图:尝试从不同途径(坐标法、转化法)解决平面向量数量积问题，获得数量积求解的成功体验.累积信心已成为数学学习过程中必须考虑的因素.如果我们的数学永远都是解不完的难题，对于大多数学生必然是一种打击，不利于数学的学习.

图7

设计意图:方法的比较，转化法(基底法)和坐标法实质是相同的，如果选取的两个基底互相垂直，用坐标法解题一般来说比较方便，如果基底不是互相垂直的，或者无法建立直角坐标系，则用转化法(基底法).故转化法适用于更为广泛的范围，坐标法适用范围小一些；如果能用坐标法，则优先选择坐标法，这样问题就转化为一些计算，少了一些思考.

3.众里寻他千百度，蓦然回首，那人却在灯火阑珊处.

图8

图9

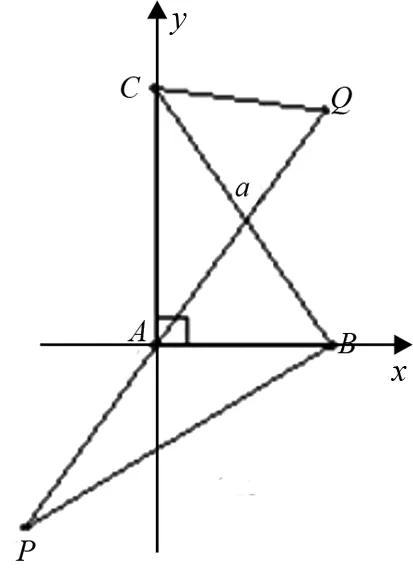
图10

设计意图:该题以解答题的形式出现，与之前所研究的题目的“风格”有明显的不同，难度进一步加大，试图通过该题的研究，真正掌握数量积求解之“道”(而不能停留在“术”的层面).

教学建议:学生普遍感觉“无从下手”，教师要正确引导学生进行审题.分析已知和目标，已知为解题提供了“可能性”，而目标为解题指明了“方法”，两者协同分析，再用通法就能解决.该题需要学生具备一定的分析问题的能力，不失为一道精彩的高考题.在高三复习中可以让学生适当接触，有利于学生方法的完善，能力的形成，分析问题能力的提升和意志品质的培养.

设计意图:经历了数量积求解的转化法和坐标法，特别是当我们有可能陷入题海时，回归定义很有必要，从而进一步巩固数量积求解的方法体系.

4.课堂小结

引导学生通过思维导图的形式总结本节课的内容：

三、教学反思

微专题是对传统专题的有机补充，它能够帮助学生将一个个孤立的知识点连接成系统的知识网络.微专题以“微”见大，操作性强、指向明确，可结合学科特点和学生的实际情况，适时穿插于传统专题的教学，避免低效的“炒冷饭”现象，从而切实提高教学效率.教育家苏霍姆林斯基说过：“没有自我教育，就不是真正的教育”.本节课始终在教师的引领下，学生对平面向量数量积进行深度学习，课堂上留足时间让学生自我反思，自我梳理，从而使学生获得结构化的数学核心知识，建立运用数学学科思想解决问题的思路方法，学生的创新精神、实践能力和科学精神得到充分的培养，从而使学生数学核心素养获得发展.

[1]曲文瑞,李学军.横看成岭侧成峰[J].中学数学教学参考,上旬,2014(8)：23-25.

[2]李宽珍.微专题教学方法的教学尝试[J].数学通讯,下半月,2017(1)：21-25.

[3]胡久华,宋晓敏.主题教学打通知识到素养的通道[N].中国教育报，2017.07.20第3版.